Non-injective functions map multiple inputs to the same output, leading to a lack of one-to-one correspondence between domain and codomain elements. Understanding their behavior is crucial in fields like cryptography, where collisions can affect security, and in mathematical analysis where function invertibility is examined. Explore the full article to learn how non-injective functions impact various applications and how to identify them.
Table of Comparison
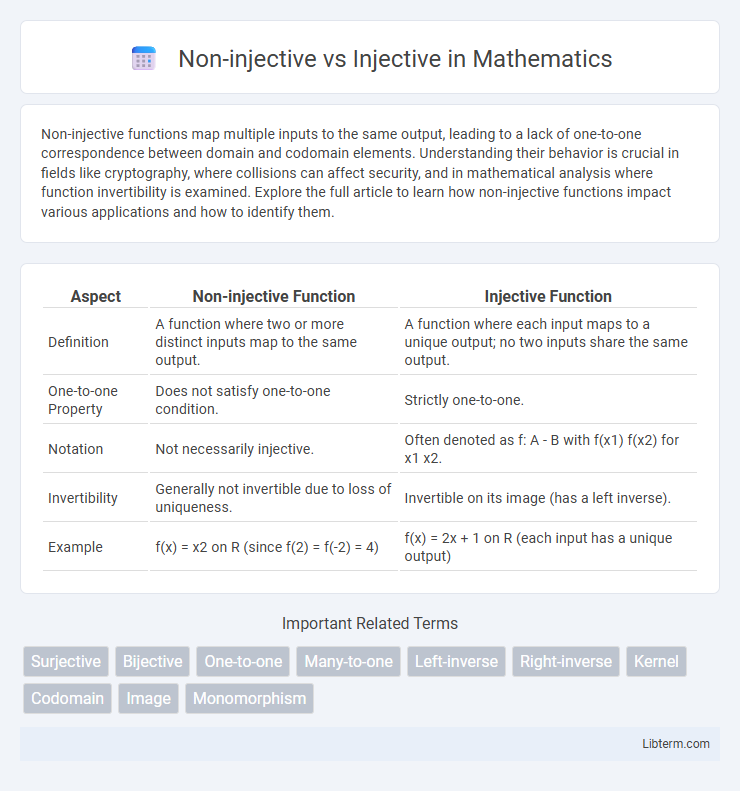
| Aspect | Non-injective Function | Injective Function |
|---|---|---|
| Definition | A function where two or more distinct inputs map to the same output. | A function where each input maps to a unique output; no two inputs share the same output. |
| One-to-one Property | Does not satisfy one-to-one condition. | Strictly one-to-one. |
| Notation | Not necessarily injective. | Often denoted as f: A - B with f(x1) f(x2) for x1 x2. |
| Invertibility | Generally not invertible due to loss of uniqueness. | Invertible on its image (has a left inverse). |
| Example | f(x) = x2 on R (since f(2) = f(-2) = 4) | f(x) = 2x + 1 on R (each input has a unique output) |
Understanding Injective Functions
An injective function, also known as a one-to-one function, maps each element of the domain to a distinct and unique element in the codomain, ensuring no two different inputs share the same output. Non-injective functions allow multiple inputs to map to the same output, leading to a loss of uniqueness and potential ambiguity in inverse mappings. Understanding injective functions is crucial in fields like algebra and computer science for ensuring reversible and well-defined transformations.
Exploring Non-injective Functions
Non-injective functions map at least two distinct elements from the domain to the same element in the codomain, resulting in a lack of one-to-one correspondence. These functions often appear in scenarios where multiple inputs produce identical outputs, such as in many-to-one mappings. Exploring non-injective functions highlights important concepts in mathematics and computer science, including equivalence relations and information loss.
Mathematical Definition: Injective vs Non-injective
An injective function, or one-to-one function, maps each element of the domain to a unique element in the codomain, ensuring no two distinct domain elements share the same image. A non-injective function fails this criterion by mapping at least two different domain elements to the same codomain element, thus lacking uniqueness. The mathematical definition of injectivity requires that for every pair of elements \(x_1, x_2\) in the domain, if \(f(x_1) = f(x_2)\), then \(x_1 = x_2\); non-injective functions violate this property.
Visualizing Function Relationships
Injective functions, or one-to-one mappings, visualize as curves where each x-value corresponds to a unique y-value, ensuring no horizontal line intersects the graph more than once. Non-injective functions fail this criterion, with at least one y-value linked to multiple x-values, causing horizontal line intersections at several points. Visualizing these differences highlights the distinct function behaviors, crucial for understanding mappings in mathematical analysis and application.
Key Differences Between Injective and Non-injective Mappings
Injective mappings assign each element of the domain to a unique element in the codomain, ensuring a one-to-one relationship without any repetitions. Non-injective mappings allow multiple elements of the domain to map to the same element in the codomain, resulting in a many-to-one relationship. The key difference lies in the uniqueness of codomain assignments: injective functions maintain distinct outputs for distinct inputs, while non-injective functions do not.
Examples of Injective Functions in Mathematics
An injective function, also known as a one-to-one function, maps each element of its domain to a unique element in its codomain, ensuring no two distinct inputs produce the same output. Common examples include the linear function f(x) = 2x + 3, where each input corresponds to a different output, and the exponential function f(x) = e^x, which is strictly increasing and injective over the real numbers. In contrast, non-injective functions, like f(x) = x^2, map multiple inputs to the same output, such as f(2) = f(-2) = 4, violating the one-to-one condition.
Real-world Applications of Non-injective Functions
Non-injective functions, where multiple inputs map to the same output, are crucial in real-world applications like data compression, cryptography, and neural networks, where information reduction or pattern recognition is needed. In encryption, non-injective mappings enable secure hash functions that condense data into fixed-size outputs despite input variability. Similarly, in machine learning, non-injective layers help neural networks generalize by mapping diverse input features to shared activations, enhancing model efficiency and performance.
Criteria for Identifying Function Types
A function is injective (one-to-one) if every element of the codomain is mapped by at most one element of the domain, ensuring no two distinct inputs share the same output. Non-injective functions fail this test by having at least two different domain elements mapped to the same codomain element. Identifying injectivity involves verifying that f(x1) = f(x2) implies x1 = x2 for all x1, x2 in the domain, often tested through algebraic manipulation or visual methods like the horizontal line test on graphs.
Importance of Injectivity in Mathematical Analysis
Injectivity ensures a one-to-one correspondence between elements in the domain and codomain, crucial for preserving distinct information in mathematical functions. This property enables the existence of inverse functions, which are fundamental in solving equations and analyzing functional behavior in mathematical analysis. Non-injective functions, lacking this uniqueness, can lead to ambiguous mappings, complicating the study of continuity, differentiability, and integrability.
Summary: When to Use Injective or Non-injective Functions
Injective functions are ideal when each element in the domain must map to a unique element in the codomain, ensuring no collisions and enabling reversible mappings. Non-injective functions are suitable when multiple inputs share the same output, such as in data compression or classification tasks where distinct inputs can produce identical results. Choosing between injective and non-injective functions depends on the need for uniqueness versus the allowance of shared outputs in the specific mathematical or computational context.
Non-injective Infographic
 libterm.com
libterm.com