Solving a quadratic equation involves finding the values of x that satisfy ax2 + bx + c = 0, where a, b, and c are constants. The most common methods include factoring, completing the square, and using the quadratic formula, each providing a systematic approach to identifying the roots. Explore the rest of this article to master these techniques and confidently solve any quadratic equation you encounter.
Table of Comparison
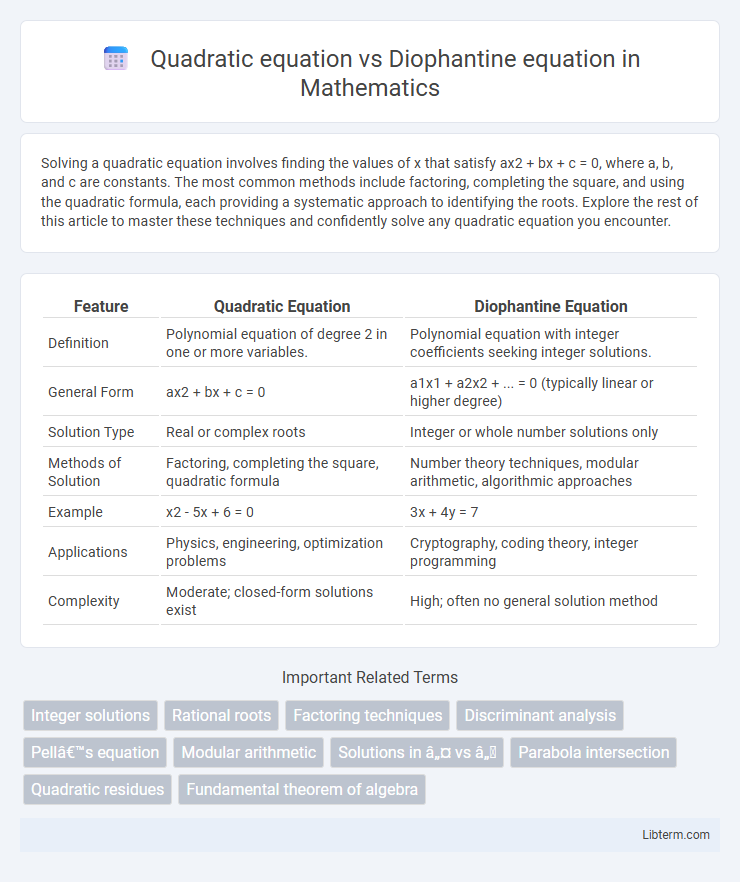
| Feature | Quadratic Equation | Diophantine Equation |
|---|---|---|
| Definition | Polynomial equation of degree 2 in one or more variables. | Polynomial equation with integer coefficients seeking integer solutions. |
| General Form | ax2 + bx + c = 0 | a1x1 + a2x2 + ... = 0 (typically linear or higher degree) |
| Solution Type | Real or complex roots | Integer or whole number solutions only |
| Methods of Solution | Factoring, completing the square, quadratic formula | Number theory techniques, modular arithmetic, algorithmic approaches |
| Example | x2 - 5x + 6 = 0 | 3x + 4y = 7 |
| Applications | Physics, engineering, optimization problems | Cryptography, coding theory, integer programming |
| Complexity | Moderate; closed-form solutions exist | High; often no general solution method |
Introduction to Quadratic and Diophantine Equations
Quadratic equations are polynomial equations of degree two, represented as ax2 + bx + c = 0, where a, b, and c are real or complex coefficients. Diophantine equations involve finding integer solutions to polynomial equations, often with multiple variables and constraints, named after the ancient mathematician Diophantus. Understanding the fundamental differences between quadratic and Diophantine equations is crucial for solving problems in algebra, number theory, and cryptography.
Defining Quadratic Equations: Key Concepts
Quadratic equations are polynomial equations of the form ax2 + bx + c = 0, where a, b, and c are constants with a 0, and solutions are found using methods like factoring, completing the square, or the quadratic formula. These equations often yield real or complex roots, distinguishing them from Diophantine equations that seek integer solutions exclusively. Understanding the nature of coefficients and solution sets is essential for solving quadratic equations and differentiating them from integer-based Diophantine problems.
Exploring Diophantine Equations: An Overview
Diophantine equations involve finding integer solutions to polynomial equations, contrasting with quadratic equations that typically focus on real or complex roots. These equations often require advanced number theory techniques, such as modular arithmetic and the theory of elliptic curves, to explore their solvability. Understanding Diophantine equations enables deeper insights into integer solutions and their applications across cryptography and algebraic geometry.
Types of Solutions: Real vs Integer Approaches
Quadratic equations typically yield real or complex number solutions derived via methods like the quadratic formula or completing the square, focusing on continuous solution sets. Diophantine equations, conversely, demand integer solutions, often requiring techniques such as modular arithmetic, the Euclidean algorithm, or lattice-based methods to identify precise integer values satisfying the equation. The fundamental distinction lies in quadratic equations addressing real-valued roots, whereas Diophantine equations emphasize integral or whole-number solutions within number theory.
Methods of Solving Quadratic Equations
Methods of solving quadratic equations include factoring, completing the square, using the quadratic formula, and graphing. Factoring involves expressing the quadratic as a product of binomials, while completing the square rewrites the equation into a perfect square trinomial. The quadratic formula, derived from the standard form ax2 + bx + c = 0, provides exact solutions by calculating roots using the discriminant (b2 - 4ac).
Techniques for Solving Diophantine Equations
Techniques for solving Diophantine equations often involve methods such as modular arithmetic, the use of the Euclidean algorithm, and factorization strategies tailored to integer solutions. Unlike quadratic equations, which primarily rely on algebraic formulas and the quadratic formula for real or complex roots, Diophantine equations require integer-specific approaches like the method of infinite descent or the application of Pell's equation solutions. Advanced strategies include lattice basis reduction and leveraging number theory concepts such as congruences and prime factorization to identify integer solutions effectively.
Applications in Real-World Problems
Quadratic equations are widely used in physics and engineering to model projectile motion, optimization problems, and structural design due to their ability to describe parabolic trajectories and relationships involving squared variables. Diophantine equations, characterized by integer solutions, are essential in cryptography, coding theory, and integer-based scheduling problems where discrete values are crucial. Both equations provide foundational mathematical tools for solving real-world problems that require continuous versus discrete solution sets, respectively.
Historical Development and Mathematical Importance
Quadratic equations, dating back to ancient Babylonian mathematics around 2000 BCE, represent some of the earliest algebraic problem-solving methods, crucial for the development of algebra and calculus. Diophantine equations, named after Diophantus of Alexandria in the 3rd century CE, form a foundational branch of number theory, focusing on integer solutions and influencing modern cryptography and algorithm design. The historical progression from quadratic equations to Diophantine analysis highlights the evolution from general polynomial solving to specialized integer solution problems with profound implications in both theoretical and applied mathematics.
Key Differences Between Quadratic and Diophantine Equations
Quadratic equations involve polynomial expressions of degree two, typically represented as ax2 + bx + c = 0, with solutions often found in real or complex numbers. Diophantine equations require integer solutions and can include linear, quadratic, or higher-degree polynomials, making their solution sets more restrictive and complex. The key difference lies in the solution domain--quadratic equations allow continuous values, while Diophantine equations demand discrete integer solutions, significantly affecting their solvability and methods used.
Conclusion: Comparing Quadratic and Diophantine Equations
Quadratic equations involve polynomial expressions of degree two and typically yield real or complex solutions, essential in fields like algebra and calculus. Diophantine equations require integer solutions, posing significant challenges due to their discrete nature and applications in number theory and cryptography. Understanding the fundamental differences highlights that quadratic equations are versatile for continuous analysis, while Diophantine equations emphasize integer constraints, impacting problem-solving approaches and computational complexity.
Quadratic equation Infographic
 libterm.com
libterm.com