Arc length measures the distance along a curved line between two points, essential in geometry and calculus for understanding curve dimensions. Calculating arc length involves integrating the square root of the sum of squared derivatives, providing precise results for irregular curves. Explore this article to master the formulas and techniques for determining arc length in various contexts.
Table of Comparison
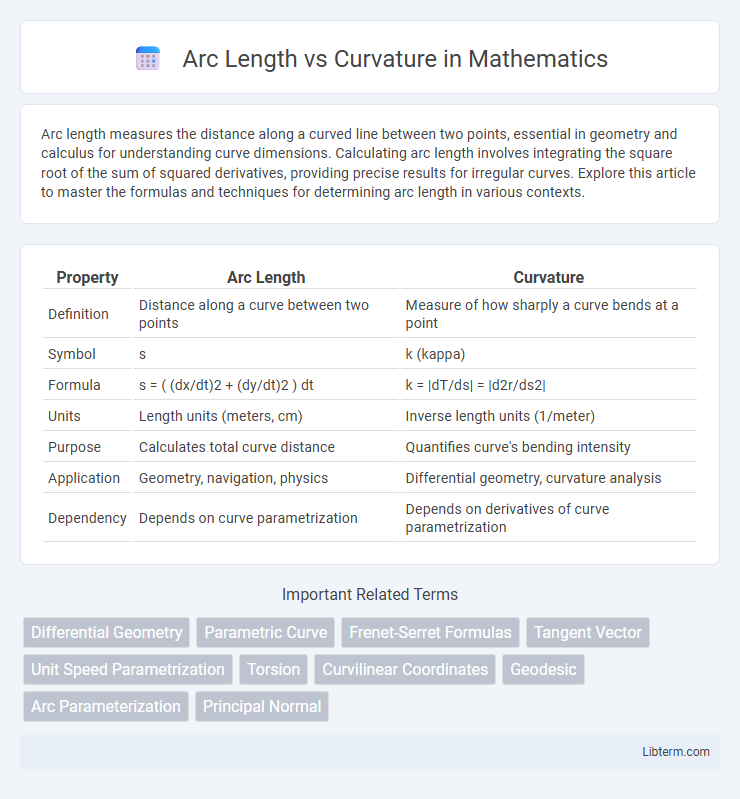
| Property | Arc Length | Curvature |
|---|---|---|
| Definition | Distance along a curve between two points | Measure of how sharply a curve bends at a point |
| Symbol | s | k (kappa) |
| Formula | s = ( (dx/dt)2 + (dy/dt)2 ) dt | k = |dT/ds| = |d2r/ds2| |
| Units | Length units (meters, cm) | Inverse length units (1/meter) |
| Purpose | Calculates total curve distance | Quantifies curve's bending intensity |
| Application | Geometry, navigation, physics | Differential geometry, curvature analysis |
| Dependency | Depends on curve parametrization | Depends on derivatives of curve parametrization |
Introduction to Arc Length and Curvature
Arc length measures the distance along a curve between two points, serving as a fundamental tool in geometry and calculus for quantifying the actual length of curved shapes. Curvature quantifies how sharply a curve bends at a given point, defined mathematically as the rate of change of the tangent angle with respect to arc length. Understanding the relationship between arc length and curvature is essential for applications in physics, engineering, and computer graphics, where precision in describing curve properties influences design and analysis.
Defining Arc Length in Geometry
Arc length in geometry measures the distance along a curve, calculated by integrating the square root of the sum of the derivatives of the curve's parametric equations squared. It provides a precise quantitative value representing the length of a curve segment between two points, essential for understanding geometric properties and physical applications. Arc length is distinct from curvature, which quantifies how sharply a curve bends at a given point rather than the total distance along the curve.
Understanding Curvature in Curves
Curvature measures how sharply a curve bends at a given point, defined as the rate of change of the tangent direction with respect to arc length. Analyzing curvature provides insight into the local geometric properties of curves, with higher curvature indicating tighter bending and lower curvature corresponding to nearly straight segments. Understanding curvature is essential for applications in physics, computer graphics, and differential geometry, enabling precise modeling of natural and engineered shapes.
Mathematical Formulas for Arc Length
Arc length \( s \) of a curve defined by a function \( y = f(x) \) over the interval \([a, b]\) is calculated by the integral \( s = \int_a^b \sqrt{1 + \left(\frac{dy}{dx}\right)^2} \, dx \). For parametric curves \( x = x(t), y = y(t) \), the arc length from \( t = \alpha \) to \( t = \beta \) is given by \( s = \int_\alpha^\beta \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} \, dt \). Curvature \( \kappa \), which measures the rate of change of the tangent vector with respect to arc length, is related but distinct from arc length, often expressed as \( \kappa = \frac{d\theta}{ds} \) where \( \theta \) is the tangent angle.
Mathematical Representation of Curvature
Curvature (\( \kappa \)) quantifies how sharply a curve bends at a given point, mathematically expressed as \( \kappa = \frac{|d\mathbf{T}/ds|}{|ds|} \), where \(\mathbf{T}\) is the unit tangent vector and \(s\) is the arc length parameter. This intrinsic measure depends on the second derivative of the curve's position vector with respect to arc length, linking curvature directly to the rate of change of the tangent vector. Unlike arc length, which measures the distance along the curve, curvature captures the geometric deviation from a straight path and is crucial in fields such as differential geometry and motion analysis.
Arc Length vs Curvature: Key Differences
Arc length measures the distance along a curve between two points, representing the total length traversed, while curvature quantifies how sharply the curve bends at a specific point, indicating the rate of change of the tangent direction. Arc length is a scalar value integral to describing the extent of the curve, whereas curvature is a local geometric property defined as the magnitude of the derivative of the unit tangent vector with respect to arc length. Understanding the distinction between arc length and curvature is crucial in applications such as differential geometry, computer graphics, and motion planning for accurately characterizing curve shapes and navigational paths.
Applications of Arc Length in Science and Engineering
Arc length plays a critical role in physics for calculating displacement along curved paths and in engineering for designing precise components like gears and bridges. In computer graphics, accurate arc length parametrization ensures realistic animations and curves rendering. Biomedical engineering uses arc length to model anatomical structures and analyze motion trajectories in biomechanics.
Real-World Uses of Curvature
Curvature quantifies how sharply a curve bends, informing critical applications like road design to ensure safe, navigable turns and in computer graphics for smooth rendering of 3D models. Arc length measures the distance along a curve, essential for calculating travel paths and material lengths, but curvature directly impacts structural integrity assessments in engineering by identifying stress concentration points. Understanding curvature enables advancements in robotics for precise movement, medical imaging for accurate anatomical mapping, and geospatial analysis in terrain evaluation.
Relationship Between Arc Length and Curvature
The relationship between arc length and curvature is fundamental in differential geometry, where curvature measures how sharply a curve bends at a given point along its arc length parameterization. Curvature is defined as the rate of change of the unit tangent vector with respect to arc length, making arc length the natural parameter for describing curvature. Precisely, for a plane curve parameterized by arc length \( s \), curvature \( \kappa(s) \) equals \( \left| \frac{d\mathbf{T}}{ds} \right| \), where \( \mathbf{T} \) is the unit tangent vector.
Summary: Choosing Between Arc Length and Curvature
Arc length measures the distance along a curve, providing a direct quantification of shape size, while curvature quantifies how sharply the curve bends at each point, revealing geometric properties independent of length. Selecting between arc length and curvature depends on analysis goals: arc length suits applications needing total path distance, whereas curvature is essential for understanding shape behavior, flexibility, or smoothness. Optimal use involves leveraging arc length for global dimensional context and curvature for local geometric insights in curve modeling or shape analysis.
Arc Length Infographic
 libterm.com
libterm.com