Elements in a periodic group share similar chemical properties due to having the same number of valence electrons, influencing their reactivity and bonding patterns. Understanding these groups helps predict element behavior in chemical reactions and material properties. Explore the rest of the article to discover how periodic groups shape the structure of the periodic table and impact your study of chemistry.
Table of Comparison
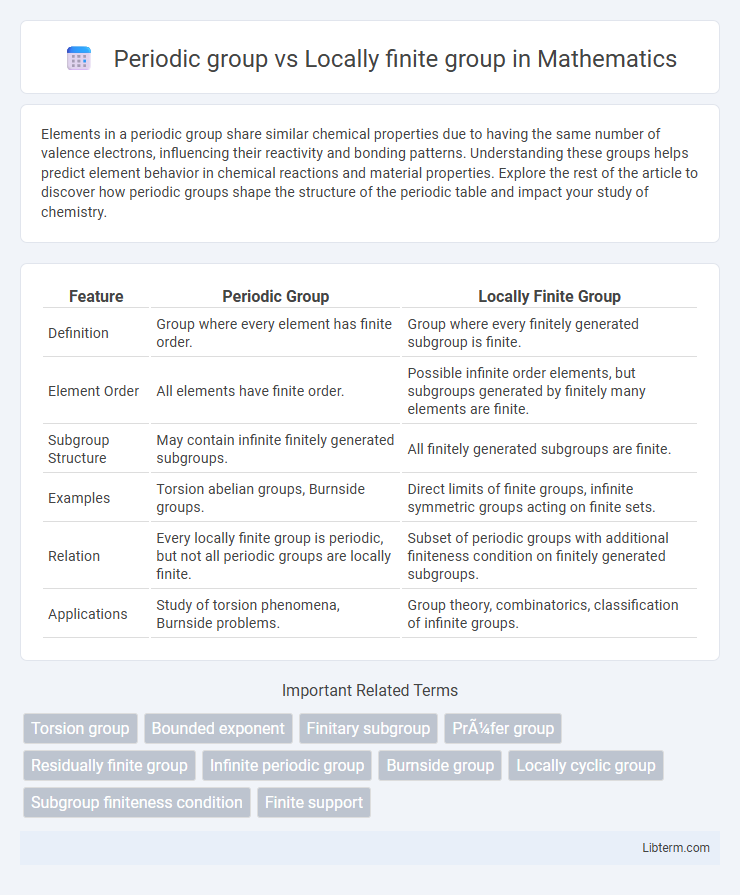
| Feature | Periodic Group | Locally Finite Group |
|---|---|---|
| Definition | Group where every element has finite order. | Group where every finitely generated subgroup is finite. |
| Element Order | All elements have finite order. | Possible infinite order elements, but subgroups generated by finitely many elements are finite. |
| Subgroup Structure | May contain infinite finitely generated subgroups. | All finitely generated subgroups are finite. |
| Examples | Torsion abelian groups, Burnside groups. | Direct limits of finite groups, infinite symmetric groups acting on finite sets. |
| Relation | Every locally finite group is periodic, but not all periodic groups are locally finite. | Subset of periodic groups with additional finiteness condition on finitely generated subgroups. |
| Applications | Study of torsion phenomena, Burnside problems. | Group theory, combinatorics, classification of infinite groups. |
Introduction to Periodic and Locally Finite Groups
Periodic groups are algebraic structures where every element has finite order, meaning each element generates a finite cyclic subgroup. Locally finite groups extend this concept by ensuring every finitely generated subgroup is finite, which implies a more stringent local finiteness condition beyond individual elements. These foundational distinctions underpin studies in group theory related to finiteness properties and structural behaviors of infinite groups.
Defining Periodic Groups
Periodic groups consist of elements with finite order, meaning every element in the group generates a finite cyclic subgroup. Unlike locally finite groups, which require every finitely generated subgroup to be finite, periodic groups emphasize the boundedness of individual elements' orders without necessarily constraining subgroup finiteness. This distinction highlights that all locally finite groups are periodic, but the converse is not always true, reflecting differing structural properties within group theory.
Understanding Locally Finite Groups
Locally finite groups are characterized by every finitely generated subgroup being finite, distinguishing them from general periodic groups where all elements have finite order but the structure might not be locally finite. Understanding locally finite groups involves analyzing their finite subgroups and how they integrate into the larger infinite group. This insight aids in exploring group actions, subgroup classifications, and applications in algebraic and geometric contexts.
Key Differences Between Periodic and Locally Finite Groups
Periodic groups consist entirely of elements with finite order, meaning every element generates a finite cyclic subgroup. Locally finite groups extend this notion by requiring that every finitely generated subgroup is finite, which implies periodicity but also allows for infinite overall group size. The key difference lies in the global structure: periodic groups emphasize element-wise finite order, while locally finite groups emphasize finiteness at the level of finitely generated subgroups.
Examples of Periodic Groups
Periodic groups, also known as torsion groups, consist entirely of elements with finite order, exemplified by finite cyclic groups such as \( \mathbb{Z}/n\mathbb{Z} \), the Prufer \(p\)-groups \( \mathbb{Z}(p^\infty) \), and finite symmetric groups \( S_n \). In contrast, locally finite groups are groups in which every finitely generated subgroup is finite; periodic groups like infinite direct sums of cyclic groups \( \bigoplus_{i \in I} \mathbb{Z}/p\mathbb{Z} \) are common examples that are also locally finite. These examples highlight that while all locally finite groups are periodic, periodic groups need not be locally finite unless additional structural conditions are met.
Examples of Locally Finite Groups
Locally finite groups are groups in which every finitely generated subgroup is finite, such as the additive group of rational numbers with denominators restricted to powers of a prime or direct limits of finite groups like the infinite direct sum of cyclic groups of order p. Periodic groups, where every element has finite order, include examples like the quasicyclic p-groups, but unlike locally finite groups, periodic groups need not have all finitely generated subgroups finite. The Burnside groups of bounded exponent, generated by finite sets and with elements of finite order, provide examples illustrating distinctions between periodicity and local finiteness in group theory.
Structural Properties and Subgroup Behavior
Periodic groups consist entirely of elements with finite order, ensuring every subgroup inherits periodicity, which often leads to constraints on possible group structures, such as limitations on torsion-free components. Locally finite groups are characterized by every finitely generated subgroup being finite, implying that these groups exhibit highly controlled subgroup behavior, facilitating a decomposition into finite building blocks and often allowing classification through direct limits of finite groups. The structural properties differ as periodic groups may contain infinite subgroups with complex interactions, while locally finite groups guarantee finiteness at the local level, ensuring subgroup closure and stability under finite generation.
Applications in Group Theory and Algebra
Periodic groups, where every element has finite order, are crucial in classifying torsion phenomena in group theory and aid in understanding the structure of infinite groups through Burnside-type problems. Locally finite groups, characterized by every finitely generated subgroup being finite, find applications in constructing and analyzing groups that bridge finite and infinite cases, particularly in module theory and representation theory. Both classes play significant roles in algebra by providing frameworks for exploring group actions, automorphism groups, and stability properties in infinite group contexts.
Historical Development and Key Theorems
The historical development of periodic groups traces back to Burnside's problem posed in 1902, questioning whether finitely generated periodic groups must be finite, inspiring extensive research on infinite periodic groups. Locally finite groups gained significant attention through the works of Philip Hall and B. H. Neumann in the mid-20th century, focusing on groups in which every finitely generated subgroup is finite, contributing critical structural insights. Key theorems include Burnside's theorem for periodic groups, establishing finiteness under specific conditions, and Hall-Kulatilaka's theorem, which asserts the existence of infinite finitely generated locally finite groups, highlighting fundamental differences between these two classes.
Open Questions and Future Research Directions
Open questions in the study of periodic groups versus locally finite groups prominently include the characterization of the extent to which locally finite groups exhibit behaviors identical to periodic groups and the classification of infinite periodic groups that are not locally finite. Future research directions aim to explore the mechanisms governing the growth and structure of periodic subgroups within locally finite groups, as well as the role of torsion elements in determining group properties. Advances in these areas may provide deeper insights into group theory, particularly in understanding subgroup lattice structures and applications to algebraic and geometric contexts.
Periodic group Infographic
 libterm.com
libterm.com