A pullback is a temporary reversal in the price of an asset within an ongoing trend, often seen as a healthy pause before the trend continues. Traders use pullbacks to identify potential entry points by analyzing support levels and market momentum. Explore the rest of the article to understand how to effectively spot and capitalize on pullbacks in your trading strategy.
Table of Comparison
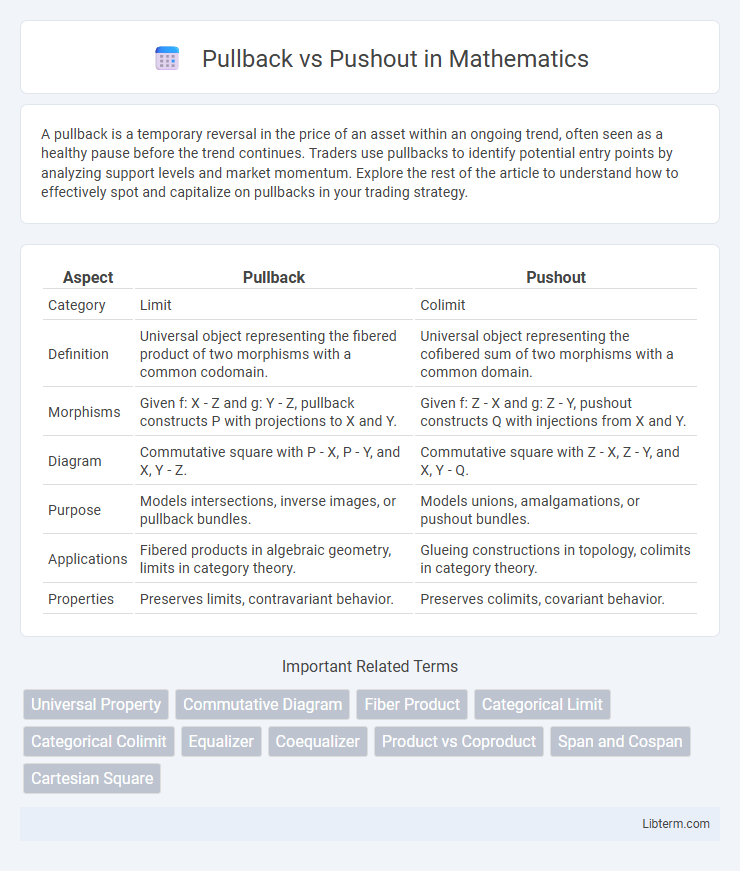
| Aspect | Pullback | Pushout |
|---|---|---|
| Category | Limit | Colimit |
| Definition | Universal object representing the fibered product of two morphisms with a common codomain. | Universal object representing the cofibered sum of two morphisms with a common domain. |
| Morphisms | Given f: X - Z and g: Y - Z, pullback constructs P with projections to X and Y. | Given f: Z - X and g: Z - Y, pushout constructs Q with injections from X and Y. |
| Diagram | Commutative square with P - X, P - Y, and X, Y - Z. | Commutative square with Z - X, Z - Y, and X, Y - Q. |
| Purpose | Models intersections, inverse images, or pullback bundles. | Models unions, amalgamations, or pushout bundles. |
| Applications | Fibered products in algebraic geometry, limits in category theory. | Glueing constructions in topology, colimits in category theory. |
| Properties | Preserves limits, contravariant behavior. | Preserves colimits, covariant behavior. |
Introduction to Pullback and Pushout Concepts
Pullback and pushout are fundamental concepts in category theory used to describe universal constructions involving objects and morphisms. A pullback represents a limit, capturing a "fibered product" of two morphisms with a common codomain, ensuring the most general object mapping into both simultaneously. Conversely, a pushout is a colimit, creating a "cofibered sum" by unifying two morphisms with a common domain, forming the most general object receiving maps from both.
Fundamental Definitions
Pullbacks in category theory represent the limit of two morphisms with a common codomain, generalizing the notion of a fibered product by capturing their universal property with an object and morphisms making a commutative square. Pushouts, dually, are colimits of two morphisms with a common domain, constructing a universal object by "gluing" along shared subobjects, encapsulating cocone properties in a commutative diagram. Both structures serve foundational roles in algebraic topology, algebraic geometry, and homological algebra by formalizing intersections and unions within categorical contexts.
Visualizing Pullback and Pushout
Visualizing pullback involves identifying the universal object that maps into two given objects along specified morphisms, often represented as a commutative square in category theory. In contrast, the pushout represents the universal object receiving morphisms from two objects sharing a common subobject, depicted as a dual commutative square where objects are merged. These visualizations aid in understanding limits and colimits, highlighting how pullbacks correspond to intersections or fibered products, while pushouts correspond to unions or amalgamations within categories.
Key Differences Between Pullback and Pushout
Pullback and pushout are fundamental constructions in category theory used to define limits and colimits, respectively. A pullback captures the universal property of a product combined with equalizers, often representing the "fibered" intersection of objects over a common codomain, while a pushout models the universal amalgamation or "gluing" of objects along a shared subobject. The key difference lies in their universal properties: pullbacks deal with cones under a diagram seeking the greatest lower bound, whereas pushouts pertain to cocones over a diagram identifying the least upper bound.
Practical Applications in Mathematics
Pullbacks and pushouts serve as fundamental constructions in category theory, facilitating the analysis of limits and colimits in diverse mathematical contexts. Pullbacks model the intersection of structures such as fibered products in algebraic geometry and solution sets in logic, while pushouts capture the process of gluing spaces or algebraic objects together, essential in topology and homological algebra. These tools enable mathematicians to systematically manage complex diagrams and universal properties, streamlining proofs and computations in fields like sheaf theory, group extensions, and cohomology.
Examples in Category Theory
Pullbacks illustrate the limit construction representing the universal object mapping to two objects with a shared morphism, often visualized in sets as the fiber product where elements pair up over a common target. Pushouts serve as colimits, uniting two objects by identifying shared substructures, exemplified in topological spaces by gluing spaces along a common subspace. In diagrammatic terms, pullbacks form a commutative square that is universal for cones into two objects, while pushouts form universal cocones merging two objects over a shared domain.
Pullback in Everyday Problem Solving
Pullbacks in everyday problem solving help unify data from different sources by identifying commonalities, such as merging customer information from multiple databases based on shared identifiers. This categorical concept ensures consistency when reconciling overlapping data sets, enabling accurate integration and comparison. In contrast, pushouts combine structures by uniting along shared parts, typically used for constructing new composite objects rather than aligning existing data.
Pushout in Real-World Contexts
Pushouts in real-world contexts model the merging of data or systems by identifying and unifying shared components, such as integrating different database schemas with overlapping tables. This categorical concept facilitates collaborative workflows by enabling consistent composition of processes, software modules, and network topologies through coalescing common interfaces. Applications in urban planning and robotics leverage pushouts to merge maps or sensor inputs, ensuring coherent assembly of partial information into unified frameworks.
Common Mistakes and Misconceptions
Pullback and pushout are often confused due to their dual nature in category theory, but a common mistake is treating them interchangeably without considering their distinct universal properties. Misconceptions arise when learners assume pullbacks always represent limits and pushouts always represent colimits without verifying specific diagram contexts. Another frequent error is overlooking the directionality of morphisms, leading to incorrect diagram constructions and flawed conclusions in applications like fiber products or coproducts.
Conclusion and Further Reading
Pullback and pushout constructions in category theory serve as fundamental dual concepts for universal mapping properties, with pullbacks characterizing limit objects and pushouts exemplifying colimit objects. Their applications span diverse mathematical fields such as topology, algebra, and logic, often facilitating the construction of fibered products and amalgamated sums, respectively. For comprehensive exploration, references include Mac Lane's "Categories for the Working Mathematician," Awodey's "Category Theory," and detailed articles in the nLab and the Stanford Encyclopedia of Philosophy.
Pullback Infographic
 libterm.com
libterm.com