A sphere is a perfectly round three-dimensional shape where every point on its surface is equidistant from the center. Its geometric properties make it fundamental in fields such as mathematics, physics, and engineering. Explore the article to understand how spheres influence science and everyday applications.
Table of Comparison
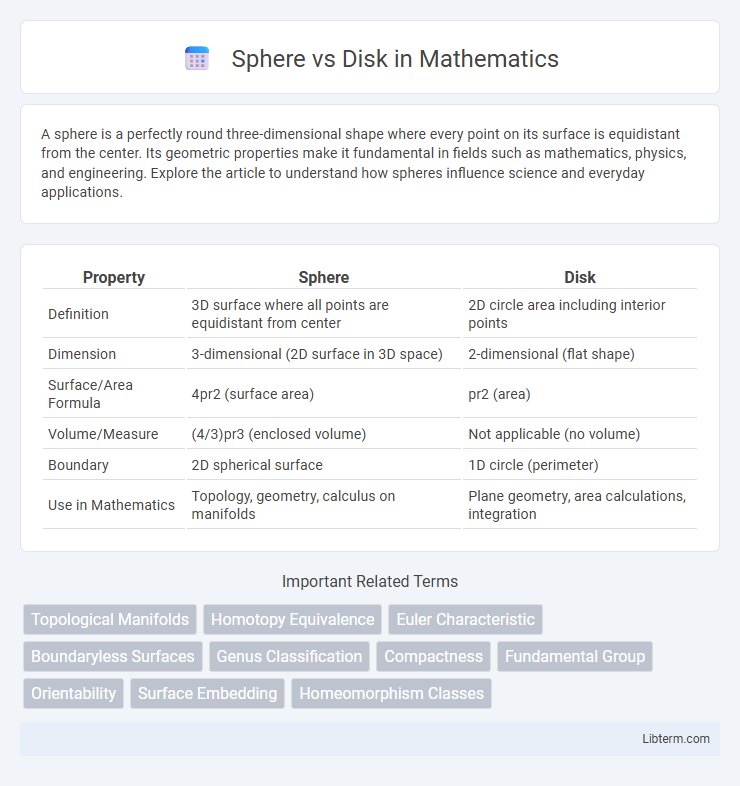
| Property | Sphere | Disk |
|---|---|---|
| Definition | 3D surface where all points are equidistant from center | 2D circle area including interior points |
| Dimension | 3-dimensional (2D surface in 3D space) | 2-dimensional (flat shape) |
| Surface/Area Formula | 4pr2 (surface area) | pr2 (area) |
| Volume/Measure | (4/3)pr3 (enclosed volume) | Not applicable (no volume) |
| Boundary | 2D spherical surface | 1D circle (perimeter) |
| Use in Mathematics | Topology, geometry, calculus on manifolds | Plane geometry, area calculations, integration |
Introduction to Spheres and Disks
Spheres and disks are fundamental geometric shapes used in various scientific and mathematical contexts; a sphere is a perfectly round 3D object where every point on the surface is equidistant from the center, while a disk is a flat, 2D circular region bounded by a circumference. In topology and geometry, spheres represent closed surfaces with constant curvature, essential in studying spatial properties and dimensions. Disks serve as basic planar shapes used in computer graphics, calculus, and physics to model circular areas and surfaces.
Geometric Definitions and Key Differences
A sphere is a three-dimensional geometric object defined as the set of all points equidistant from a fixed center point in space, characterized by a radius and surface area calculated as 4pr2. A disk is a two-dimensional figure consisting of all points within a circle, including the boundary, with area pr2 and lying flat on a plane. The key difference lies in dimensionality: spheres encompass volume and surface in 3D space, while disks are flat shapes confined to 2D planes.
Volume and Surface Area Comparisons
A sphere's volume is calculated by the formula \( V = \frac{4}{3} \pi r^3 \), while a disk, essentially a cylinder with negligible height, has volume \( V = \pi r^2 h \), often approaching zero when height is minimal. The surface area of a sphere is \( A = 4 \pi r^2 \), encompassing its entire curved surface, whereas a disk's surface area is dominated by its two flat circular faces, each \( \pi r^2 \), plus the area of the side if it has thickness. Comparing these, spheres maximize enclosed volume relative to surface area, making them highly efficient shapes in nature and engineering.
Mathematical Equations: Sphere vs Disk
The mathematical equation of a sphere is defined as \( x^2 + y^2 + z^2 = r^2 \), representing all points in three-dimensional space at a fixed radius \( r \) from the center. In contrast, the equation for a disk lies in two dimensions, typically expressed as \( x^2 + y^2 \leq r^2 \), which represents all points within or on the boundary of a circle with radius \( r \). The sphere equation involves three variables, reflecting volume in 3D space, while the disk equation restricts to a planar region, reflecting area in 2D space.
Applications in Science and Engineering
Spheres are widely utilized in physics and engineering for modeling particles, celestial bodies, and fluid dynamics due to their symmetric properties and minimal surface area for a given volume. Disks find prevalent applications in electronics, optics, and material science, serving as fundamental components in hard drives, lenses, and thin films where surface area and planar geometry are critical. The choice between spheres and disks depends on the specific requirements of spatial symmetry, surface interaction, and volume efficiency in scientific simulations and engineering designs.
Physical Properties: Strength and Stability
Spheres exhibit superior strength and stability compared to disks due to their uniform distribution of stress across the surface, minimizing weak points and enhancing load-bearing capacity. In contrast, disks experience uneven stress distribution, especially around edges, which can lead to higher chances of deformation or failure under pressure. This structural efficiency makes spheres ideal for applications requiring durability and resistance to external forces.
Visualizing Spheres and Disks
Visualizing spheres involves rendering three-dimensional surfaces defined by all points equidistant from a center, emphasizing curvature and depth through shading and perspective techniques. Disks are visualized as two-dimensional circular regions or flat surfaces bounded by a single radius, often highlighted by their planar nature and uniform shading. Employing advanced graphics algorithms like ray tracing for spheres and rasterization for disks enhances the realistic depiction of these geometric entities in computer graphics.
Real-World Examples
Spheres appear in real-world objects such as basketballs, planets, and bubbles, showcasing their perfect symmetry and volume efficiency in three dimensions. Disks are common in items like coins, CDs, and pizza slices, representing flat, two-dimensional circular shapes with consistent thickness. Understanding the differences between spheres and disks helps optimize design and functionality in fields like manufacturing, astronomy, and everyday objects.
Pros and Cons of Spheres vs Disks
Spheres offer uniform geometry with equal curvature in all directions, providing optimal volume-to-surface-area ratio, which enhances strength and minimizes surface energy. Disks provide structural advantages in applications requiring flat surfaces, ease of stacking, and efficient use of space, especially in storage or data representation contexts. Spheres may incur higher manufacturing costs and complex handling due to their shape, while disks can suffer from edge wear and reduced strength under multi-directional stress.
Conclusion: Choosing Between Sphere and Disk
Choosing between a sphere and a disk depends on the application's spatial requirements and performance criteria. Spheres offer uniform symmetry and optimal volume-to-surface area ratio, making them ideal for minimizing material use while maximizing enclosed space. Disks provide simplicity and ease of manufacturing with flat surfaces, suited for applications requiring planar geometry and stability.
Sphere Infographic
 libterm.com
libterm.com