A coset is a fundamental concept in group theory, representing a subset formed by multiplying all elements of a subgroup by a fixed element from the larger group. Understanding cosets is essential for exploring group structures, Lagrange's theorem, and the partitioning of groups into disjoint subsets of equal size. Discover how cosets reveal the intricate symmetry within algebraic systems by reading the rest of this article.
Table of Comparison
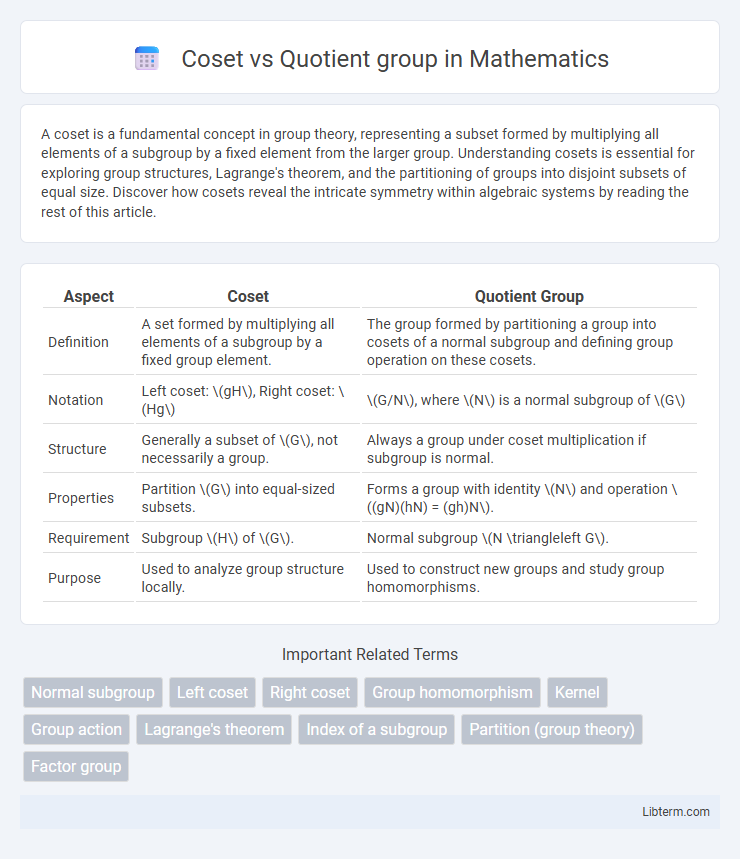
| Aspect | Coset | Quotient Group |
|---|---|---|
| Definition | A set formed by multiplying all elements of a subgroup by a fixed group element. | The group formed by partitioning a group into cosets of a normal subgroup and defining group operation on these cosets. |
| Notation | Left coset: \(gH\), Right coset: \(Hg\) | \(G/N\), where \(N\) is a normal subgroup of \(G\) |
| Structure | Generally a subset of \(G\), not necessarily a group. | Always a group under coset multiplication if subgroup is normal. |
| Properties | Partition \(G\) into equal-sized subsets. | Forms a group with identity \(N\) and operation \((gN)(hN) = (gh)N\). |
| Requirement | Subgroup \(H\) of \(G\). | Normal subgroup \(N \triangleleft G\). |
| Purpose | Used to analyze group structure locally. | Used to construct new groups and study group homomorphisms. |
Introduction to Cosets and Quotient Groups
Cosets are subsets formed by multiplying all elements of a subgroup H by a fixed element g from a group G, resulting in either left cosets gH or right cosets Hg, which partition the group G into disjoint equivalence classes. Quotient groups, denoted as G/H, arise when the subgroup H is normal in G, allowing the set of cosets to inherit a group structure under the operation defined by (gH)(kH) = (gk)H. Understanding cosets and quotient groups is fundamental in group theory, as they facilitate the study of group homomorphisms, factor groups, and the classification of group structures.
Defining Cosets in Group Theory
Cosets in group theory are subsets formed by multiplying a fixed element from the group with all elements of a subgroup, either from the left or the right, resulting in left cosets or right cosets respectively. If \( H \) is a subgroup of \( G \) and \( g \in G \), the left coset is defined as \( gH = \{ gh : h \in H \} \), while the right coset is \( Hg = \{ hg : h \in H \} \). These cosets partition the group \( G \) into disjoint equivalence classes, essential for understanding quotient groups where the set of all cosets \( G/H \) inherits a group structure when \( H \) is normal.
Understanding Quotient Groups
Quotient groups arise by partitioning a group \(G\) into cosets of a normal subgroup \(N\), forming the set \(G/N\) where each element is a coset \(gN\). The operation on \(G/N\) is well-defined due to the normality of \(N\), enabling multiplication of cosets \(gN \cdot hN = (gh)N\). Understanding quotient groups involves recognizing how the subgroup structure influences the group structure of \(G/N\), effectively capturing the "factorization" of \(G\) by \(N\).
Key Differences Between Cosets and Quotient Groups
Cosets are subsets formed by multiplying a fixed element with every element of a subgroup, while quotient groups arise by partitioning a group into these cosets, endowing the set of cosets with a group structure. A key difference is that cosets are mere subsets without inherent group operations, whereas quotient groups possess defined group operations making them groups themselves. The quotient group G/H exists only when H is a normal subgroup, a condition not required for defining cosets.
The Role of Normal Subgroups
Normal subgroups play a crucial role in the formation of quotient groups, as they ensure that the set of cosets forms a group under the operation induced by the original group. Only when a subgroup N is normal in G do the left cosets gN coincide with the right cosets Ng, allowing the well-defined group structure of the quotient group G/N. This property is essential for analyzing group homomorphisms and understanding the internal structure of groups through factorization.
Properties of Cosets in Groups
Cosets in groups partition the group into disjoint subsets of equal size, each formed by multiplying a subgroup by a fixed group element. Every left coset of a subgroup has the same cardinality as the subgroup itself, reflecting the subgroup's index in the group. The collection of all cosets forms a quotient group when the subgroup is normal, ensuring well-defined group operations on the set of cosets.
Constructing a Quotient Group: Step-by-Step
Constructing a quotient group begins by identifying a normal subgroup \( N \) within a group \( G \), ensuring \( N \) is invariant under conjugation by elements of \( G \). Next, form the set of left cosets \( gN = \{gn : n \in N\} \) for each \( g \in G \), creating a partition of \( G \) into equivalence classes. Defining the group operation on these cosets as \( (gN)(hN) = (gh)N \) establishes the quotient group \( G/N \), preserving group structure through well-defined multiplication on cosets.
Examples Illustrating Cosets and Quotient Groups
Consider the group \( \mathbb{Z} \) of integers under addition with the subgroup \( 3\mathbb{Z} = \{ \ldots, -6, -3, 0, 3, 6, \ldots \} \). The left cosets of \( 3\mathbb{Z} \) in \( \mathbb{Z} \) are sets like \( 1 + 3\mathbb{Z} = \{ \ldots, -5, -2, 1, 4, 7, \ldots \} \), illustrating how elements are partitioned by equivalence classes. Forming the quotient group \( \mathbb{Z} / 3\mathbb{Z} \) results in a group with three elements representing these cosets, showcasing the structure of the quotient group as the group of cosets under addition mod 3.
Applications of Cosets and Quotient Groups
Cosets facilitate the classification of elements in a group relative to a subgroup, enabling the analysis of group structure and symmetry in fields like crystallography and coding theory. Quotient groups simplify complex groups by partitioning them into cosets, essential in homomorphism studies and simplifying algebraic structures in topology and quantum mechanics. Both cosets and quotient groups underpin modular arithmetic applications and facilitate the understanding of normal subgroups critical for group factorization in theoretical physics and cryptography.
Summary and Further Reading on Group Theory
Cosets partition a group into equal-sized subsets formed by multiplying a fixed element with all elements of a subgroup, serving as a foundational concept for constructing quotient groups. Quotient groups, or factor groups, arise from these cosets when the subgroup is normal, enabling the group operation to be well-defined on the set of cosets and simplifying group structure analysis. For deeper exploration, refer to standard texts such as "Abstract Algebra" by Dummit and Foote and "Algebra" by Michael Artin, which provide comprehensive insights into cosets, normal subgroups, and quotient group formation within group theory.
Coset Infographic
 libterm.com
libterm.com