Circular design focuses on creating products that minimize waste through reuse, recycling, and sustainable materials, promoting a closed-loop system that benefits the environment. By adopting circular principles, businesses can reduce their ecological footprint while enhancing resource efficiency and economic resilience. Discover how circular strategies can transform your approach to sustainability in the rest of this article.
Table of Comparison
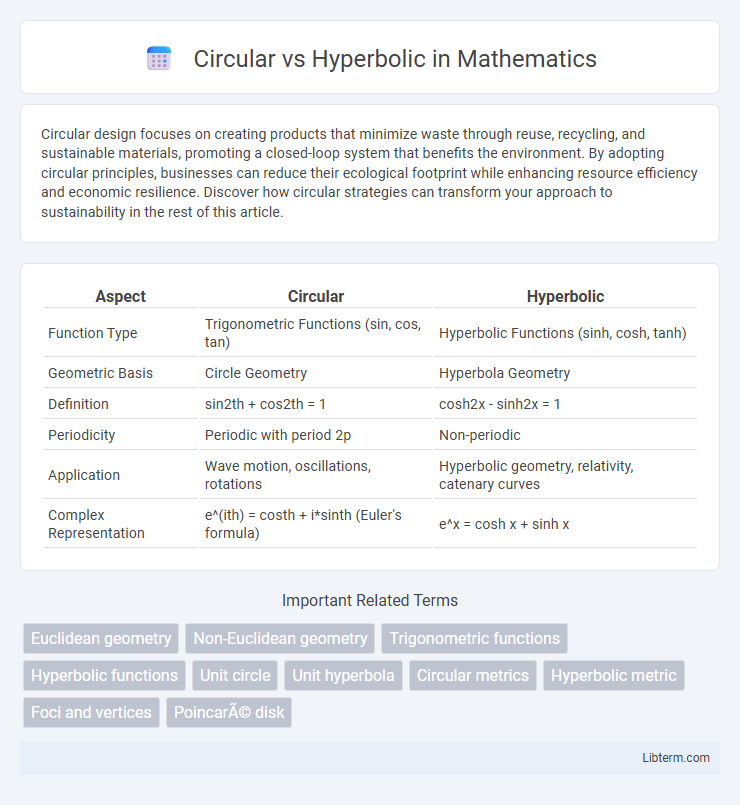
| Aspect | Circular | Hyperbolic |
|---|---|---|
| Function Type | Trigonometric Functions (sin, cos, tan) | Hyperbolic Functions (sinh, cosh, tanh) |
| Geometric Basis | Circle Geometry | Hyperbola Geometry |
| Definition | sin2th + cos2th = 1 | cosh2x - sinh2x = 1 |
| Periodicity | Periodic with period 2p | Non-periodic |
| Application | Wave motion, oscillations, rotations | Hyperbolic geometry, relativity, catenary curves |
| Complex Representation | e^(ith) = costh + i*sinth (Euler's formula) | e^x = cosh x + sinh x |
Introduction to Circular and Hyperbolic Concepts
Circular and hyperbolic concepts originate from distinct geometric frameworks, where circular geometry deals with the properties of points on a circle and angles subtended by arcs, foundational in trigonometry and Euclidean space analysis. Hyperbolic geometry explores the behavior of figures in a space with constant negative curvature, challenging Euclidean postulates and offering insights into non-Euclidean spaces and general relativity. These fundamental differences in curvature and distance metrics define unique applications and theoretical implications in mathematics and physics.
Defining Circular Functions
Circular functions, including sine, cosine, and tangent, are defined based on the unit circle, where angles correspond to points on the circle's circumference. These functions describe the relationship between an angle and the coordinates of a point on the circle, with sine and cosine representing the y and x coordinates, respectively. Circular functions are fundamental in trigonometry and are used to model periodic phenomena such as sound waves, light, and oscillations.
Understanding Hyperbolic Functions
Hyperbolic functions, including sinh, cosh, and tanh, play a crucial role in various fields such as engineering, physics, and complex analysis by modeling growth and decay processes with exponential components. Unlike circular functions based on the unit circle, hyperbolic functions are derived from the hyperbola x2 - y2 = 1 and relate closely to exponential functions through identities like cosh2x - sinh2x = 1. Mastery of hyperbolic functions enhances the ability to solve differential equations, analyze catenary curves, and apply transformations in hyperbolic geometry, underpinning their importance in advanced mathematical applications.
Historical Background and Development
Circular functions originated in ancient Greek mathematics, with Hipparchus and Ptolemy using chords of circles to study angles and solve astronomical problems. Hyperbolic functions emerged in the 18th century through the work of mathematicians like Johann Heinrich Lambert and Vincenzo Riccati, who explored analogies between circular trigonometric functions and hyperbolas. The development of hyperbolic functions was closely linked to calculus and the study of exponential growth, leading to applications in areas such as physics and engineering.
Mathematical Differences: Circular vs Hyperbolic
Circular functions, such as sine and cosine, are based on the unit circle and describe periodic phenomena with values oscillating between -1 and 1. Hyperbolic functions, including sinh and cosh, derive from the unit hyperbola and exhibit exponential growth and decay without periodicity. The fundamental identities differ: circular functions satisfy \( \sin^2 x + \cos^2 x = 1 \), whereas hyperbolic functions follow \( \cosh^2 x - \sinh^2 x = 1 \).
Geometric Interpretations
Circular geometry interprets angles and distances on a plane using circles, where the sum of triangle angles always equals 180 degrees. Hyperbolic geometry, represented on a saddle-shaped surface, features triangles with angle sums less than 180 degrees and lines diverging away from each other. These distinct geometric interpretations reflect the fundamental differences between Euclidean and non-Euclidean spaces in curvature and parallel line behavior.
Applications in Science and Engineering
Circular functions such as sine and cosine play a critical role in engineering fields like signal processing, control systems, and mechanical vibrations due to their periodic nature and ability to model oscillatory behavior. Hyperbolic functions, including sinh and cosh, are fundamental in areas like heat transfer, special relativity, and structural engineering for modeling growth, decay, and certain nonlinear phenomena. Both function types facilitate solving differential equations, but circular functions excel in periodic system analysis while hyperbolic functions better describe exponential-like growth and decay processes.
Key Formulas and Identities
Circular functions include sine, cosine, and tangent, with key identities such as \( \sin^2 x + \cos^2 x = 1 \) and angle addition formulas like \( \sin(a \pm b) = \sin a \cos b \pm \cos a \sin b \). Hyperbolic functions, including sinh, cosh, and tanh, satisfy identities like \( \cosh^2 x - \sinh^2 x = 1 \) and share similar addition formulas \( \sinh(a \pm b) = \sinh a \cosh b \pm \cosh a \sinh b \). Both sets of functions play crucial roles in calculus, complex analysis, and solving differential equations, with circular functions linked to unit circles and hyperbolic functions associated with hyperbolas.
Real-World Examples and Case Studies
Circular functions like sine and cosine model periodic phenomena such as sound waves, tides, and seasonal temperature variations. Hyperbolic functions, including sinh and cosh, describe real-world scenarios like the shape of a hanging cable (catenary curve), the distribution of electric fields, and special relativity's spacetime intervals. Case studies in engineering highlight circular functions in oscillatory systems, while hyperbolic functions play a crucial role in solving differential equations for heat transfer and fluid dynamics.
Summary: Choosing Between Circular and Hyperbolic
Circular and hyperbolic functions serve different mathematical and practical purposes, each optimized for specific applications such as engineering or physics. Circular functions model periodic phenomena and rotations, while hyperbolic functions relate to exponential growth, decay, and hyperbolic geometry. Selecting between circular and hyperbolic depends on the problem context--use circular for oscillations and waves, and hyperbolic for processes involving rapid changes or hyperbolic shapes.
Circular Infographic
 libterm.com
libterm.com