A Lebesgue measurable set is a fundamental concept in measure theory, characterized by its compatibility with the Lebesgue measure, enabling the assignment of a consistent "size" or measure to a wide class of subsets in real numbers. This concept extends beyond simple geometric shapes, allowing the measurement of more complex and irregular sets, essential for advanced analysis and integration. Explore this article to deepen your understanding of Lebesgue measurable sets and their crucial role in modern mathematical analysis.
Table of Comparison
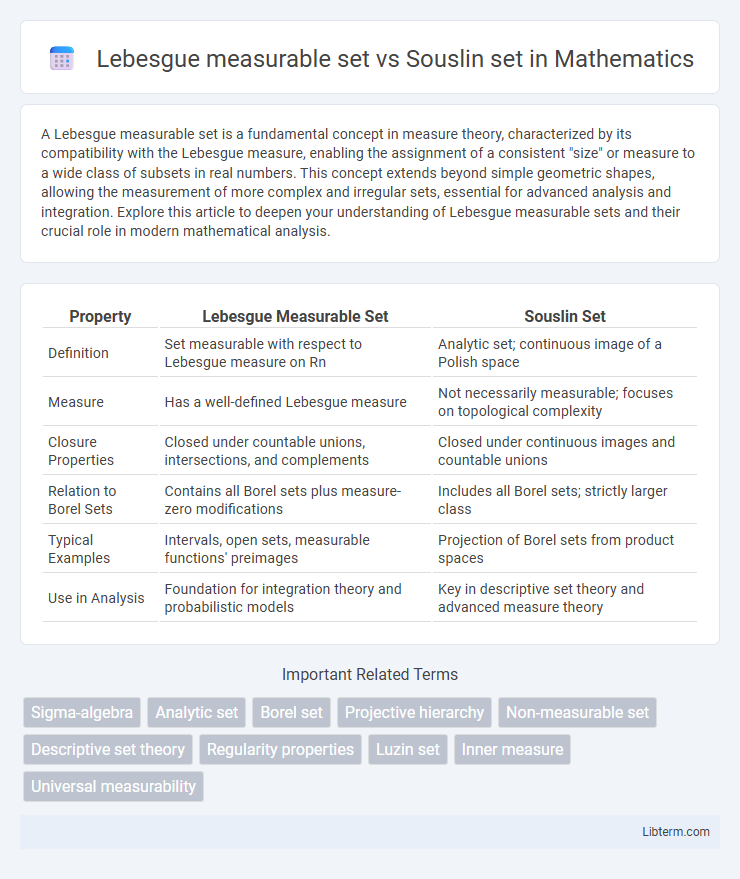
| Property | Lebesgue Measurable Set | Souslin Set |
|---|---|---|
| Definition | Set measurable with respect to Lebesgue measure on Rn | Analytic set; continuous image of a Polish space |
| Measure | Has a well-defined Lebesgue measure | Not necessarily measurable; focuses on topological complexity |
| Closure Properties | Closed under countable unions, intersections, and complements | Closed under continuous images and countable unions |
| Relation to Borel Sets | Contains all Borel sets plus measure-zero modifications | Includes all Borel sets; strictly larger class |
| Typical Examples | Intervals, open sets, measurable functions' preimages | Projection of Borel sets from product spaces |
| Use in Analysis | Foundation for integration theory and probabilistic models | Key in descriptive set theory and advanced measure theory |
Introduction to Measurable and Souslin Sets
Lebesgue measurable sets are fundamental objects in measure theory characterized by their compatibility with the Lebesgue measure, allowing for rigorous integration and manipulation within real analysis. Souslin sets, also known as analytic sets, arise from projections of Borel sets in Polish spaces and hold significance in descriptive set theory, providing a broader class that may not always be measurable. Understanding the distinction and relationship between Lebesgue measurable sets and Souslin sets is crucial for advanced studies in real analysis and set-theoretic topology.
Defining Lebesgue Measurable Sets
Lebesgue measurable sets are defined within the framework of measure theory as subsets of real numbers that can be approximated from the outside and inside by open or closed sets with arbitrarily small differences in measure. A set \(E \subseteq \mathbb{R}\) is Lebesgue measurable if for every \(\epsilon > 0\), there exists an open set \(O\) containing \(E\) such that the Lebesgue outer measure \(m^*(O \setminus E) < \epsilon\). In contrast, Souslin sets, also known as analytic sets, arise from descriptive set theory and are defined as continuous images of Borel sets but are not necessarily measurable with respect to Lebesgue measure.
Understanding Souslin Sets (Analytic Sets)
Souslin sets, also known as analytic sets, are projections of Borel sets in a product space and play a crucial role in descriptive set theory and measure theory, bridging the gap between Borel and Lebesgue measurable sets. While all Borel sets are Lebesgue measurable, Souslin sets extend this class and include some non-Borel sets that remain Lebesgue measurable under complete measure extensions. Understanding Souslin sets involves grasping their definability through continuous images of Polish spaces, which highlights their significance in the hierarchy of measurable sets beyond classical Borel classifications.
Properties of Lebesgue Measurable Sets
Lebesgue measurable sets are characterized by their closure under countable unions, intersections, and complementation, ensuring they form a complete s-algebra on the real line. These sets possess the property of measure completeness, meaning every subset of a null Lebesgue measurable set is also measurable with measure zero. In contrast, Souslin sets, generated from continuous images of Borel sets, may not always be Lebesgue measurable but have strong descriptive set-theoretic structure.
Key Characteristics of Souslin Sets
Souslin sets, also known as analytic sets, are projections of Borel sets in a Polish space and possess closure properties under continuous mappings and countable unions, making them more general than Lebesgue measurable sets. Unlike Lebesgue measurable sets, which are defined via measure theory, Souslin sets are characterized by their descriptive set-theoretic construction, often used to analyze complex sets beyond Borel measurability. They play a crucial role in descriptive set theory due to their well-behaved structure, including stability under Suslin operation and possessing the property of being universally measurable.
Relationship between Measurable and Souslin Sets
Lebesgue measurable sets form a s-algebra that includes all Borel sets and is closed under measure-theoretic operations, while Souslin sets, defined via continuous images of Borel sets, strictly extend the class of Borel sets but may not be Lebesgue measurable. Every Lebesgue measurable set can be approximated by Borel sets to arbitrary precision in measure, but not all Souslin sets are guaranteed to be measurable under the Lebesgue measure. The interplay between these classes is central in descriptive set theory, highlighting that Souslin sets are analytic and universally measurable in Polish spaces, thus encompassing Lebesgue measurable sets within a broader framework.
Examples of Lebesgue Measurable vs. Souslin Sets
Examples of Lebesgue measurable sets include all Borel sets, such as open intervals, closed intervals, and countable unions or intersections of these sets, as well as sets differing from Borel sets by a measure zero set. Souslin sets, also known as analytic sets, include all Borel sets but further extend to continuous images of Borel sets, such as the projection of a Borel subset of a plane onto the real line, which may not be Borel measurable yet remain Lebesgue measurable. An important distinction is that while every Borel set is both Lebesgue measurable and Souslin, certain Souslin sets serve as examples of Lebesgue measurable sets that are not Borel, illustrating the strict inclusion of the Borel s-algebra within the class of Souslin sets.
The Role of Polish Spaces in Set Theory
Polish spaces provide a crucial framework for analyzing Lebesgue measurable sets and Souslin sets by offering a complete separable metric structure that facilitates their topological and measure-theoretic properties. Lebesgue measurable sets often arise as measurable subsets within Polish spaces equipped with Borel sigma-algebras, while Souslin sets, also known as analytic sets, are continuous images of Borel sets from Polish spaces, highlighting their definability in descriptive set theory. The interplay between Polish spaces and these sets allows for deep insights into hierarchies of complexity and measurability in modern set theory.
Applications in Measure Theory and Descriptive Set Theory
Lebesgue measurable sets form the cornerstone of modern measure theory, providing a robust framework for integration, probability, and real analysis by ensuring well-defined measures under countable operations. Souslin sets, arising from descriptive set theory, extend classical Borel structures and facilitate fine-grained classification of analytic sets crucial for advanced measurable selection theorems and hierarchy analyses. The interplay between Lebesgue measurability and Souslin sets enables deeper insights into regularity properties, classification of pathological sets, and the development of refined measurable structures in both pure and applied mathematical contexts.
Summary: Comparing Lebesgue Measurable and Souslin Sets
Lebesgue measurable sets are defined through their compatibility with Lebesgue measure, allowing accurate measure assignment and integration on the real line. Souslin sets, also known as analytic sets, arise from continuous images of Borel sets and encompass a broader class that includes all Borel and many non-Borel sets but may lack direct measure assignability. While every Borel set is both Lebesgue measurable and Souslin, Souslin sets extend beyond measurable sets, highlighting differences in definability and measurability within descriptive set theory and measure theory.
Lebesgue measurable set Infographic
 libterm.com
libterm.com