Deformation refers to the alteration in the shape or size of a material under applied stress, which can be elastic or plastic depending on the material's properties. Understanding how materials deform is crucial for predicting structural integrity and performance in engineering applications. Discover how deformation impacts design and safety by reading the rest of this article.
Table of Comparison
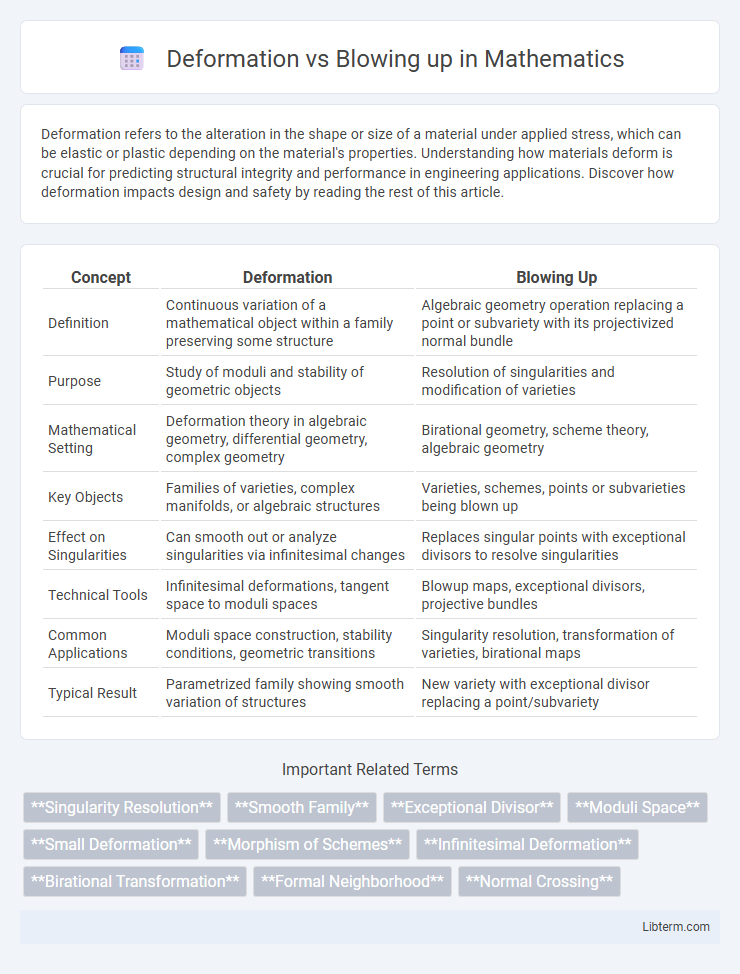
| Concept | Deformation | Blowing Up |
|---|---|---|
| Definition | Continuous variation of a mathematical object within a family preserving some structure | Algebraic geometry operation replacing a point or subvariety with its projectivized normal bundle |
| Purpose | Study of moduli and stability of geometric objects | Resolution of singularities and modification of varieties |
| Mathematical Setting | Deformation theory in algebraic geometry, differential geometry, complex geometry | Birational geometry, scheme theory, algebraic geometry |
| Key Objects | Families of varieties, complex manifolds, or algebraic structures | Varieties, schemes, points or subvarieties being blown up |
| Effect on Singularities | Can smooth out or analyze singularities via infinitesimal changes | Replaces singular points with exceptional divisors to resolve singularities |
| Technical Tools | Infinitesimal deformations, tangent space to moduli spaces | Blowup maps, exceptional divisors, projective bundles |
| Common Applications | Moduli space construction, stability conditions, geometric transitions | Singularity resolution, transformation of varieties, birational maps |
| Typical Result | Parametrized family showing smooth variation of structures | New variety with exceptional divisor replacing a point/subvariety |
Introduction to Deformation and Blowing Up
Deformation refers to the process of smoothly transforming a geometric object or algebraic variety by varying its defining parameters, revealing local and global structural changes within families of shapes. Blowing up is a specific type of transformation in algebraic geometry that replaces a point or subvariety with an entire divisor, often a projective space, to resolve singularities or analyze intricate geometric properties. Understanding these concepts is critical for studying complex spaces, as deformations explore continuous variations while blow-ups provide controlled modifications that uncover hidden structure.
Definitions: What is Deformation?
Deformation refers to the process in algebraic geometry where a geometric object is smoothly transformed or varied within a family of objects, preserving certain properties while altering shape or structure infinitesimally. It studies small perturbations of varieties or schemes, providing insight into their local behavior and moduli spaces. Unlike blowing up, deformation focuses on continuous changes rather than discrete modifications at points or subvarieties.
Definitions: What is Blowing Up?
Blowing up is a geometric transformation in algebraic geometry that replaces a point or subvariety in a space with an entire projective space, effectively resolving singularities or creating a new variety with better properties. This process is a specific type of deformation where the original space is modified by introducing exceptional divisors that reflect the local structure near the blown-up point. Unlike general deformations that continuously vary the shape of a variety, blowing up fundamentally alters its local topology and algebraic structure to simplify singular points.
Historical Context and Mathematical Motivation
Deformation theory, rooted in the pioneering works of Kodaira and Spencer in the mid-20th century, investigates how geometric structures smoothly change under small perturbations, providing insights into moduli spaces and complex manifold classifications. Blowing up, with origins tracing back to Zariski and Hironaka's resolution of singularities in algebraic geometry, is motivated by the need to replace singular points with simpler geometric configurations that enable rigorous analysis and manipulation. Both techniques serve as foundational tools in modern algebraic geometry, addressing singularities and continuity issues through complementary approaches focused on local and global structural modifications.
Key Differences Between Deformation and Blowing Up
Deformation alters a geometric object through continuous transformations, preserving its topological properties while changing its shape or structure locally or globally. Blowing up replaces a point or subvariety of an algebraic variety with a higher-dimensional space, such as a projective space, to resolve singularities or study local behavior. Key differences include deformation's focus on smooth changes without introducing new points, whereas blowing up creates new geometric spaces to replace singularities.
Applications in Algebraic Geometry
Deformation theory in algebraic geometry studies how algebraic varieties change under small perturbations, providing insight into moduli spaces and local properties of schemes. Blowing up is a birational transformation used to resolve singularities by replacing points or subvarieties with exceptional divisors, thus modifying the variety to a smoother model. Combining deformation and blowing up techniques enables precise control over singular behavior, facilitating classifications of algebraic surfaces and complex moduli problems.
Examples Illustrating Deformation
In algebraic geometry, deformation refers to the process of continuously transforming a variety into another by varying parameters, exemplified by smoothing a nodal curve into a nonsingular one. An example includes deforming a singular surface defined by \(xy=0\) into a smooth surface \(xy=t\) for \(t \neq 0\), demonstrating how singularities can be resolved through parameter changes. Unlike blowing up, which replaces a point with an entire projective space to resolve singularities, deformations adjust the shape or structure without introducing new geometric components.
Examples Illustrating Blowing Up
Blowing up in algebraic geometry replaces a point or subvariety with all limiting tangent directions, transforming singularities into simpler structures. For example, blowing up the origin in the plane replaces it with a projective line representing directions through that point, resolving curve singularities like nodes or cusps. In contrast, deformation theory studies smooth families of varieties changing parameters continuously without such drastic topological modifications.
Interplay Between Deformation and Blowing Up
The interplay between deformation and blowing up reveals profound impacts on singularity resolution and geometric structure transformations in algebraic geometry. Deformation modifies a variety's local geometry through smooth parameter changes, while blowing up replaces singular points with higher-dimensional exceptional divisors, refining the variety's topology. Understanding how deformations influence the behavior and necessity of blowups enhances strategies for resolving complex singularities and constructing minimal models.
Conclusion: Comparing Deformation vs Blowing Up
Deformation and blowing up serve distinct roles in algebraic geometry by altering a variety's structure to reveal different geometric properties. Deformation examines continuous transformations that preserve underlying characteristics, while blowing up replaces a point with a projective space to resolve singularities. Comparing both reveals deformation as a tool for studying moduli and families, whereas blowing up is essential for desingularization and local modification.
Deformation Infographic
 libterm.com
libterm.com