A projective variety is a subset of projective space defined as the zeros of a set of homogeneous polynomials, forming a key object of study in algebraic geometry. These varieties exhibit rich geometric and algebraic properties, including dimension, degree, and singularities, which help characterize complex shapes in a projective setting. Explore the rest of the article to deepen your understanding of projective varieties and their significant applications.
Table of Comparison
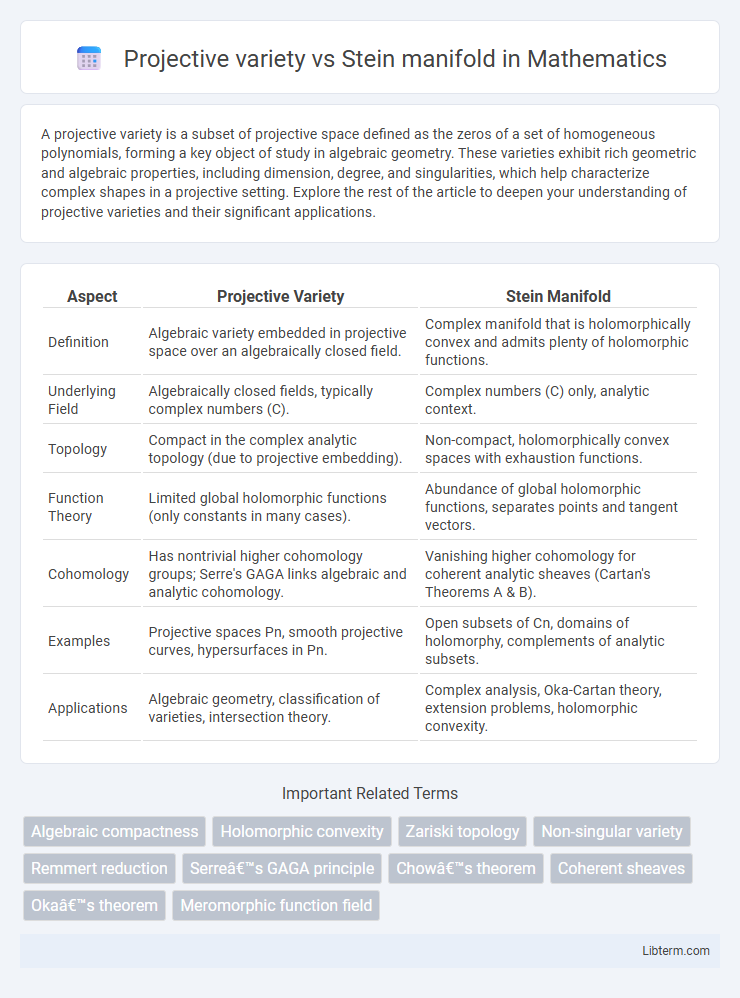
| Aspect | Projective Variety | Stein Manifold |
|---|---|---|
| Definition | Algebraic variety embedded in projective space over an algebraically closed field. | Complex manifold that is holomorphically convex and admits plenty of holomorphic functions. |
| Underlying Field | Algebraically closed fields, typically complex numbers (C). | Complex numbers (C) only, analytic context. |
| Topology | Compact in the complex analytic topology (due to projective embedding). | Non-compact, holomorphically convex spaces with exhaustion functions. |
| Function Theory | Limited global holomorphic functions (only constants in many cases). | Abundance of global holomorphic functions, separates points and tangent vectors. |
| Cohomology | Has nontrivial higher cohomology groups; Serre's GAGA links algebraic and analytic cohomology. | Vanishing higher cohomology for coherent analytic sheaves (Cartan's Theorems A & B). |
| Examples | Projective spaces Pn, smooth projective curves, hypersurfaces in Pn. | Open subsets of Cn, domains of holomorphy, complements of analytic subsets. |
| Applications | Algebraic geometry, classification of varieties, intersection theory. | Complex analysis, Oka-Cartan theory, extension problems, holomorphic convexity. |
Introduction to Projective Varieties and Stein Manifolds
Projective varieties are fundamental objects in algebraic geometry defined as the zero sets of homogeneous polynomials in projective space, exhibiting properties such as compactness and algebraic structure. Stein manifolds, central in complex analysis, are complex manifolds characterized by holomorphic convexity and the existence of plentiful holomorphic functions, often serving as the analytic counterpart to affine varieties. Understanding the distinction between projective varieties and Stein manifolds involves contrasting their inherently algebraic nature and compactness against the topologically flexible, holomorphically rich structure of Stein manifolds.
Algebraic Foundations of Projective Varieties
Projective varieties are algebraic sets defined as the zero loci of homogeneous polynomials in projective space, grounded in commutative algebra and algebraic geometry through ideals and coordinate rings. Stein manifolds, on the other hand, arise in complex analytic geometry, characterized by holomorphic convexity and the existence of sufficiently many global holomorphic functions, lacking direct algebraic structure. The algebraic foundations of projective varieties involve graded rings and homogeneous coordinate rings, enabling the use of tools like Hilbert's Nullstellensatz and cohomology theories, which are absent in the analytic framework defining Stein manifolds.
Complex Analytic Structure of Stein Manifolds
Projective varieties are algebraic sets defined by homogeneous polynomial equations in complex projective space, characterized by their rigid algebraic structure and compactness, whereas Stein manifolds are complex analytic spaces that generalize complex Euclidean domains with crucial properties such as holomorphic convexity, holomorphic separability, and the existence of ample holomorphic functions. The complex analytic structure of Stein manifolds allows for the application of powerful tools like Cartan's Theorems A and B, ensuring the solvability of the Cousin problems and enabling holomorphic function theory to fully develop. Unlike projective varieties, Stein manifolds are non-compact and provide a flexible analytic framework important for embedding theorems and complex geometric analysis.
Topological Properties: Compactness and Connectivity
Projective varieties, defined as zero loci of homogeneous polynomials in complex projective space, are inherently compact due to the compactness of complex projective space itself, and their topological connectivity is often linked to irreducibility and singularities. Stein manifolds, as complex analytic analogs of affine varieties, are non-compact but holomorphically convex, exhibiting strong topological properties such as homotopy equivalence to CW complexes of dimension at most equal to their complex dimension, with connectivity influenced by the absence of compact complex subvarieties. The contrast between the compactness of projective varieties and the holomorphic convexity but non-compactness of Stein manifolds underpins fundamental topological distinctions relevant in complex geometry and several complex variables.
Morphisms and Maps: Holomorphic vs. Algebraic
Projective varieties admit morphisms defined by homogeneous polynomials, ensuring algebraic maps with rigid structures, while Stein manifolds feature holomorphic maps characterized by complex analytic functions preserving local complex structures. Morphisms between projective varieties are algebraic and respect the scheme-theoretic framework, whereas holomorphic maps on Stein manifolds allow greater flexibility, enabling embedding into complex Euclidean spaces by Cartan's Theorems A and B. The contrast between algebraic morphisms and holomorphic maps highlights the interplay between algebraic geometry and complex analysis in defining map structures on these spaces.
Cohomology and Function Theory Insights
Projective varieties exhibit rich cohomological structures characterized by Hodge theory and Serre duality, enabling algebraic methods to solve geometric problems, while Stein manifolds possess vanishing higher cohomology for coherent analytic sheaves, reflecting their function-theoretic flexibility and holomorphic convexity. The cohomology of projective varieties often encodes algebraic invariants linked to divisors and line bundles, contrasting with Stein manifolds whose function theory is governed by Cartan's theorems A and B, guaranteeing ample global holomorphic functions. These distinct cohomological and analytical properties reveal deep contrasts: projective varieties serve as compact algebraic models with constrained analytic flexibility, whereas Stein manifolds provide non-compact complex analytic spaces enabling extensive holomorphic function extension and approximation.
Embedding Theorems and Realizations
Projective varieties embed naturally into complex projective space via well-known embedding theorems such as the Kodaira embedding theorem, which guarantees that ample line bundles induce projective embeddings. Stein manifolds, characterized by their holomorphic convexity and the existence of plenty of global holomorphic functions, are realized as closed complex submanifolds of complex Euclidean spaces by the Remmert and Bishop embedding theorems. While projective varieties are algebraic and compact, Stein manifolds serve as the analytic counterpart, allowing holomorphic embeddings into affine spaces but lack the compactness and algebraic structure inherent in projective varieties.
Examples Illustrating Projective Varieties and Stein Manifolds
Projective varieties, such as elliptic curves defined by homogeneous polynomials in complex projective space \(\mathbb{CP}^n\), exemplify compact complex algebraic varieties with rich geometric structures. Stein manifolds include complex Euclidean spaces \(\mathbb{C}^n\) and open Riemann surfaces, characterized by holomorphic convexity and the existence of plenty of global holomorphic functions. These examples highlight the stark contrast: projective varieties are compact and algebraic, whereas Stein manifolds are non-compact, holomorphically convex, and analytically flexible.
Fundamental Differences and Intersections
Projective varieties are complex algebraic varieties embedded in projective space characterized by their compactness and algebraic structure defined by homogeneous polynomial equations. Stein manifolds are complex analytic spaces that are holomorphically convex, holomorphically separable, and exhibit the property of possessing plenty of global holomorphic functions, typically non-compact and affine-like. The fundamental difference lies in projective varieties being compact with rich algebraic geometry, while Stein manifolds serve as the analytic counterpart of affine varieties, allowing strong function theory, yet intersections occur when a projective variety minus a suitable divisor can form a Stein manifold.
Applications and Open Problems in Modern Geometry
Projective varieties, defined as zeros of homogeneous polynomials in projective space, are fundamental objects in algebraic geometry with applications in enumerative geometry, moduli theory, and string theory. Stein manifolds, characterized by their holomorphic convexity and rich function theory, play a crucial role in complex analysis, deformation theory, and complex differential geometry. Open problems focus on the characterization of embeddings between these structures, classification of their morphisms, and the exploration of their roles in mirror symmetry and complex dynamics within modern geometric frameworks.
Projective variety Infographic
 libterm.com
libterm.com