A subgroup is a subset of a group that itself forms a group under the same operation, satisfying closure, identity, and invertibility properties. Understanding subgroups is essential for analyzing the internal structure of mathematical groups and their symmetries. Explore the rest of this article to deepen your understanding of subgroups and their applications.
Table of Comparison
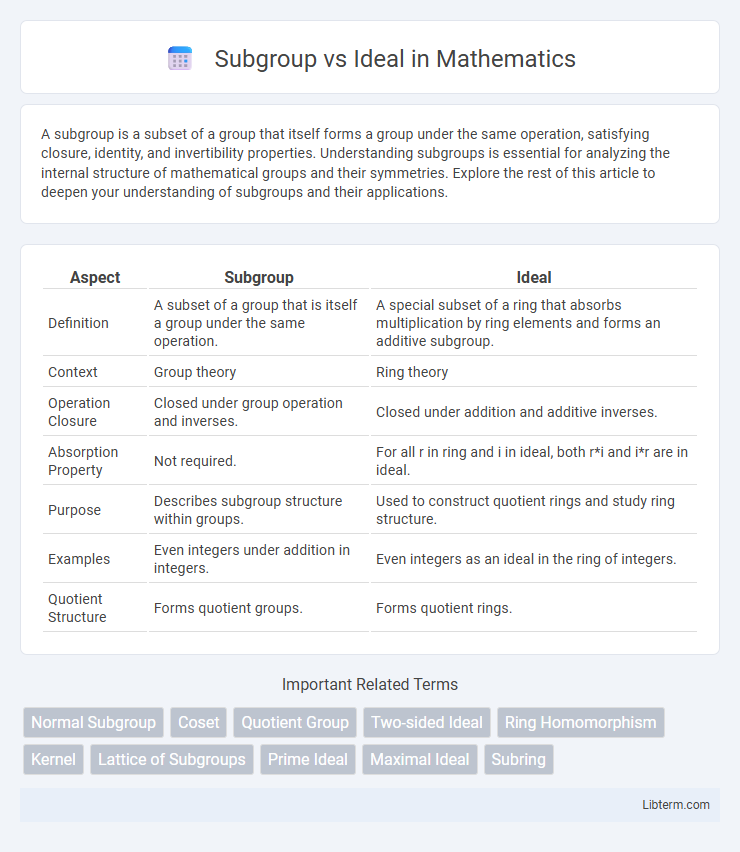
| Aspect | Subgroup | Ideal |
|---|---|---|
| Definition | A subset of a group that is itself a group under the same operation. | A special subset of a ring that absorbs multiplication by ring elements and forms an additive subgroup. |
| Context | Group theory | Ring theory |
| Operation Closure | Closed under group operation and inverses. | Closed under addition and additive inverses. |
| Absorption Property | Not required. | For all r in ring and i in ideal, both r*i and i*r are in ideal. |
| Purpose | Describes subgroup structure within groups. | Used to construct quotient rings and study ring structure. |
| Examples | Even integers under addition in integers. | Even integers as an ideal in the ring of integers. |
| Quotient Structure | Forms quotient groups. | Forms quotient rings. |
Definition of Subgroup and Ideal
A subgroup is a subset of a group that itself satisfies the group axioms under the same operation, ensuring closure, identity, and inverses within the subset. An ideal is a special subset of a ring that absorbs multiplication by any element in the ring and forms an additive subgroup, enabling the construction of quotient rings. While subgroups relate primarily to group theory structure, ideals are fundamental in ring theory and abstract algebra, serving as kernels of ring homomorphisms.
Key Differences Between Subgroups and Ideals
Subgroups are subsets of a group that themselves form a group under the same operation, emphasizing closure, identity, and invertibility within the parent group. Ideals, specifically in ring theory, are special subsets that absorb multiplication by elements from the ring and facilitate the construction of quotient rings. The key differences lie in their algebraic context--subgroups pertain to group theory focusing on group properties, while ideals relate to ring theory with absorption and ideal-related operations.
Algebraic Structures Involving Subgroups
In algebraic structures, a subgroup is a subset of a group that itself forms a group under the same operation, preserving closure, identity, and inverses. An ideal, primarily defined within ring theory, is a special subset that absorbs multiplication by ring elements and allows the construction of quotient rings. While subgroups focus on group properties, ideals play a crucial role in ring homomorphisms and factor rings, highlighting their fundamental differences in algebraic structures involving subgroups.
Role of Ideals in Ring Theory
Ideals in ring theory serve as crucial substructures that enable the construction of quotient rings, thereby facilitating the study of ring homomorphisms and divisibility properties. Unlike subgroups that focus solely on additive closure, ideals require absorption under ring multiplication, ensuring compatibility with the ring's multiplicative structure. This absorption property of ideals plays a central role in characterizing kernels of ring homomorphisms and in defining prime and maximal ideals essential for ring classification and factorization.
Criteria for Identifying Subgroups
Subgroups are identified by satisfying closure under the group operation and the presence of inverses within the subset, while ideals require absorption under multiplication by elements of the larger ring. The criteria for subgroups focus on verifying the subset is non-empty, closed under group operations, and includes inverses, ensuring it forms a group on its own. Ideals extend these conditions with additional constraints that integrate the subset within ring multiplication, distinguishing ideals from subgroups in algebraic structures.
Properties Unique to Ideals
Ideals in ring theory exhibit properties that distinguish them from subgroups, notably their absorption property where multiplication by any element of the ring remains within the ideal. Unlike arbitrary subgroups of rings that preserve addition and inverses, ideals ensure closure under both addition and ring multiplication, enabling the formation of quotient rings. This absorptive characteristic is essential for defining homomorphisms and factor rings, highlighting the structural significance of ideals beyond mere subgroup criteria.
Examples of Subgroups in Group Theory
In group theory, a subgroup is a subset of a group that itself forms a group under the same operation, such as the subgroup of integers under addition within the real numbers. In contrast, an ideal is a special subset in ring theory that absorbs multiplication by ring elements, seen clearly in examples like the set of even integers forming an ideal within the integers. Examples of subgroups include the cyclic subgroup generated by an element in a group, the trivial subgroup containing only the identity element, and normal subgroups, which are invariant under conjugation and play a crucial role in defining quotient groups.
Examples of Ideals in Ring Theory
In ring theory, an ideal is a special subset of a ring that absorbs multiplication by any element of the ring and forms a subgroup under addition, such as the set of even integers in the ring of all integers. An example of an ideal is the principal ideal generated by an element a in a ring R, denoted (a), consisting of all multiples of a, like 3Z in the ring of integers Z. Unlike general subgroups, ideals ensure the product of any ring element with an ideal element remains within the ideal, a key property used to construct quotient rings.
Applications of Subgroups and Ideals
Subgroups play a crucial role in group theory by enabling the classification of group structures and simplifying complex problems through their use in symmetry analysis and automorphism groups. Ideals are fundamental in ring theory as they facilitate the construction of quotient rings, which are essential for solving polynomial equations and analyzing algebraic structures in module theory. Both subgroups and ideals serve as building blocks in abstract algebra, with subgroups applied primarily in group homomorphisms and normality conditions, and ideals used extensively in factorization, ring homomorphisms, and algebraic geometry.
Subgroup vs Ideal: Summary Table
A subgroup is a subset of a group that itself satisfies the group axioms under the same operation, while an ideal is a special subset of a ring closed under addition and absorbing multiplication by any element of the ring. The summary table contrasts these structures by highlighting that subgroups require closure under inverses and associativity within groups, whereas ideals must absorb multiplication from ring elements and facilitate quotient ring formation. Key differences include the algebraic structures they belong to and the specific closure properties each must satisfy.
Subgroup Infographic
 libterm.com
libterm.com