Turing completeness defines a system's ability to perform any computation given enough resources, making it a fundamental concept in computer science and programming languages. Understanding this concept helps you recognize the limits and capabilities of different computational models. Explore the rest of the article to dive deeper into how Turing completeness impacts modern computing.
Table of Comparison
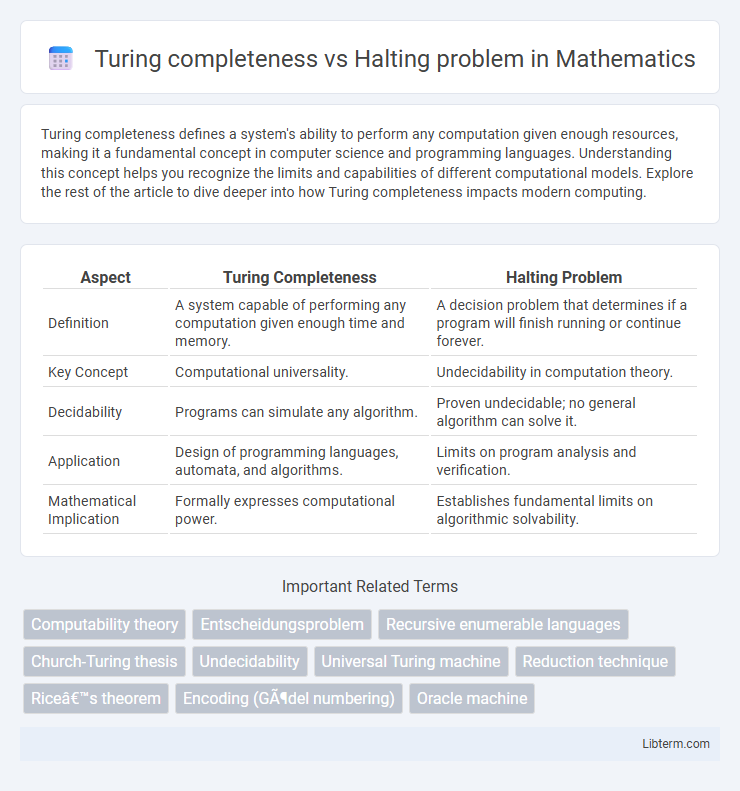
| Aspect | Turing Completeness | Halting Problem |
|---|---|---|
| Definition | A system capable of performing any computation given enough time and memory. | A decision problem that determines if a program will finish running or continue forever. |
| Key Concept | Computational universality. | Undecidability in computation theory. |
| Decidability | Programs can simulate any algorithm. | Proven undecidable; no general algorithm can solve it. |
| Application | Design of programming languages, automata, and algorithms. | Limits on program analysis and verification. |
| Mathematical Implication | Formally expresses computational power. | Establishes fundamental limits on algorithmic solvability. |
Introduction to Turing Completeness
Turing completeness defines a system capable of performing any computation that a Turing machine can execute, indicating the system's ability to simulate any algorithm. It serves as a benchmark for the computational power of programming languages and abstract machines. The halting problem demonstrates that no Turing-complete system can universally predict whether an arbitrary program will terminate or run indefinitely.
Understanding the Halting Problem
The Halting Problem is a fundamental concept in computability theory, demonstrating that it is impossible to create an algorithm that determines whether any given program will eventually stop or run indefinitely. This problem highlights the limits of Turing completeness, as even Turing machines, which can simulate any algorithm, cannot solve the Halting Problem for all possible inputs. Understanding the Halting Problem is crucial for grasping why certain computational questions remain undecidable and why some algorithms' behaviors cannot be predicted algorithmically.
Historical Context and Key Figures
Turing completeness, introduced by Alan Turing in 1936, characterizes computational systems capable of performing any algorithmic computation, forming the foundation of theoretical computer science. The Halting problem, also formulated by Turing, demonstrated the inherent undecidability of predicting whether a given program halts or runs indefinitely. Key figures such as Alonzo Church and Emil Post contributed to the development of computability theory, establishing the Church-Turing thesis linking effective computability and Turing machine models.
Formal Definitions and Concepts
Turing completeness is a property of computational systems that can simulate any Turing machine, meaning they can perform any computation given enough time and memory. The halting problem is a decision problem that determines whether a given Turing machine will halt on a specific input or run indefinitely, proven to be undecidable by Alan Turing. Formal definitions characterize Turing completeness through the ability to implement universal computational models, while the halting problem exemplifies inherent limits in algorithmic predictability within these systems.
Relationship Between Turing Completeness and the Halting Problem
The relationship between Turing completeness and the Halting problem lies in the computational power of Turing-complete systems, which can simulate any Turing machine, thereby inheriting the undecidability of the Halting problem. This means that no algorithm can universally determine whether an arbitrary program in a Turing-complete language will halt or run indefinitely. Hence, Turing completeness directly implies the presence of inherently unsolvable problems like the Halting problem within the computational framework.
Implications for Programming Languages
Turing completeness defines a programming language's ability to simulate any Turing machine, enabling the expression of any computable function. The Halting problem demonstrates that it is impossible to algorithmically determine whether arbitrary programs will terminate, highlighting fundamental limits on program analysis and verification. These implications mean that programming languages designed for general computation inherently cannot guarantee automatic detection of infinite loops or runtime termination, impacting compiler design, debugging tools, and formal verification methods.
Real-World Examples and Applications
Turing completeness defines a system's capability to simulate any Turing machine, enabling it to perform arbitrary computations, which is exemplified by modern programming languages like Python and JavaScript. The Halting problem, proven undecidable by Alan Turing, demonstrates the fundamental limit that no algorithm can predict with certainty whether any given program will stop or run indefinitely, affecting software verification and debugging tools. Real-world applications such as compilers, interpreters, and automated code analyzers rely on understanding Turing completeness to maximize computational power while navigating the implications of the Halting problem to avoid undecidable scenarios in practice.
Limitations and Challenges
Turing completeness signifies a system's ability to simulate any Turing machine, yet it inherently faces the Halting problem, which proves undecidable for all possible inputs and programs. This limitation restricts automated verification and leads to challenges in predicting program termination, impacting software reliability and correctness. The Halting problem emphasizes fundamental barriers in computability, driving ongoing research in decidability, program analysis, and computational theory.
Philosophical and Theoretical Considerations
Turing completeness defines systems capable of performing any computation given sufficient time and memory, highlighting the theoretical limits of algorithmic processes. The Halting problem exposes inherent undecidability by proving no algorithm can universally determine whether arbitrary programs halt, underscoring fundamental constraints in computation theory. These concepts challenge the philosophical understanding of computability, algorithmic predictability, and the limits of formal systems in representing all mathematical truths.
Conclusion and Future Perspectives
Turing completeness establishes a framework for computational universality, yet the Halting problem reveals inherent limitations in algorithmic predictability, proving that certain computations cannot be decided by any Turing machine. Future research aims to explore alternative computational models, such as quantum computing and hypercomputation, which may transcend classical constraints highlighted by the Halting problem. Advancements in formal methods and verification techniques seek to mitigate undecidability issues in practical applications despite theoretical boundaries.
Turing completeness Infographic
 libterm.com
libterm.com