Jordan algebra is a non-associative algebraic structure that generalizes certain properties of associative algebras, focusing on a commutative product satisfying the Jordan identity. It plays a crucial role in various fields such as quantum mechanics, projective geometry, and differential geometry, providing a framework for studying observables and symmetries. Explore the rest of this article to deepen your understanding of Jordan algebra and its significant applications across mathematics and physics.
Table of Comparison
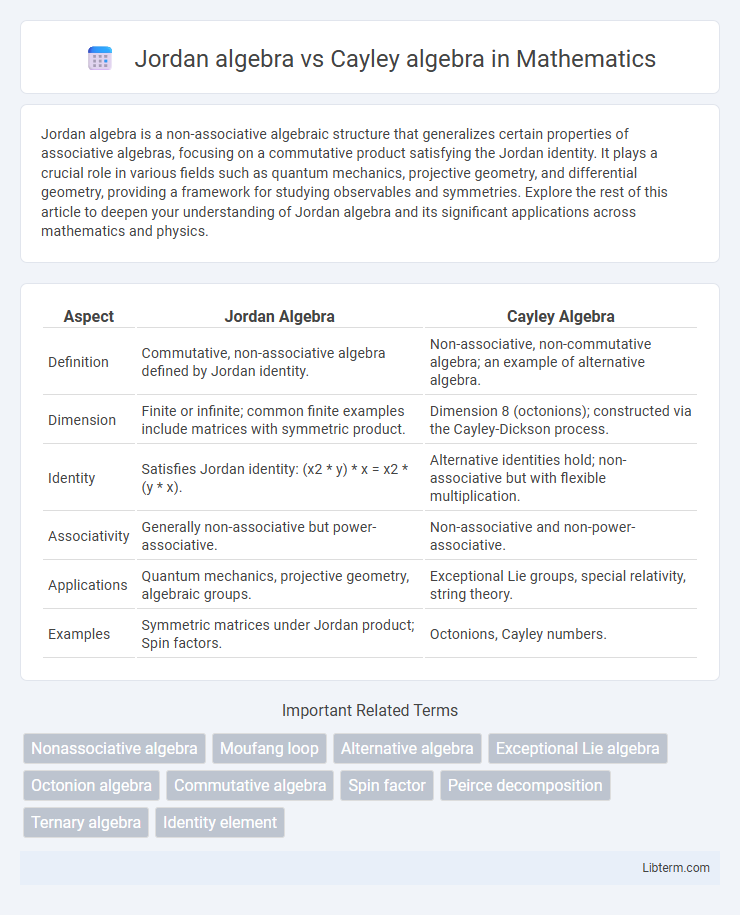
| Aspect | Jordan Algebra | Cayley Algebra |
|---|---|---|
| Definition | Commutative, non-associative algebra defined by Jordan identity. | Non-associative, non-commutative algebra; an example of alternative algebra. |
| Dimension | Finite or infinite; common finite examples include matrices with symmetric product. | Dimension 8 (octonions); constructed via the Cayley-Dickson process. |
| Identity | Satisfies Jordan identity: (x2 * y) * x = x2 * (y * x). | Alternative identities hold; non-associative but with flexible multiplication. |
| Associativity | Generally non-associative but power-associative. | Non-associative and non-power-associative. |
| Applications | Quantum mechanics, projective geometry, algebraic groups. | Exceptional Lie groups, special relativity, string theory. |
| Examples | Symmetric matrices under Jordan product; Spin factors. | Octonions, Cayley numbers. |
Introduction to Jordan Algebras
Jordan algebras, introduced by Pascual Jordan in 1933, are non-associative algebras primarily used to formalize observables in quantum mechanics, characterized by the Jordan identity: \( (A^2 \circ B) \circ A = A^2 \circ (B \circ A) \). Unlike Cayley algebras (or octonions), which are non-associative normed division algebras used in certain geometric and algebraic constructions, Jordan algebras emphasize commutative but non-associative products preserving symmetry and allowing a generalization of associative algebras. Their development enabled advances in operator theory and quantum physics by providing a flexible algebraic framework that captures symmetric bilinear operations without requiring associativity.
Introduction to Cayley Algebras
Cayley algebras, also known as octonion algebras, are non-associative normed division algebras extending quaternions with eight-dimensional structure over a field. Unlike Jordan algebras, which are commutative but generally non-associative algebras used mainly in quantum mechanics and projective geometry, Cayley algebras exhibit alternative, flexible multiplication properties crucial for modeling exceptional Lie groups and certain aspects of string theory. The unique composition and multiplication rules of Cayley algebras enable rich algebraic and geometric interpretations distinct from the symmetric and power-associative characteristics of Jordan algebras.
Historical Development and Origins
Jordan algebras originated in the 1930s through the work of Pascual Jordan, who sought to formalize observables in quantum mechanics, leading to a commutative but non-associative algebra structure. Cayley algebras, also known as octonion algebras, trace back to Arthur Cayley's 19th-century exploration of normed division algebras, characterized by their non-associative, alternative property and connection to eight-dimensional number systems. The historical development of Jordan algebras is rooted in mathematical physics, whereas Cayley algebras emerged from algebraic generalizations of quaternion numbers within pure mathematics.
Mathematical Definitions and Structures
Jordan algebra is a commutative, non-associative algebra defined by the Jordan identity \((x \circ y) \circ x^2 = x \circ (y \circ x^2)\), where the product \( \circ \) is symmetric and satisfies bilinearity. Cayley algebra, also known as the octonions, forms an eight-dimensional non-associative algebra over the real numbers characterized by the property of alternative multiplication and the presence of a norm form that satisfies \(N(xy)=N(x)N(y)\). While Jordan algebras arise from symmetrizing associative algebras to generalize quantum mechanics observables, Cayley algebras generalize quaternionic structures with non-associativity governed by the Moufang identities.
Key Properties and Operations
Jordan algebras are commutative but generally non-associative algebras characterized by the Jordan identity, emphasizing symmetric bilinear forms and quadratic operations essential in quantum mechanics and projective geometry. Cayley algebras, or octonion algebras, are non-associative and non-commutative but alternative, featuring a normed division algebra structure with a multiplicative quadratic form and a Moufang loop property. Key operations in Jordan algebras include the Jordan product defined by symmetrizing the usual product, whereas Cayley algebras rely on non-associative multiplication with composition and conjugation operations crucial for their division algebra properties.
Examples and Applications
Jordan algebras, exemplified by the algebra of self-adjoint operators on a Hilbert space, are widely applied in quantum mechanics for modeling observables and state spaces. Cayley algebras, also known as octonions, are non-associative algebras with applications in theoretical physics, particularly in string theory and special relativity due to their exceptional symmetry properties. Examples include the Albert algebra, a 27-dimensional exceptional Jordan algebra, and the 8-dimensional octonion algebra, both serving as foundational structures in advanced algebraic and physical theories.
Similarities Between Jordan and Cayley Algebras
Jordan algebras and Cayley algebras both arise in the study of non-associative algebraic structures with applications in physics and geometry. They share similarities such as the presence of a bilinear product and the role of composition properties that generalize associative multiplication. Both algebras are instrumental in understanding exceptional structures, with Jordan algebras linked to symmetric cones and Cayley algebras underpinning octonions and related division algebras.
Fundamental Differences
Jordan algebras are commutative, non-associative algebras primarily used in quantum mechanics and projective geometry, characterized by the Jordan identity (x2(yx) = x(yx2)). Cayley algebras, also known as octonion algebras, are non-associative and non-commutative division algebras extending quaternions, distinguished by their alternative property and a norm that allows composition. The fundamental difference lies in Jordan algebras emphasizing commutativity and flexible power-associativity, while Cayley algebras focus on non-commutativity with a norm structure enabling division algebra properties.
Roles in Modern Mathematics and Physics
Jordan algebras play a crucial role in modern mathematics and physics by providing algebraic frameworks for quantum mechanics observables, enabling the study of non-associative structures in operator theory and functional analysis. Cayley algebras, or octonions, contribute to the understanding of exceptional Lie groups, string theory, and special geometric structures through their non-associative and non-commutative properties, influencing theoretical physics and advanced algebraic geometry. Both algebras enrich the study of symmetry, helping to bridge algebraic concepts with physical phenomena in high-energy physics and quantum field theory.
Conclusion and Future Perspectives
Jordan algebras and Cayley algebras exhibit distinct algebraic structures with significant applications in theoretical physics and geometry, particularly in studying symmetry and particle physics. Advancements in understanding their role in non-associative algebras could lead to new mathematical frameworks for quantum mechanics and string theory. Future research should focus on exploring categorical equivalences and novel representations, potentially unveiling deeper relationships between these algebras and exceptional Lie groups.
Jordan algebra Infographic
 libterm.com
libterm.com