Holder continuity describes a function's smoothness by bounding the difference between its values with a power of the distance between points, ensuring controlled behavior even when differentiability fails. This property plays a crucial role in analyzing partial differential equations and fractal geometry, offering valuable insight into irregular yet stable structures. Discover how Holder continuity can enhance your understanding of mathematical analysis and its applications in the rest of this article.
Table of Comparison
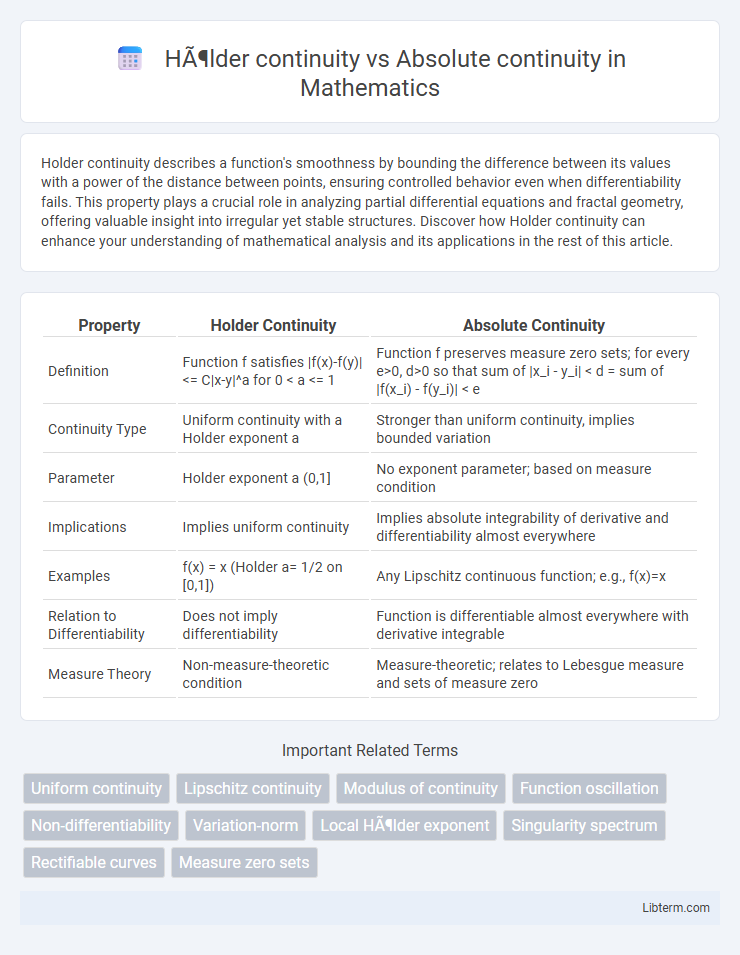
| Property | Holder Continuity | Absolute Continuity |
|---|---|---|
| Definition | Function f satisfies |f(x)-f(y)| <= C|x-y|^a for 0 < a <= 1 | Function f preserves measure zero sets; for every e>0, d>0 so that sum of |x_i - y_i| < d = sum of |f(x_i) - f(y_i)| < e |
| Continuity Type | Uniform continuity with a Holder exponent a | Stronger than uniform continuity, implies bounded variation |
| Parameter | Holder exponent a (0,1] | No exponent parameter; based on measure condition |
| Implications | Implies uniform continuity | Implies absolute integrability of derivative and differentiability almost everywhere |
| Examples | f(x) = x (Holder a= 1/2 on [0,1]) | Any Lipschitz continuous function; e.g., f(x)=x |
| Relation to Differentiability | Does not imply differentiability | Function is differentiable almost everywhere with derivative integrable |
| Measure Theory | Non-measure-theoretic condition | Measure-theoretic; relates to Lebesgue measure and sets of measure zero |
Introduction to Continuity in Mathematical Analysis
Holder continuity generalizes the concept of uniform continuity by requiring that the difference between function values is bounded by a fixed multiple of the distance between points raised to a power a (0 < a <= 1), enabling analysis of functions with controlled but non-linear smoothness. Absolute continuity strengthens this notion by demanding that for every e > 0, there exists d > 0 such that the total variation of the function over any collection of intervals with a combined length less than d is less than e, ensuring properties like differentiability almost everywhere and integrability of the derivative. These continuity types play crucial roles in mathematical analysis, particularly in measure theory and differential equations, by characterizing function regularity beyond basic continuity and uniform continuity.
Defining Hölder Continuity
Holder continuity defines a function \( f \) on a metric space where there exist constants \( C > 0 \) and \( 0 < \alpha \leq 1 \) such that for every pair of points \( x \) and \( y \), the inequality \(|f(x) - f(y)| \leq C |x - y|^\alpha\) holds, indicating a controlled rate of variation. This condition generalizes Lipschitz continuity by allowing the exponent \(\alpha\) to be less than 1, capturing functions with smoother behavior than mere continuity but potentially less restrictive than Lipschitz continuous functions. Holder continuous functions are crucial in various areas of analysis and partial differential equations, where the degree of smoothness affects existence and uniqueness of solutions.
Exploring Absolute Continuity
Absolute continuity is a stronger form of continuity that implies Holder continuity but requires that the function's variation on any interval is controlled by the length of that interval, ensuring integrable derivative behavior. Functions that are absolutely continuous possess a derivative almost everywhere, and the function can be recovered by integrating this derivative, making them central to measure theory and real analysis. This property is essential in the fundamental theorem of calculus and differentiates from Holder continuous functions, which may be continuous but need not have integrable derivatives or satisfy the absolute continuity condition.
Key Differences Between Hölder and Absolute Continuity
Holder continuity requires a function \( f \) to satisfy the inequality \( |f(x) - f(y)| \leq C|x - y|^\alpha \) for some constants \( C > 0 \) and \( 0 < \alpha \leq 1 \), emphasizing control over local oscillations with a fractional exponent \(\alpha\). Absolute continuity is a stronger condition, ensuring that for every \(\epsilon > 0\), there exists \(\delta > 0\) such that the sum of lengths of disjoint intervals \(\{(a_k,b_k)\}\) with total length less than \(\delta\) implies the sum of \( |f(b_k)-f(a_k)| < \epsilon\), linking closely to the function's integrability and differentiability almost everywhere. Unlike Holder continuity, absolute continuity guarantees the existence of a derivative almost everywhere and the function can be recovered by integrating its derivative, establishing a fundamental link in real analysis and measure theory.
Mathematical Formulations and Criteria
Holder continuity for a function f involves the existence of constants C > 0 and a (0,1] such that |f(x) - f(y)| <= C|x - y|^a holds for all x, y in the domain, emphasizing controlled local oscillations with exponent a. Absolute continuity requires that for every e > 0, there exists d > 0 ensuring the sum of lengths of disjoint intervals in the domain less than d implies the sum of the absolute differences of f over those intervals is less than e; it implies differentiability almost everywhere with the function represented as an integral of its derivative. Holder continuity is a pointwise regularity condition focused on local behavior, while absolute continuity is a global property linked to measure theory and the fundamental theorem of calculus.
Examples Illustrating Hölder Continuity
Holder continuity describes functions where differences satisfy a bound of the form |f(x) - f(y)| <= C|x - y|^a for some a (0,1], illustrating controlled but potentially non-linear smoothness. Classic examples include the Weierstrass function, which is Holder continuous with exponent a < 1 but not differentiable, showcasing fractal-like behavior, and functions like f(x) = x on [0,1], demonstrating Holder continuity with a = 1/2. In contrast, absolute continuity implies stronger regularity with integral representation and differentiability almost everywhere, placing Holder continuity examples in a broader context of function smoothness hierarchy.
Practical Instances of Absolute Continuity
Absolute continuity ensures that functions like cumulative distribution functions in probability theory have derivatives almost everywhere and preserve measure zero sets, making them crucial in real analysis and measure theory. Practical instances include the integration of Lebesgue integrable functions and solutions to differential equations where smooth behavior and precise control over variations are required. Holder continuity, in contrast, deals with local smoothness and rate of change but does not guarantee the stronger measure-theoretic properties inherent in absolutely continuous functions.
Relationship with Lipschitz Continuity
Holder continuity generalizes Lipschitz continuity by allowing the function's increments to be bounded by a power of the distance between points, specifically |f(x)-f(y)| <= C|x-y|^a for 0 < a <= 1, where a=1 corresponds exactly to Lipschitz continuity. Absolute continuity implies Lipschitz continuity on compact intervals when the derivative is bounded, linking the concepts through integrability and differentiability properties. While all Lipschitz continuous functions are absolutely continuous, not all absolutely continuous functions are Lipschitz, and Holder continuity provides an intermediate regularity scale positioned between continuity and Lipschitz continuity.
Implications in Real Analysis and Applications
Holder continuity implies a controlled rate of change with a specific exponent, crucial for ensuring the stability of solutions in partial differential equations and fractal geometry. Absolute continuity guarantees the existence of a derivative almost everywhere and is fundamental for the validity of the Fundamental Theorem of Calculus in measure theory and integration. While absolute continuity implies uniform continuity and differentiability almost everywhere, Holder continuity does not necessarily ensure differentiability, highlighting their distinct roles in real analysis and applications.
Summary and Comparative Insights
Holder continuity defines a function's smoothness by bounding the difference between function values with a power of the distance between points, characterized by a Holder exponent \( \alpha \in (0,1] \), ensuring controlled local oscillations but not necessarily differentiability. Absolute continuity is a stronger condition implying both uniform continuity and differentiability almost everywhere, guaranteeing that the function's behavior can be recovered from its derivative via the Fundamental Theorem of Calculus. Compared to Holder continuity, absolute continuity ensures integrability and stronger regularity properties, making it crucial in measure theory and real analysis for functions with integrable derivatives.
Hölder continuity Infographic
 libterm.com
libterm.com