A measurable set is a fundamental concept in measure theory, defining sets for which a consistent measure, such as length, area, or volume, can be assigned. These sets enable the rigorous integration and probability calculations vital to analysis and applied mathematics. Explore the rest of the article to understand how measurable sets shape mathematical frameworks and impact various fields.
Table of Comparison
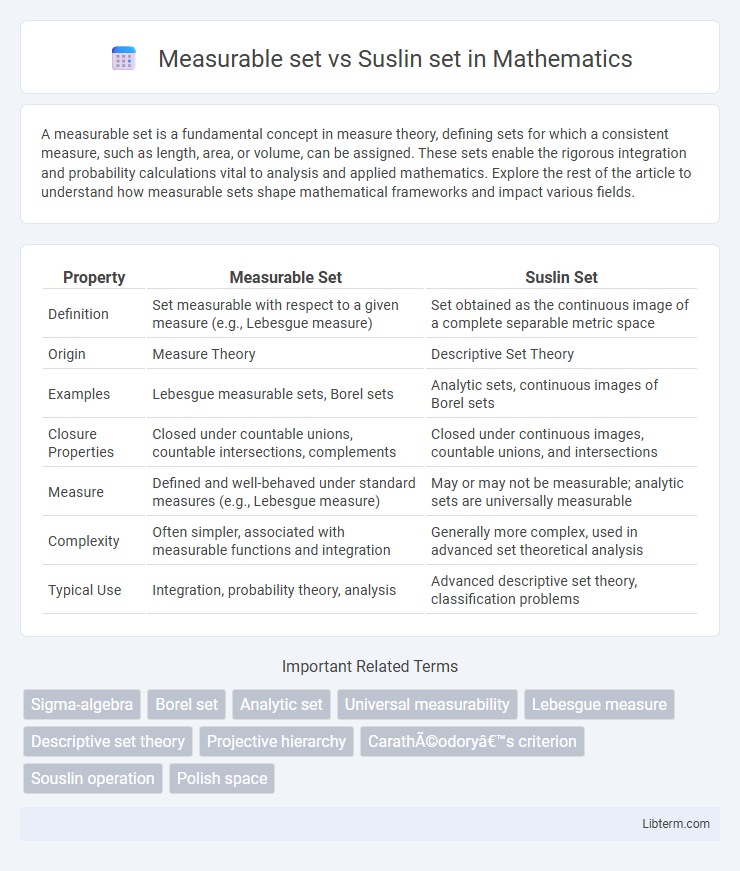
| Property | Measurable Set | Suslin Set |
|---|---|---|
| Definition | Set measurable with respect to a given measure (e.g., Lebesgue measure) | Set obtained as the continuous image of a complete separable metric space |
| Origin | Measure Theory | Descriptive Set Theory |
| Examples | Lebesgue measurable sets, Borel sets | Analytic sets, continuous images of Borel sets |
| Closure Properties | Closed under countable unions, countable intersections, complements | Closed under continuous images, countable unions, and intersections |
| Measure | Defined and well-behaved under standard measures (e.g., Lebesgue measure) | May or may not be measurable; analytic sets are universally measurable |
| Complexity | Often simpler, associated with measurable functions and integration | Generally more complex, used in advanced set theoretical analysis |
| Typical Use | Integration, probability theory, analysis | Advanced descriptive set theory, classification problems |
Definition of Measurable Sets
Measurable sets are defined within the framework of a sigma-algebra, typically generated by open or closed sets, ensuring the assignment of a consistent measure such as the Lebesgue measure. These sets satisfy countable additivity and closure under complements, enabling integration and probability calculations. In contrast, Suslin sets, arising from analytic set theory, extend beyond measurable sets by being images of Borel sets under continuous mappings but may lack straightforward measure assignments.
Definition of Suslin Sets
Suslin sets, also known as analytic sets, are defined as continuous images of Borel sets in Polish spaces, making them a crucial class within descriptive set theory. Unlike measurable sets, which are defined primarily through sigma-algebras and measure functions, Suslin sets rely on topological and operational constructs, specifically the operation of Suslin's operation (or A-operation) applied to closed sets. This approach enables Suslin sets to generalize Borel sets while maintaining key regularity properties, such as the perfect set property and universal measurability.
Historical Background of Set Theory
Measurable sets emerged from early 20th-century efforts to formalize integration theory, notably through Henri Lebesgue's work on measure and measurable functions in 1902. Suslin sets, introduced by Mikhail Suslin in 1917, arose from investigations into the analytic hierarchy and descriptive set theory, addressing limitations in Borel set characterization. These developments collectively shaped modern set theory by expanding the classification and analysis of complex subsets within Polish spaces.
Properties of Measurable Sets
Measurable sets, particularly in the context of Lebesgue measure, are characterized by properties such as countable additivity, completeness, and closure under countable unions and intersections, ensuring robust integration and limit operations. Unlike Suslin sets, which are derived from analytic sets through Suslin's operation and pertain to descriptive set theory, measurable sets maintain compatibility with sigma-algebras and measure functions, allowing precise quantification of size and probability. The measurability property guarantees that measurable sets can be approximated from inside and outside by open or closed sets, facilitating practical applications in real analysis and probability theory.
Properties of Suslin Sets
Suslin sets, also known as analytic sets, are defined as continuous images of Borel sets from Polish spaces and exhibit closure under continuous mappings, countable unions, and intersections. Unlike measurable sets, Suslin sets may not always be Lebesgue measurable but possess the property of being universally measurable and have the Baire property. Their structural complexity places them strictly between Borel sets and all projective sets, making them crucial in descriptive set theory and the study of definability in Polish spaces.
Key Differences Between Measurable and Suslin Sets
Measurable sets are defined within a sigma-algebra, typically involving Lebesgue measure, ensuring that their measure is well-defined and obeys countable additivity; Suslin sets, on the other hand, arise from descriptive set theory as projections of Borel sets, often characterized by their analytic properties rather than measure. A key difference lies in measurability: all measurable sets have measure-theoretic regularity, while not all Suslin sets are measurable, although every Suslin set is universally measurable under certain measures. Furthermore, measurable sets are fundamental in integration and probability, whereas Suslin sets play a critical role in classification problems and hierarchy structures within Polish spaces.
Measurability Criteria and Conditions
Measurable sets are defined by satisfying specific criteria such as adherence to a sigma-algebra, closure under countable unions, intersections, and complements, ensuring well-defined measures like Lebesgue measure. Suslin sets, generated from continuous images of Borel sets, are analytic and universally measurable but may not lie within any given sigma-algebra, complicating traditional measurability verification. The measurability conditions for Suslin sets hinge on their construction via Suslin operations (A-operations) and utilize descriptive set theory, contrasting with measurable sets characterized by classical measure-theoretic axioms.
Role of Suslin Sets in Descriptive Set Theory
Suslin sets play a crucial role in descriptive set theory as they generalize Borel sets and are created through operations involving continuous images of Borel sets, bridging the gap between measurable and analytic sets. While measurable sets are defined via sigma-algebras and measure theory, Suslin sets are characterized by Suslin schemes, enabling a finer classification of definable sets beyond classical Borel hierarchies. This allows researchers to analyze complex hierarchies of definable sets, particularly in Polish spaces, expanding the scope of measurable set theory through descriptive set-theoretic techniques.
Applications of Measurable and Suslin Sets
Measurable sets are fundamental in probability theory and integration, enabling precise calculations of probabilities, expectations, and Lebesgue integrals in real analysis and stochastic processes. Suslin sets, defined via continuous images of Borel sets, play a crucial role in descriptive set theory and functional analysis, particularly in the study of analytic sets and their properties in Polish spaces. Applications of measurable sets include defining measurable functions and sigma-algebras for probability spaces, while Suslin sets are essential in classifying complex sets and exploring topological properties in advanced mathematical analysis.
Open Problems and Further Research Directions
The distinction between measurable sets and Suslin sets remains a central focus in descriptive set theory, with open problems concerning their characterization under various models of set theory. Research continues to explore the extent to which every Suslin set is measurable, especially in non-classical frameworks or under large cardinal assumptions. Further investigation targets the interaction between Suslin operations, regularity properties, and definability, aiming to bridge gaps between measure theory, topology, and effective descriptive set theory.
Measurable set Infographic
 libterm.com
libterm.com