Permutation groups are mathematical structures that describe symmetries by representing all possible arrangements of a set's elements. They play a crucial role in fields like algebra, combinatorics, and cryptography, providing a framework to analyze transformations and their properties. Explore the rest of the article to deepen Your understanding of permutation groups and their diverse applications.
Table of Comparison
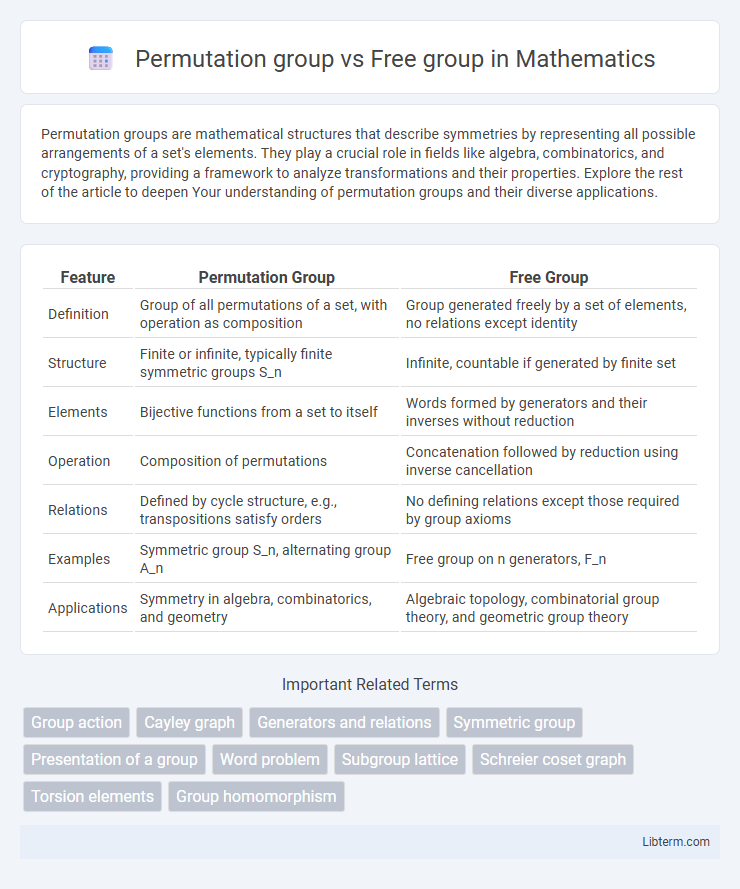
| Feature | Permutation Group | Free Group |
|---|---|---|
| Definition | Group of all permutations of a set, with operation as composition | Group generated freely by a set of elements, no relations except identity |
| Structure | Finite or infinite, typically finite symmetric groups S_n | Infinite, countable if generated by finite set |
| Elements | Bijective functions from a set to itself | Words formed by generators and their inverses without reduction |
| Operation | Composition of permutations | Concatenation followed by reduction using inverse cancellation |
| Relations | Defined by cycle structure, e.g., transpositions satisfy orders | No defining relations except those required by group axioms |
| Examples | Symmetric group S_n, alternating group A_n | Free group on n generators, F_n |
| Applications | Symmetry in algebra, combinatorics, and geometry | Algebraic topology, combinatorial group theory, and geometric group theory |
Introduction to Permutation Groups and Free Groups
Permutation groups consist of all bijections of a set onto itself under composition, representing symmetries and providing foundational examples in group theory. Free groups are generated by a set without relations, embodying the most general non-abelian groups and serving as building blocks for constructing other groups. Both structures play crucial roles in algebra, with permutation groups modeling concrete symmetries and free groups facilitating abstract group presentations.
Fundamental Definitions and Concepts
Permutation groups consist of all bijective functions from a set onto itself, with group operation defined as composition, emphasizing the rearrangement of elements and structure preservation. Free groups are generated by a set of elements with no relations other than the group axioms, characterized by unique reduced word representations and capturing the idea of infinite, unrestricted combinations. The fundamental difference lies in permutation groups encoding symmetries via element arrangements, while free groups represent abstract algebraic freedom through generators and reduced words.
Algebraic Structure: Permutation vs Free Groups
Permutation groups consist of bijections on a set with composition as the group operation, embodying a concrete algebraic structure where elements correspond to rearrangements of objects. Free groups, generated by a set without imposed relations other than group axioms, represent the most general type of non-abelian groups, allowing elements to be expressed uniquely as reduced words over the generators. While permutation groups are finite or countably infinite and represent symmetries explicitly, free groups are infinite in rank and serve as fundamental building blocks in combinatorial and geometric group theory.
Generators and Relations in Both Groups
Permutation groups are generated by a finite set of permutations with relations determined by the group's operation and the specific cycle structures, reflecting symmetry properties within the group. Free groups are generated by an arbitrary alphabet of symbols with no relations other than the group axioms, allowing words formed by generators and their inverses to represent distinct elements freely. The critical difference lies in permutation groups having defining relations that constrain generator combinations, whereas free groups impose no such restrictions, yielding maximal element diversity.
Examples of Permutation Groups
Permutation groups consist of sets of bijective functions that rearrange elements, exemplified by symmetric groups such as \( S_n \), which include all permutations of \( n \) distinct objects. The alternating group \( A_n \), a notable subgroup of \( S_n \), contains even permutations and plays a crucial role in group theory. In contrast to free groups generated by abstract symbols with no relations, permutation groups are concretely realized through actions on finite sets, making them central to fields like algebraic combinatorics and symmetry studies.
Examples of Free Groups
Free groups are algebraic structures generated by a set of elements subject to no relations other than the group axioms, exemplified by the free group on two generators, F2, consisting of all finite strings of the generators and their inverses with concatenation as the operation. Unlike permutation groups, which act on sets by rearranging elements and have rich symmetry structures, free groups emphasize unrestricted word formation. Classic examples include the free group on one generator, isomorphic to the integers under addition, and the free group on multiple generators, fundamental in combinatorial group theory and topology.
Key Properties and Differences
Permutation groups consist of elements representing bijections on a set, characterized by closure under composition, existence of inverses, and associativity, making them concrete examples of groups with finite or infinite order. Free groups, on the other hand, are defined by generators and relations with no imposed relations besides the group axioms, resulting in a highly non-abelian and universal structure. Key differences include the permutation group's dependence on set action and explicit symmetries, while free groups emphasize algebraic freedom and minimal constraints, leading to distinct applications in group theory and topology.
Applications in Mathematics and Beyond
Permutation groups, fundamental in algebra, model symmetries and are crucial in combinatorics, group theory, and cryptography due to their finite structure and concrete representations. Free groups, characterized by their lack of relations among generators, play a key role in topology, geometric group theory, and algebraic structures, enabling the study of fundamental groups of spaces and universal properties. Applications extend beyond pure mathematics into physics, computer science, and robotics, where permutation groups aid in symmetry analysis and free groups contribute to pathfinding and robotic motion planning.
Group Homomorphisms and Isomorphisms
Permutation groups, consisting of bijections on a set, exemplify finite symmetric structures where group homomorphisms preserve element order and cycle structure through conjugation. Free groups, generated by a set with no relations except identity reduction, admit homomorphisms defined uniquely by images of generators, reflecting universal mapping properties. Isomorphisms between free groups and permutation groups are constrained by structural rigidity and cardinality, with free groups often acting as universal covers while permutation groups exhibit concrete symmetry representations.
Conclusion: Comparing Permutation Groups and Free Groups
Permutation groups consist of all bijections on a finite set, characterized by well-defined compositions and relations, enabling precise algebraic manipulations. Free groups, generated by a set without imposing relations beyond group axioms, allow infinite reduced words and provide a foundational model for group theory and topological applications. Comparing these structures highlights that permutation groups represent concrete symmetries with specific constraints, while free groups offer universal, relation-free frameworks critical for understanding group presentations and algebraic freedom.
Permutation group Infographic
 libterm.com
libterm.com