Finite refers to something having limits or bounds, often contrasting with infinite or limitless concepts. In mathematics, finite sets contain a specific number of elements, which impacts problem-solving and computational methods. Explore the rest of the article to understand how finite principles affect various fields and your daily decision-making.
Table of Comparison
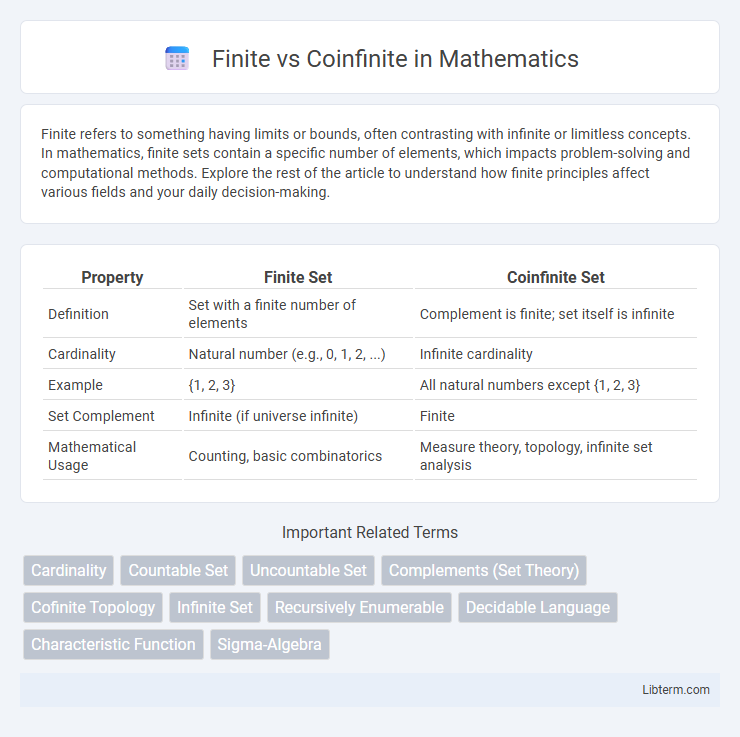
| Property | Finite Set | Coinfinite Set |
|---|---|---|
| Definition | Set with a finite number of elements | Complement is finite; set itself is infinite |
| Cardinality | Natural number (e.g., 0, 1, 2, ...) | Infinite cardinality |
| Example | {1, 2, 3} | All natural numbers except {1, 2, 3} |
| Set Complement | Infinite (if universe infinite) | Finite |
| Mathematical Usage | Counting, basic combinatorics | Measure theory, topology, infinite set analysis |
Introduction to Finite and Coinfinite Concepts
Finite sets contain a limited number of elements, allowing for exact enumeration and straightforward manipulation in mathematical and computational contexts. Coinfinite sets, defined as subsets whose complements are finite within an infinite universal set, exhibit unique properties crucial in set theory and logic, especially in analyzing infinite structures. Understanding the distinction between finite and coinfinite sets enhances the study of infinite cardinalities and their applications in topology, measure theory, and theoretical computer science.
Defining Finite Sets
Finite sets contain a countable number of elements that can be explicitly listed or matched one-to-one with a subset of natural numbers. Defining finite sets involves establishing a clear boundary on the number of elements, ensuring the set is not infinite or uncountably large. Understanding finite sets serves as a foundational concept in set theory, contrasting with coinfinite sets whose complements are finite.
Understanding Coinfinite Sets
Coinfinite sets refer to infinite sets whose complements within a universal set are finite, meaning that only finitely many elements are excluded. Understanding coinfinite sets involves recognizing their role in set theory as complements of finite sets, which helps illustrate properties of infinite cardinalities and the structure of infinite subsets. These sets are fundamental in discussions of topology, measure theory, and logic since their complements' finiteness imparts distinctive behavioral and definitional characteristics.
Key Differences: Finite vs Coinfinite
Finite sets contain a limited number of elements, while coinfinite sets have infinitely many elements complementary to a finite subset within an infinite universal set. The key difference lies in cardinality: finite sets have a countable size, whereas coinfinite sets are defined by the property that their complements in an infinite universe are finite. This distinction impacts set operations and mathematical properties in topology and measure theory.
Mathematical Examples of Finite Sets
Finite sets in mathematics include examples such as the set of natural numbers less than 10, {1, 2, 3, 4, 5, 6, 7, 8, 9}, or the set of letters in the English alphabet, {A, B, C, ..., Z}. These sets contain a countable number of elements that can be explicitly listed or enumerated. Contrastingly, co-infinite sets are infinite sets whose complements within a larger set are finite, illustrating different measure and cardinality properties in set theory.
Illustrative Examples of Coinfinite Sets
Coinfinite sets are characterized by having complements that are finite, exemplified by the set of all natural numbers except a finite subset such as {1, 2, 3}. Another illustrative example is the set of integers excluding a finite number of specific values, like excluding {-1, 0, 1}, which remains coinfinite since infinitely many integers remain. These examples highlight the distinction between finite and coinfinite sets, essential in understanding infinite set theory and its applications in topology and measure theory.
Applications in Mathematics and Computer Science
Finite sets, characterized by a countable number of elements, are central to algorithm design, complexity analysis, and data structure optimization in computer science, ensuring predictable resource usage and efficient computation. Coinfinite sets, whose complements are finite, play a crucial role in formal language theory, automata, and infinite sequence analysis, enabling the study of system behaviors approaching completeness or infinity. Mathematical applications include topology and measure theory, where finite and coinfinite distinctions facilitate the classification of sets and the understanding of properties like convergence and density.
Importance in Set Theory
Finite and cofinite sets play a crucial role in set theory by providing fundamental examples that illustrate concepts of cardinality and complementarity. A finite set contains a limited number of elements, while a cofinite set's complement is finite, highlighting the duality between sets and their complements. Understanding these distinctions is essential for grasping topological properties, constructing filters, and analyzing sigma-algebras within mathematical structures.
Common Misconceptions
Finite sets contain a limited number of elements, while cofinite sets have complements that are finite, often causing confusion in set theory. A common misconception is assuming cofinite sets are infinite, but they can include all but a finite number of elements, making their size context-dependent. Understanding the distinction is crucial for accurate analysis in topology and discrete mathematics.
Conclusion: Comparing Finite and Coinfinite
Finite sets contain a limited number of elements, making them countable and often easier to analyze within discrete mathematics. Coinfinite sets, being infinite complements of finite sets within a larger infinite set, exhibit properties that challenge typical finite constraints and require advanced techniques in set theory. Comparing finite and coinfinite sets highlights fundamental differences in cardinality and mathematical behavior, crucial for understanding infinite structures and their applications in logic and computation.
Finite Infographic
 libterm.com
libterm.com