A semisimple module is a module that can be expressed as a direct sum of simple submodules, making its structure completely reducible. Such modules are crucial in representation theory and abstract algebra due to their well-understood and highly decomposable nature. Explore the rest of the article to deepen your understanding of semisimple modules and their applications.
Table of Comparison
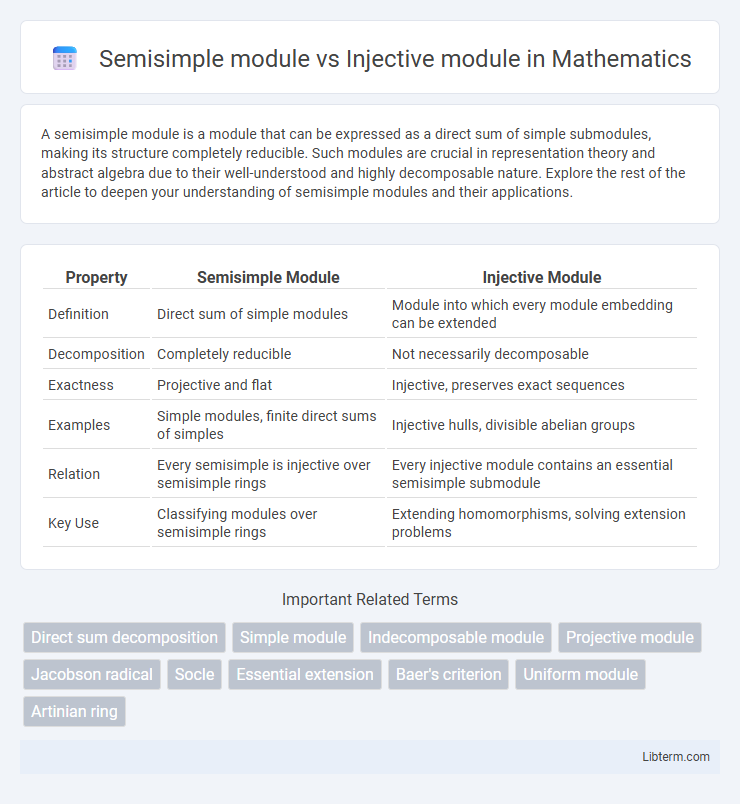
| Property | Semisimple Module | Injective Module |
|---|---|---|
| Definition | Direct sum of simple modules | Module into which every module embedding can be extended |
| Decomposition | Completely reducible | Not necessarily decomposable |
| Exactness | Projective and flat | Injective, preserves exact sequences |
| Examples | Simple modules, finite direct sums of simples | Injective hulls, divisible abelian groups |
| Relation | Every semisimple is injective over semisimple rings | Every injective module contains an essential semisimple submodule |
| Key Use | Classifying modules over semisimple rings | Extending homomorphisms, solving extension problems |
Introduction to Modules in Algebra
Semisimple modules are direct sums of simple modules, characterized by having no nontrivial submodules, which makes them completely reducible and fundamental in the study of module decompositions. Injective modules, defined by their extension property allowing any homomorphism from a submodule to extend to the whole module, play a crucial role in homological algebra and module theory. Understanding the distinction between semisimple and injective modules is essential for exploring module classification, homological dimensions, and decomposition theorems in algebra.
Defining Semisimple Modules
Semisimple modules are defined as modules that can be expressed as a direct sum of simple submodules, where each simple submodule has no proper nonzero submodules. This property ensures that semisimple modules are completely reducible, making them fundamental in the structure theory of modules over rings. In contrast, injective modules are characterized by their extension property, where any homomorphism defined on a submodule can be extended to the entire module, highlighting a key difference in their categorical behavior.
Defining Injective Modules
Injective modules are defined by their property that every homomorphism from a submodule of any module extends to a homomorphism from the entire module. They can be characterized as modules that are direct summands of every module containing them as a submodule. In contrast, semisimple modules decompose into simple modules but lack the universal extension property that defines injective modules.
Structural Properties of Semisimple Modules
Semisimple modules decompose into direct sums of simple modules, exhibiting a completely reducible structure that facilitates classification and analysis. These modules are characterized by their projective and injective properties, with every semisimple module being injective over a semisimple ring, ensuring extensibility and splitting of exact sequences. The structural rigidity of semisimple modules contrasts with general injective modules, which may lack decomposability but serve as essential objects in homological algebra for embedding and extension problems.
Structural Properties of Injective Modules
Injective modules possess the structural property of being direct summands in any module containing them, which contrasts with semisimple modules that decompose entirely into simple submodules. While semisimple modules are direct sums of simple modules and have well-understood decompositions, injective modules are characterized by their extension and lifting properties, allowing homomorphisms to extend over any embedding. This intrinsic extension property makes injective modules particularly essential in homological algebra, providing structural insights beyond the completely reducible nature of semisimple modules.
Key Differences Between Semisimple and Injective Modules
Semisimple modules are direct sums of simple modules, characterized by their complete decomposability into simple submodules, while injective modules are defined by their extension property that ensures any homomorphism into them can be extended from submodules. A key difference lies in their structural roles: semisimple modules exhibit a rigid, well-understood internal structure with every submodule having a complement, whereas injective modules serve primarily as objects allowing extension of homomorphisms, often containing complex submodule configurations without necessarily decomposing into simples. Moreover, every semisimple module is injective over semisimple rings, but injective modules need not be semisimple, highlighting distinct categorical and homological properties.
Examples of Semisimple and Injective Modules
Semisimple modules include examples such as vector spaces over fields and finite direct sums of simple modules, where each submodule is a direct summand. Injective modules are exemplified by divisible abelian groups like the rational numbers Q as a Z-module and injective hulls of simple modules, providing essential extensions in module theory. While all semisimple modules are injective over semisimple rings, injective modules have broader applications in homological algebra beyond the decomposition properties of semisimple modules.
Conditions for Semisimple and Injective Equivalence
Semisimple modules are characterized by being direct sums of simple modules, ensuring complete reducibility, while injective modules possess an extension property allowing homomorphisms to extend over larger modules. The equivalence of semisimple and injective modules occurs in specific rings, notably semisimple rings where every module is both projective and injective, such as in Artinian semisimple rings. Under these conditions, the category of modules exhibits perfect duality between decomposition and extension properties, making every injective module semisimple and vice versa.
Applications in Ring Theory and Homological Algebra
Semisimple modules decompose into direct sums of simple modules, providing a clear structure that simplifies the classification of modules over semisimple rings, which is crucial in representation theory and the study of Artinian rings. Injective modules, characterized by their extension properties, play a key role in homological algebra, particularly in constructing injective resolutions that facilitate the computation of Ext and Tor functors. In ring theory, injective modules aid in understanding module extensions and splitting conditions, while semisimple modules contribute to the analysis of completely reducible representations and the Wedderburn-Artin theorem.
Summary and Comparative Analysis
Semisimple modules are direct sums of simple modules characterized by complete reducibility, while injective modules possess an extension property ensuring any homomorphism from a submodule can be extended to the entire module. Semisimple modules exhibit projectivity and injectivity under certain ring conditions, such as semisimple rings, whereas injective modules generalize the concept of divisibility and contain all modules as submodules in their injective hulls. The key distinction lies in semisimple modules being decomposable into simple components, contrasted with injective modules emphasizing homomorphic extension and module completeness.
Semisimple module Infographic
 libterm.com
libterm.com