Complete space exploration uncovers vast opportunities and challenges beyond our planet, expanding scientific knowledge and technological innovation to unprecedented levels. Understanding the intricacies of cosmic environments and human adaptation is essential for future missions to distant worlds. Dive deeper into this comprehensive guide to discover how your curiosity can be part of humanity's next giant leap.
Table of Comparison
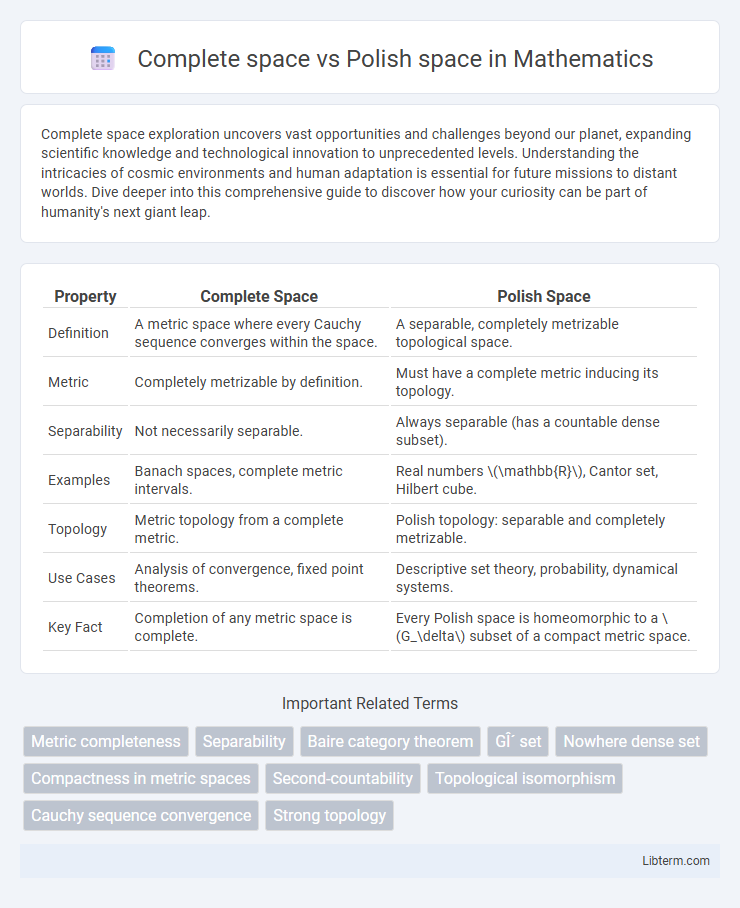
| Property | Complete Space | Polish Space |
|---|---|---|
| Definition | A metric space where every Cauchy sequence converges within the space. | A separable, completely metrizable topological space. |
| Metric | Completely metrizable by definition. | Must have a complete metric inducing its topology. |
| Separability | Not necessarily separable. | Always separable (has a countable dense subset). |
| Examples | Banach spaces, complete metric intervals. | Real numbers \(\mathbb{R}\), Cantor set, Hilbert cube. |
| Topology | Metric topology from a complete metric. | Polish topology: separable and completely metrizable. |
| Use Cases | Analysis of convergence, fixed point theorems. | Descriptive set theory, probability, dynamical systems. |
| Key Fact | Completion of any metric space is complete. | Every Polish space is homeomorphic to a \(G_\delta\) subset of a compact metric space. |
Introduction to Metric Spaces
A complete space is a metric space where every Cauchy sequence converges within the space, ensuring no "holes" in the structure. Polish spaces, defined as separable and completely metrizable spaces, combine completeness with a countable dense subset, making them fundamental in descriptive set theory and analysis. Understanding metric spaces involves grasping key concepts like distance functions, convergence, and completeness, which distinguish complete spaces and Polish spaces by their structural properties and applications.
Definition of Complete Space
A complete space is a metric space in which every Cauchy sequence converges to a limit that is within the space, ensuring no "gaps" in the structure. Polish spaces are a specific class of complete separable metric spaces, characterized by their completeness and the existence of a countable dense subset. This completeness property is fundamental for various areas in analysis, topology, and probability theory, providing a robust framework for convergence and continuity.
Definition of Polish Space
Polish space is defined as a separable completely metrizable topological space, meaning it has a metric under which it is complete and contains a countable dense subset. Complete space refers more generally to any metric space where every Cauchy sequence converges within the space, but it does not require separability. The distinction lies in Polish spaces combining completeness with separability, making them fundamental in descriptive set theory and analysis.
Key Properties of Complete Spaces
Complete spaces are metric or normed spaces where every Cauchy sequence converges to a limit within the space, ensuring no "gaps" exist. Polish spaces, a subclass of complete metric spaces, are separable and completely metrizable, making them essential in descriptive set theory and probability. The completeness property guarantees stability under limits and supports fixed point theorems critical in functional analysis and topology.
Key Properties of Polish Spaces
Polish spaces are complete separable metric spaces, meaning they possess a metric that is both complete and allows a countable dense subset, distinguishing them within the broader class of complete spaces that may lack separability. Key properties of Polish spaces include their universality in descriptive set theory, as every Polish space is homeomorphic to a G_delta subset of a compact metric space, and they support rich measure-theoretic and topological structures essential for analysis. Their completeness ensures every Cauchy sequence converges, while separability facilitates tractable and effective analytical and probabilistic methods.
Differences Between Complete and Polish Spaces
Complete spaces require every Cauchy sequence to converge within the space, ensuring metric completeness without additional topological constraints. Polish spaces are separable completely metrizable spaces, combining completeness with a countable dense subset, which provides strong structural and topological properties. The key difference is that all Polish spaces are complete, but not all complete spaces are Polish, as completeness alone does not guarantee separability or the existence of a compatible metric making the space Polish.
Examples of Complete Spaces
Complete spaces include Euclidean spaces such as \(\mathbb{R}^n\) with the standard norm, where every Cauchy sequence converges within the space. Banach spaces, like the space of continuous functions \(C([0,1])\) with the sup norm, serve as classic examples of complete normed vector spaces. Polish spaces are complete separable metric spaces, exemplified by \(\mathbb{R}^n\) and separable Hilbert spaces like \(\ell^2\).
Examples of Polish Spaces
Polish spaces are complete separable metric spaces exemplified by the real numbers \(\mathbb{R}\) with the usual metric, the Cantor set, and the Hilbert cube. While every Polish space is a complete metric space with a countable dense subset, not all complete metric spaces are Polish, as some may lack separability. Classic examples such as the Baire space and separable Hilbert spaces highlight the key properties of Polish spaces used extensively in descriptive set theory and functional analysis.
Applications in Functional Analysis
Complete spaces, such as Banach and Hilbert spaces, are fundamental in functional analysis due to their guarantee of limit convergence for Cauchy sequences, enabling the application of fixed-point theorems and spectral theory. Polish spaces, which are separable and completely metrizable, provide a robust framework in descriptive set theory and stochastic processes, facilitating measurable selection theorems and ergodic theory. The interplay between completeness and separability in these spaces activates nuanced functional analysis tools essential in operator theory and probability.
Conclusion: Choosing Between Complete and Polish Spaces
Complete spaces ensure every Cauchy sequence converges, providing robust frameworks for analysis and metric space theory. Polish spaces, as separable complete metric spaces, combine completeness with countability conditions, enabling effective applications in descriptive set theory and probability. Selection depends on the need for separability and countability; Polish spaces suit contexts requiring a dense countable subset, while complete spaces are preferable when separability is not necessary.
Complete space Infographic
 libterm.com
libterm.com