Differentiable functions are fundamental in calculus, allowing for the calculation of precise rates of change and enabling optimization in various mathematical models. Understanding the concept of differentiability helps in analyzing smoothness and continuity of functions crucial for both theoretical and practical applications. Explore the rest of the article to deepen your insight into how differentiable properties influence complex problem-solving in mathematics.
Table of Comparison
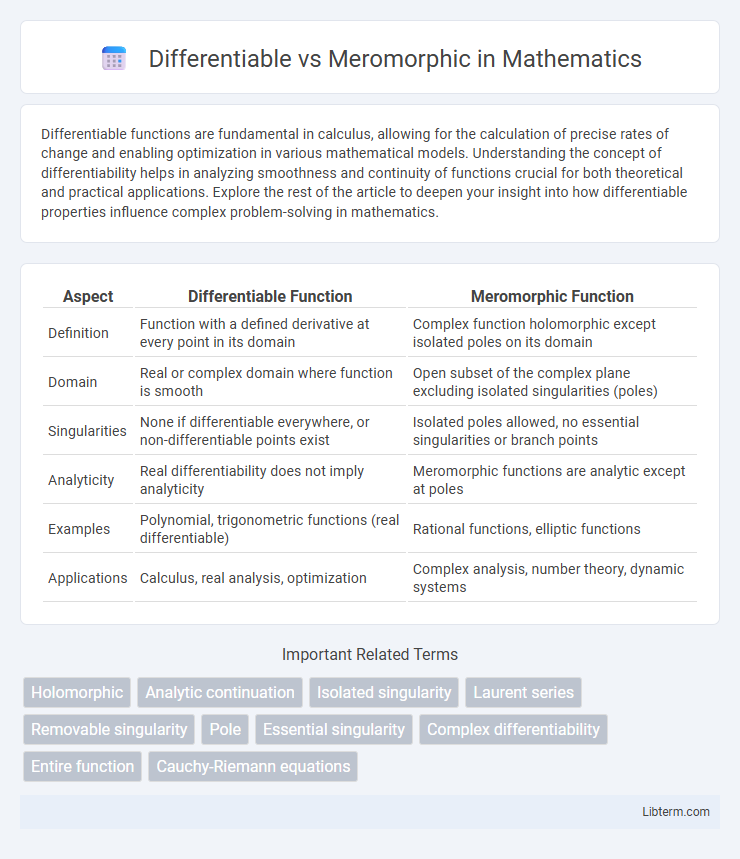
| Aspect | Differentiable Function | Meromorphic Function |
|---|---|---|
| Definition | Function with a defined derivative at every point in its domain | Complex function holomorphic except isolated poles on its domain |
| Domain | Real or complex domain where function is smooth | Open subset of the complex plane excluding isolated singularities (poles) |
| Singularities | None if differentiable everywhere, or non-differentiable points exist | Isolated poles allowed, no essential singularities or branch points |
| Analyticity | Real differentiability does not imply analyticity | Meromorphic functions are analytic except at poles |
| Examples | Polynomial, trigonometric functions (real differentiable) | Rational functions, elliptic functions |
| Applications | Calculus, real analysis, optimization | Complex analysis, number theory, dynamic systems |
Understanding Differentiable Functions
Differentiable functions are types of functions that possess derivatives at every point within their domain, enabling the measurement of instantaneous rates of change and local linear approximations. In complex analysis, these functions are holomorphic, meaning they are complex differentiable in an open set, which implies analyticity and infinite differentiability. Understanding the distinction between differentiable and meromorphic functions hinges on the presence of poles in meromorphic functions, where meromorphic functions allow isolated singularities while differentiable (holomorphic) functions are smooth and free of such singularities.
Defining Meromorphic Functions
Meromorphic functions are complex functions that are holomorphic throughout their domain except for isolated poles, where they exhibit singularities characterized by finite-order poles rather than essential singularities. Differentiable functions in the complex sense, or holomorphic functions, are infinitely differentiable and have no singularities within their domain. Understanding meromorphic functions requires analyzing their Laurent series expansions near poles, distinguishing them from merely differentiable functions by the presence of these well-defined singularities.
Key Differences: Differentiable vs Meromorphic
Differentiable functions are defined on real or complex domains where derivatives exist at every point, enabling smooth behavior and local linear approximations. Meromorphic functions, a subset of complex functions, are holomorphic throughout their domain except for isolated poles where they have well-defined singularities. The key difference lies in differentiability across the domain: differentiable functions possess derivatives everywhere, while meromorphic functions allow certain isolated points of non-differentiability characterized by poles.
Analyticity and Its Role
Differentiable functions in complex analysis are holomorphic, exhibiting complex differentiability at every point in their domain, ensuring analyticity and the existence of convergent power series expansions. Meromorphic functions extend this concept by allowing isolated poles, which are singularities where the function's behavior diverges, yet remain analytic elsewhere in the complex plane. Analyticity in differentiable functions guarantees smooth, complex structure, while in meromorphic functions it governs the controlled growth and behavior near singularities, making both crucial in complex function theory and its applications.
Poles and Singularities Explained
Differentiable functions are smooth and continuous, allowing derivatives to exist at every point in their domain, which means they have no poles or singularities. Meromorphic functions are complex functions that are differentiable except at isolated points called poles, where they exhibit singularities characterized by divergent behavior. Poles are specific types of isolated singularities where a function's value tends to infinity, distinguishing meromorphic functions from holomorphic (complex differentiable) functions that have no such singularities.
Examples of Differentiable Functions
Differentiable functions include polynomials like f(x) = x^2, trigonometric functions such as f(x) = sin(x), and exponential functions like f(z) = e^z, all of which possess well-defined derivatives at every point in their domains. In contrast, meromorphic functions, like the complex function f(z) = 1/(z - a), are differentiable except at isolated poles where they have singularities. Understanding differentiable functions is crucial for calculus and complex analysis, as they form the foundation for studying smooth behavior and complex function properties.
Examples of Meromorphic Functions
Meromorphic functions are complex functions that are holomorphic except at isolated poles, with examples including the reciprocal function f(z) = 1/z and the complex tangent function tan(z). These functions differ from generally differentiable functions by allowing singularities where they become unbounded, such as simple poles at points like z=0 for 1/z. Other notable examples include the Riemann zeta function z(s) with a meromorphic continuation exhibiting a simple pole at s=1.
Applications in Complex Analysis
Differentiable functions in complex analysis, specifically holomorphic functions, are extensively applied in conformal mapping and fluid dynamics due to their complex differentiability and preservation of angles. Meromorphic functions, characterized by isolated poles, play a critical role in residue theory and contour integration, facilitating the evaluation of complex integrals and the study of singularities in analytic functions. Both function types underpin fundamental techniques in solving boundary value problems and extending analytic continuations within complex domains.
Implications for Mathematical Modelling
Differentiable functions possess smoothness that enables precise predictions and stability in mathematical modeling, crucial for solving differential equations and representing continuous systems. Meromorphic functions, characterized by isolated poles, offer powerful tools in complex analysis for modeling phenomena with singularities or abrupt changes, such as fluid dynamics or electromagnetic fields. Understanding the distinctions between differentiable and meromorphic functions enhances the accuracy of models in physics and engineering by appropriately capturing system behaviors around regular points and singularities.
Summary Table: Differentiable vs Meromorphic
Differentiable functions are smooth and have derivatives at every point within their domain, typically defined on open subsets of the real or complex plane, while meromorphic functions are complex functions that are holomorphic except for isolated poles. The summary table highlights that differentiable functions exhibit continuous derivatives and no singularities, whereas meromorphic functions allow for isolated singularities characterized by poles of finite order. Differentiable functions are fundamental in real analysis and calculus, whereas meromorphic functions play a crucial role in complex analysis and are essential for understanding analytic continuation and residue theory.
Differentiable Infographic
 libterm.com
libterm.com