Countable nouns are words that represent items or concepts you can quantify individually, such as "apple," "book," or "idea." They can be used in singular or plural forms and work with numbers and articles like "a" or "many." Discover more about how countable nouns function and enhance your language skills by exploring the rest of this article.
Table of Comparison
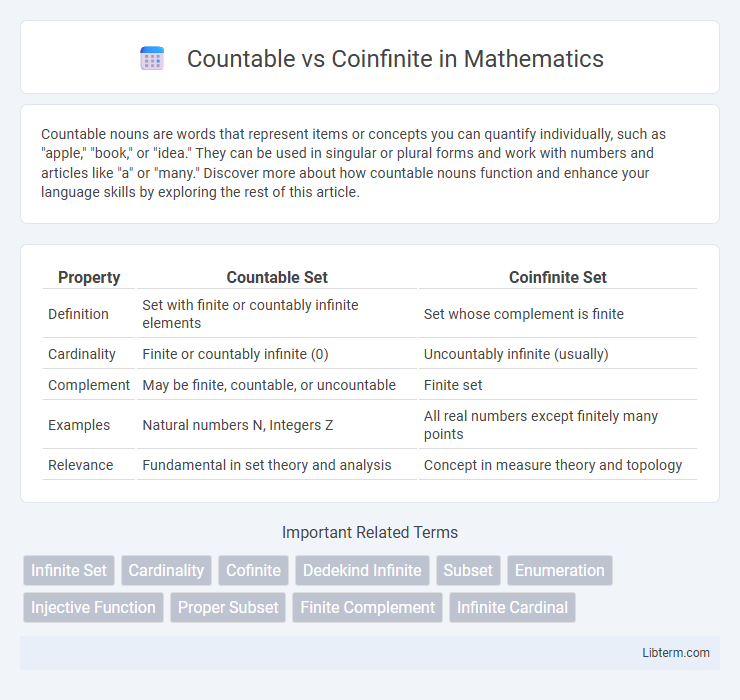
| Property | Countable Set | Coinfinite Set |
|---|---|---|
| Definition | Set with finite or countably infinite elements | Set whose complement is finite |
| Cardinality | Finite or countably infinite (0) | Uncountably infinite (usually) |
| Complement | May be finite, countable, or uncountable | Finite set |
| Examples | Natural numbers N, Integers Z | All real numbers except finitely many points |
| Relevance | Fundamental in set theory and analysis | Concept in measure theory and topology |
Introduction to Countable and Coinfinite Sets
Countable sets are those whose elements can be listed in a sequence corresponding to natural numbers, including finite sets and countably infinite sets like the integers. Coinfinite sets are subsets whose complements in a given universal set are finite, meaning almost all elements are included except for a finite number. Understanding the distinction between countable and coinfinite sets is crucial in fields like set theory and mathematical analysis, as it impacts the classification of infinities and cardinalities.
Defining Countable Sets
Countable sets are defined as those with elements that can be put into a one-to-one correspondence with the natural numbers, meaning they have the same cardinality as N or are finite. Examples include the set of integers Z and the set of rational numbers Q, both of which are countably infinite despite their density. In contrast, co-infinite sets are subsets of infinite sets whose complements are infinite, but this concept does not determine countability directly.
Understanding Coinfinite Sets
Coinfinite sets refer to subsets of an infinite set whose complements are countable, meaning the original set contains all but a countable number of elements. Unlike countable sets, which can be put into one-to-one correspondence with natural numbers, coinfinite sets are often uncountable and possess complements that are simpler or smaller in cardinality. Understanding coinfinite sets is crucial in set theory, especially when exploring properties of infinite subsets and their cardinal relationships.
Key Differences: Countable vs Coinfinite
Countable sets have elements that can be listed or enumerated one-by-one, such as natural numbers or integers, while coinfinite sets are those whose complements in a given universal set are infinite. The key difference lies in their cardinality properties; countable sets can be finite or countably infinite, whereas coinfinite sets always have an infinite complement, making them particularly relevant in fields like topology and set theory. Understanding this distinction aids in classifying sets based on their size and structural relationships within a universal context.
Examples of Countable Sets
Natural numbers, integers, and rational numbers exemplify countable sets as each element can be paired with a unique natural number. The set of even numbers or prime numbers is also countable since their elements form infinite sequences indexed by natural numbers. Countable sets contrast with uncountable sets like real numbers, which cannot be enumerated by natural numbers due to their greater cardinality.
Examples of Coinfinite Sets
Coinfinite sets are infinite sets whose complements are finite, such as the set of all natural numbers except for a finite subset like {1, 2, 3}. Another example includes the set of integers excluding a finite number of elements, for instance, Z \ {0, 1, -1}. These examples highlight how coinfinite sets maintain infiniteness while only finitely restricting elements from a larger countably infinite set.
Mathematical Properties of Countable Sets
Countable sets, characterized by their elements being put into a one-to-one correspondence with the natural numbers, exhibit a fundamental property: they are either finite or countably infinite, allowing for enumeration without omission. The mathematical properties of countable sets include closure under union and intersection, meaning the union or intersection of two countable sets remains countable. Additionally, countable sets contrast with coinfinite sets, which have infinite complements within a given infinite set, highlighting the nuanced hierarchy between different types of infinite cardinalities in set theory.
Properties and Significance of Coinfinite Sets
Coinfinite sets, whose complements in a given universal set are countable, exhibit unique properties such as being uncountably infinite and dense in many contexts. These sets are significant in measure theory and topology because they represent large subsets that maintain essential structural characteristics despite missing only a countable portion of elements. Their properties enable the study of almost everywhere behavior and genericity in mathematical analysis and probability theory.
Applications in Set Theory and Mathematics
Countable sets, including finite or countably infinite sets like the natural numbers, are fundamental in set theory for establishing concepts such as cardinality, bijections, and enumerability, facilitating the classification of infinite sets. Coinfinite sets, defined as complements of finite subsets within infinite sets, play a critical role in topological and measure-theoretic contexts by highlighting properties of largeness and density within infinite universes. Applications in mathematics leverage these distinctions to analyze convergence, continuity, and the structure of infinite groups, enabling deeper insights into both discrete and continuous mathematical systems.
Summary: Importance in Mathematical Foundations
Countable and co-infinite sets play a crucial role in mathematical foundations by characterizing the size and structure of infinite collections. Countable sets, which can be put into one-to-one correspondence with natural numbers, provide a framework for understanding enumerable infinities, essential in fields like number theory and computability. Co-infinite sets, whose complements are infinite, help in analyzing the properties of infinite subsets within larger infinite sets, supporting the study of set theory and infinite cardinalities.
Countable Infographic
 libterm.com
libterm.com