The wreath product is a fundamental construction in group theory that combines two groups in a way that captures both their individual structures and their interactions. It plays a crucial role in understanding symmetries, permutation groups, and complex algebraic systems. Explore the rest of the article to uncover how the wreath product can enhance your grasp of advanced mathematical concepts.
Table of Comparison
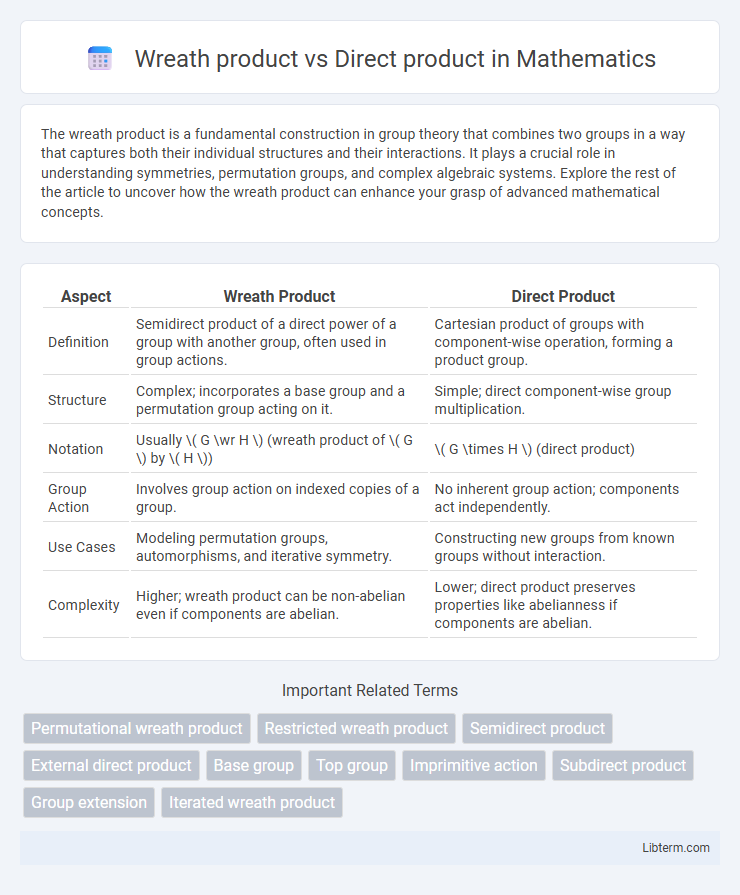
| Aspect | Wreath Product | Direct Product |
|---|---|---|
| Definition | Semidirect product of a direct power of a group with another group, often used in group actions. | Cartesian product of groups with component-wise operation, forming a product group. |
| Structure | Complex; incorporates a base group and a permutation group acting on it. | Simple; direct component-wise group multiplication. |
| Notation | Usually \( G \wr H \) (wreath product of \( G \) by \( H \)) | \( G \times H \) (direct product) |
| Group Action | Involves group action on indexed copies of a group. | No inherent group action; components act independently. |
| Use Cases | Modeling permutation groups, automorphisms, and iterative symmetry. | Constructing new groups from known groups without interaction. |
| Complexity | Higher; wreath product can be non-abelian even if components are abelian. | Lower; direct product preserves properties like abelianness if components are abelian. |
Introduction to Group Products
Group products are fundamental constructions in group theory, combining groups into larger structures while preserving group properties. The direct product forms a group by pairing elements from two groups with component-wise operation, resulting in a group where each factor operates independently. The wreath product extends this concept by incorporating a permutation action on one group component, creating a more complex semidirect product useful in analyzing symmetry and automorphism structures.
Defining the Direct Product of Groups
The direct product of groups G and H is defined as the set of all ordered pairs (g, h) where g G and h H, equipped with the group operation performed component-wise. Each element of the direct product group G x H combines elements from both groups, forming a new group whose structure reflects the independent operations of G and H. This construction preserves the group properties and enables the analysis of complex groups through simpler, constituent factors.
Understanding the Wreath Product
The wreath product is a specialized group construction combining two groups, where one acts on the copies of the other, enabling complex symmetry and permutation structures beyond the direct product's simple pairing. It generalizes the direct product by incorporating a semidirect product with a permutation action, making it essential in group theory for studying automorphisms and symmetry groups in combinatorics and algebra. Unlike the direct product, which forms independent pairs, the wreath product's hierarchical composition is crucial for analyzing iterated group actions and constructing large groups from smaller ones.
Structural Differences Between Wreath and Direct Products
Wreath products create a hierarchical structure by combining a base group with a permutation group acting on multiple copies of the base, leading to a semidirect product configuration that encodes both internal group actions and external symmetries. Direct products form a simpler structure by pairing groups element-wise without interaction between components, resulting in a purely Cartesian product of groups. The wreath product's complexity allows for encoding more intricate symmetry and automorphism patterns compared to the independent, parallel combination seen in direct products.
Algebraic Properties of Direct Products
Direct products in algebra combine multiple groups, rings, or modules by pairing their elements and performing operations component-wise, preserving the algebraic structure of each factor. The direct product of groups \( G \) and \( H \), denoted \( G \times H \), forms a group where the identity and inverses are respectively the pairs of the identities and inverses from each component, ensuring closure and associativity. This construction is associative, commutative (up to isomorphism), and the direct product inherits many fundamental properties such as normality of subgroups, making it a crucial tool for analyzing complex algebraic systems in terms of simpler ones.
Algebraic Properties of Wreath Products
Wreath products combine two groups, typically a base group and a top group acting on a set, yielding complex algebraic properties distinct from direct products, which simply pair groups element-wise. The wreath product's structure incorporates semidirect product characteristics where the top group acts on a direct product of copies of the base group, enabling intricate permutations and non-abelian behavior even when base groups are abelian. This results in wreath products being highly useful in the study of group actions, automorphism groups, and in constructing groups with prescribed properties such as high degrees of symmetry and complexity.
Applications in Group Theory
The wreath product finds extensive applications in constructing and analyzing permutation groups, enabling the modeling of complex symmetries in group actions and automorphisms. In contrast, the direct product serves as a foundational tool for decomposing groups into simpler components, facilitating the classification and study of finite groups through their factor groups. Both products play crucial roles in understanding group extensions, but the wreath product is particularly powerful in hierarchical group structures and iterative constructions.
Examples Illustrating Both Products
The wreath product of two groups, such as the symmetric group \(S_3\) wreath product with \(S_2\), yields a more complex structure combining permutation actions with a semidirect product, often used in automorphism groups of rooted trees. In contrast, the direct product of groups like \(\mathbb{Z}_2 \times \mathbb{Z}_3\) forms a straightforward Cartesian product of elements with independent group operations. Examples highlight how wreath products encode hierarchical symmetry, while direct products describe independent component-wise group operations.
Advantages and Limitations of Each Product
The wreath product offers greater flexibility in constructing complex group actions, making it advantageous for modeling hierarchical and iterative symmetries, while the direct product excels in simplicity and ease of analysis by combining groups independently. However, the wreath product can lead to significantly increased computational complexity and less intuitive structural understanding compared to the direct product, which is often limited by its inability to capture interactions between component groups. Choosing between these products depends on the desired balance between expressive power and analytical tractability in algebraic and combinatorial applications.
Summary: Choosing Between Wreath and Direct Products
Choosing between wreath and direct products depends on the desired level of complexity and group action structure; wreath products allow for a hierarchical combination of groups with more intricate permutation actions, making them suitable for constructing semi-direct product extensions. Direct products form simpler, component-wise combinations where each subgroup acts independently, ideal for straightforward group compositions without intertwining actions. Evaluating the intended application, such as symmetry modeling or group extension, guides the selection of the appropriate product type.
Wreath product Infographic
 libterm.com
libterm.com