Superalgebra generalizes algebraic structures by incorporating a grading that distinguishes even and odd elements, which plays a crucial role in mathematical physics and representation theory. This framework enables the study of symmetries extending traditional Lie algebras, with applications ranging from quantum mechanics to string theory. Discover how superalgebra influences various scientific domains as you explore the rest of this article.
Table of Comparison
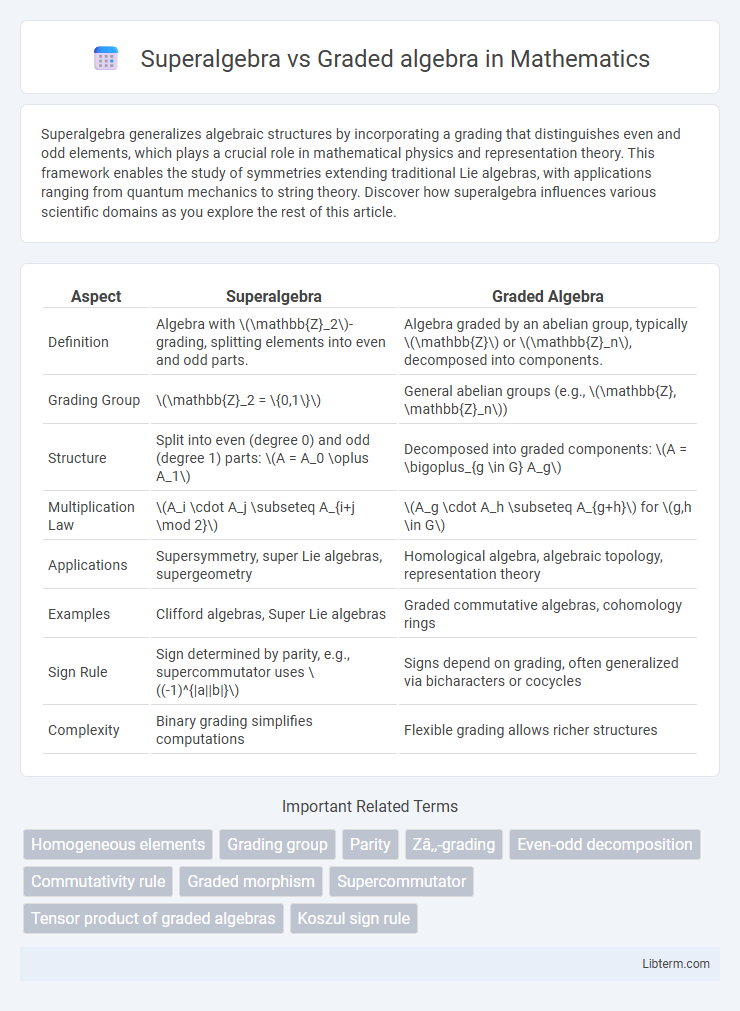
| Aspect | Superalgebra | Graded Algebra |
|---|---|---|
| Definition | Algebra with \(\mathbb{Z}_2\)-grading, splitting elements into even and odd parts. | Algebra graded by an abelian group, typically \(\mathbb{Z}\) or \(\mathbb{Z}_n\), decomposed into components. |
| Grading Group | \(\mathbb{Z}_2 = \{0,1\}\) | General abelian groups (e.g., \(\mathbb{Z}, \mathbb{Z}_n\)) |
| Structure | Split into even (degree 0) and odd (degree 1) parts: \(A = A_0 \oplus A_1\) | Decomposed into graded components: \(A = \bigoplus_{g \in G} A_g\) |
| Multiplication Law | \(A_i \cdot A_j \subseteq A_{i+j \mod 2}\) | \(A_g \cdot A_h \subseteq A_{g+h}\) for \(g,h \in G\) |
| Applications | Supersymmetry, super Lie algebras, supergeometry | Homological algebra, algebraic topology, representation theory |
| Examples | Clifford algebras, Super Lie algebras | Graded commutative algebras, cohomology rings |
| Sign Rule | Sign determined by parity, e.g., supercommutator uses \((-1)^{|a||b|}\) | Signs depend on grading, often generalized via bicharacters or cocycles |
| Complexity | Binary grading simplifies computations | Flexible grading allows richer structures |
Introduction to Superalgebra and Graded Algebra
Superalgebras generalize traditional algebras by incorporating a Z2-grading that partitions elements into even and odd components, enabling the study of symmetry in physics and mathematics. Graded algebras extend this concept through a more general grading by an abelian group, often the integers, which structures elements according to degrees and supports advanced algebraic operations in homological algebra and representation theory. The distinction lies in superalgebras' binary grading versus the multi-layered hierarchy found in graded algebras, both foundational for exploring algebraic structures with symmetry and grading properties.
Defining Superalgebra: Key Concepts
Superalgebra is an algebraic structure equipped with a Z2-grading that splits its elements into even and odd parts, enabling the study of symmetries in mathematical physics and supergeometry. Unlike general graded algebras, superalgebras specifically emphasize parity considerations, where multiplication respects the grading with sign rules dictated by the parity of elements. Key concepts include the decomposition into homogeneous components, compatibility of multiplication with grading, and the presence of supercommutation reflecting the underlying Z2-graded structure.
Understanding Graded Algebra: Basic Structure
Graded algebra is an algebraic structure decomposed into a direct sum of subspaces indexed by a grading set, often the integers, where the product of elements respects the grading by summing indices. This structure allows for the study of elements according to their degree, enabling the analysis of algebraic properties within each homogeneous component. Unlike superalgebras, which have a \(\mathbb{Z}_2\)-grading distinguishing even and odd parts, graded algebras generalize this concept using more complex grading groups.
Core Differences Between Superalgebra and Graded Algebra
Superalgebras are a specific type of graded algebra with a \(\mathbb{Z}_2\)-grading, distinguishing elements as either "even" or "odd," whereas graded algebras use a more general grading by any abelian group, often \(\mathbb{Z}\). The key difference lies in the commutation rules: superalgebras employ graded commutativity based on the parity of elements, resulting in sign changes when swapping odd elements, while graded algebras may follow more complex grading-dependent commutation relations. In applications, superalgebras underpin supersymmetry in physics through their binary grading, whereas graded algebras accommodate broader algebraic structures like homology and cohomology theories.
Grading Types: Z₂ vs General Gradings
Superalgebras are specifically graded by the cyclic group Z2, dividing elements into even and odd components that dictate sign rules in multiplication, crucial for applications in supersymmetry and theoretical physics. Graded algebras extend this concept with more general gradings over arbitrary abelian groups, enabling a richer structure and broader classification beyond the binary distinction of superalgebras. The choice of grading type impacts algebraic properties, representation theory, and cohomology theories, with Z2-gradings emphasizing parity and general gradings allowing multi-dimensional gradations for complex algebraic systems.
Algebraic Operations in Superalgebra
Superalgebra extends graded algebra by incorporating a \(\mathbb{Z}_2\)-grading that partitions elements into even and odd components, influencing algebraic operations through the sign rule in multiplication. The product of two homogeneous elements \(a\) and \(b\) in a superalgebra satisfies \(ab = (-1)^{|a||b|} ba\), where \(|a|\) and \(|b|\) denote their respective parities. This alters the commutation relations, enabling the definition of supercommutators and superderivations that are fundamental in supersymmetric algebraic structures.
Homogeneous Elements in Graded Algebras
Homogeneous elements in graded algebras are elements that belong entirely to a single grade or degree within the algebra's decomposition, often indexed by integers or elements of a grading group. In superalgebras, which are a special case of graded algebras with a grading by Z2, homogeneous elements are classified as either even or odd, corresponding to the two distinct components in the grading. Understanding the behavior and properties of these homogeneous elements is fundamental for studying the algebraic structures, representations, and module theory in both superalgebras and general graded algebras.
Applications of Superalgebra in Mathematics and Physics
Superalgebras extend graded algebras by incorporating a Z_2-grading that distinguishes even and odd elements, playing a crucial role in supersymmetry and quantum field theory. They are fundamental in the study of supergeometry, supermanifolds, and Lie superalgebras, facilitating the mathematical framework for fermionic variables and supercharges. Applications in mathematics include representation theory and category theory, while in physics, superalgebras underpin models of particle interactions and the unification of forces through supersymmetric algebraic structures.
Applications of Graded Algebras in Different Fields
Graded algebras play a crucial role in diverse fields such as algebraic topology, where their graded structures facilitate the study of cohomology rings, and in theoretical physics, particularly in supersymmetry and quantum field theory, by organizing operators according to degree or parity. In cryptography, graded algebras underpin the construction of error-correcting codes and secure communication protocols through their inherent hierarchical structure. Their applications extend to representation theory and algebraic geometry by enabling the classification of modules and sheaves via grading, enhancing the understanding of complex algebraic varieties.
Choosing Between Superalgebra and Graded Algebra: When and Why
Choosing between superalgebra and graded algebra depends primarily on the grading structure and symmetry requirements; superalgebras utilize a \(\mathbb{Z}_2\)-grading crucial for modeling fermionic and bosonic elements in supersymmetry, while graded algebras allow more general gradings like \(\mathbb{Z}\) or \(\mathbb{Z}_n\) that suit broader algebraic and topological applications. In theoretical physics, especially in supergeometry and supersymmetry, superalgebras are preferred for their inherent parity and sign rule properties, enabling consistent manipulation of even and odd elements. Conversely, graded algebras find extensive use in homological algebra and representation theory where multi-degree structures provide richer invariants and finer algebraic distinctions beyond the binary grading of superalgebras.
Superalgebra Infographic
 libterm.com
libterm.com