Singular cohomology is a fundamental tool in algebraic topology that assigns algebraic invariants to topological spaces, capturing their essential structure. It provides a way to classify spaces based on the behavior of continuous maps from standard simplices, allowing computation of topological properties like holes and connectivity. Discover how understanding singular cohomology can enhance your grasp of topological spaces in the rest of this article.
Table of Comparison
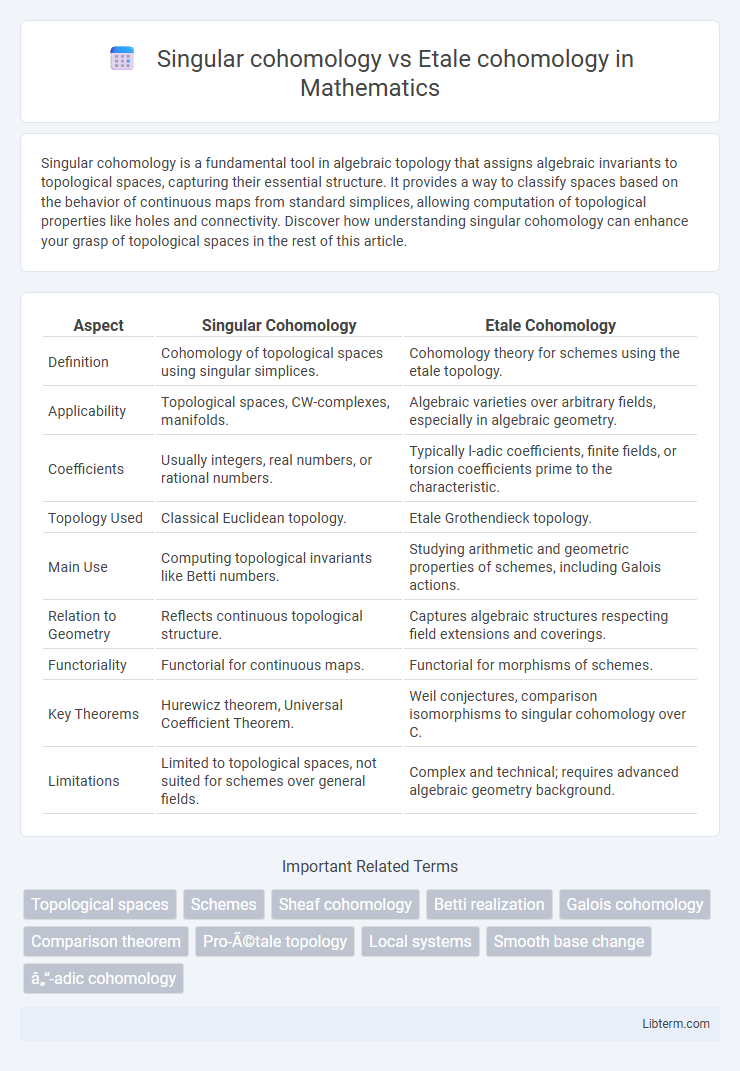
| Aspect | Singular Cohomology | Etale Cohomology |
|---|---|---|
| Definition | Cohomology of topological spaces using singular simplices. | Cohomology theory for schemes using the etale topology. |
| Applicability | Topological spaces, CW-complexes, manifolds. | Algebraic varieties over arbitrary fields, especially in algebraic geometry. |
| Coefficients | Usually integers, real numbers, or rational numbers. | Typically l-adic coefficients, finite fields, or torsion coefficients prime to the characteristic. |
| Topology Used | Classical Euclidean topology. | Etale Grothendieck topology. |
| Main Use | Computing topological invariants like Betti numbers. | Studying arithmetic and geometric properties of schemes, including Galois actions. |
| Relation to Geometry | Reflects continuous topological structure. | Captures algebraic structures respecting field extensions and coverings. |
| Functoriality | Functorial for continuous maps. | Functorial for morphisms of schemes. |
| Key Theorems | Hurewicz theorem, Universal Coefficient Theorem. | Weil conjectures, comparison isomorphisms to singular cohomology over C. |
| Limitations | Limited to topological spaces, not suited for schemes over general fields. | Complex and technical; requires advanced algebraic geometry background. |
Introduction to Cohomology Theories
Singular cohomology provides a topological invariant for spaces by associating algebraic structures to continuous mappings, capturing the global shape and connectivity of topological spaces. Etale cohomology extends these ideas to algebraic varieties over arbitrary fields by employing the etale topology, enabling the study of arithmetic and geometric properties inaccessible through classical topological methods. Both cohomology theories serve as fundamental tools in algebraic topology and algebraic geometry, facilitating the classification and analysis of spaces through their sheaf-theoretic and homological structures.
What is Singular Cohomology?
Singular cohomology is a topological invariant that assigns graded abelian groups or vector spaces to topological spaces, capturing their global shape and structure through continuous mappings from standard simplices. It is defined using singular simplices--continuous maps from the standard n-simplex into the space--and has well-established computational tools like Mayer-Vietoris sequences and cup products. Singular cohomology is widely used in algebraic topology to study spaces over the complex numbers but encounters limitations in algebraic geometry, where etale cohomology provides a more suitable framework for schemes over arbitrary fields.
What is Étale Cohomology?
Etale cohomology is a mathematical tool used to study algebraic varieties over arbitrary fields by employing the etale topology, which allows one to define sheaves and cohomology groups analogously to classical topology but in an algebraic setting. Unlike singular cohomology, which applies to topological spaces and uses continuous maps, etale cohomology captures arithmetic and geometric information of schemes over non-algebraically closed fields, often providing insight into number theory and arithmetic geometry. Developed by Grothendieck, etale cohomology facilitates the proof of the Weil conjectures and offers a way to define invariants like the etale fundamental group that do not arise in classical singular cohomology.
Key Differences: Topology vs. Algebraic Geometry
Singular cohomology is fundamentally rooted in algebraic topology, utilizing continuous maps and simplicial complexes to study the topological properties of spaces, whereas etale cohomology arises from algebraic geometry and employs the etale topology to analyze schemes with a focus on algebraic structures. Singular cohomology applies primarily to topological spaces and uses simplices to build cochains, while etale cohomology is designed for schemes over fields, capturing arithmetic and geometric information invisible to classical topologies. The key difference lies in their respective frameworks: singular cohomology handles classical topological invariants, while etale cohomology generalizes these notions to algebraic varieties via an etale site that accommodates field extensions and Galois actions.
Fundamental Group and Covering Spaces
Singular cohomology classifies topological spaces using continuous maps from simplices, directly relating to the fundamental group via covering space theory in classical topology. Etale cohomology generalizes this framework to schemes, employing etale coverings that correspond to the algebraic fundamental group, capturing arithmetic information inaccessible to singular cohomology. The etale fundamental group mirrors the profinite completion of the topological fundamental group, enabling classification of Galois covers analogous to topological covering spaces.
Coefficients and Their Significance
Singular cohomology typically uses coefficients in abelian groups or fields like Z, Q, or R, enabling direct computations of topological invariants for complex or real manifolds. In contrast, etale cohomology employs coefficients in torsion sheaves such as l-adic sheaves or finite cyclic groups, which are crucial for capturing arithmetic and geometric information in algebraic varieties over fields with nontrivial Galois actions. The choice of coefficients in etale cohomology profoundly influences its ability to detect phenomena like the action of the Galois group on etale covers, yielding deep insights into number theory and algebraic geometry.
Comparison: Applications in Algebraic Topology
Singular cohomology provides topological invariants for continuous mappings of topological spaces, enabling classification of manifolds and calculation of Betti numbers. Etale cohomology extends these invariants to schemes over arbitrary fields, crucial for studying algebraic varieties in arithmetic geometry and proving the Weil conjectures. While singular cohomology excels in classical algebraic topology over complex numbers, etale cohomology enables parallel insights in non-Archimedean and finite field settings, bridging topology and arithmetic geometry.
Comparison: Applications in Algebraic Geometry
Singular cohomology, defined using continuous maps and topological spaces, provides powerful invariants for complex algebraic varieties and their underlying analytic spaces. Etale cohomology, constructed via the etale topology on schemes, extends these invariants to varieties over arbitrary fields, including those with positive characteristic, enabling the study of arithmetic and Galois actions. This makes etale cohomology essential for proving deep results like the Weil conjectures, while singular cohomology remains fundamental for topological and differential geometric properties of complex algebraic varieties.
Limitations and Strengths of Each Theory
Singular cohomology excels in topological settings with coefficients in abelian groups, offering intuitive geometric insights and compatibility with continuous mappings but is limited to complex or real points and fails over fields lacking an analytic topology. Etale cohomology overcomes these constraints by providing a robust tool for arithmetic and algebraic varieties, handling torsion phenomena and yielding Galois representations, yet it is more abstract, technically demanding, and less intuitive due to its reliance on the etale topology and sheaf-theoretic frameworks. Both theories complement each other, with singular cohomology dominating classical topology and etale cohomology essential for addressing problems in algebraic geometry and number theory.
Bridging the Gap: When to Use Which Cohomology
Singular cohomology excels in topological settings, providing computable invariants for continuous spaces over complex numbers, while etale cohomology handles algebraic varieties over arbitrary fields, capturing arithmetic and geometric information missed by singular methods. Use singular cohomology for classical topological problems involving manifolds or CW complexes, and choose etale cohomology when dealing with arithmetic schemes, especially in positive characteristic or non-algebraically closed fields. Bridging these theories involves comparing their outputs via comparison theorems over complex varieties, leveraging singular cohomology's topological intuition alongside etale cohomology's arithmetic power.
Singular cohomology Infographic
 libterm.com
libterm.com