A Cartesian category is a mathematical structure in category theory characterized by the existence of finite products, including a terminal object, which facilitate the representation of product types and pairing operations. It provides a framework for modeling computations and functional programming concepts by enabling the manipulation of objects and morphisms with product-like behavior. Explore the rest of the article to deepen your understanding of Cartesian categories and their applications in theoretical computer science.
Table of Comparison
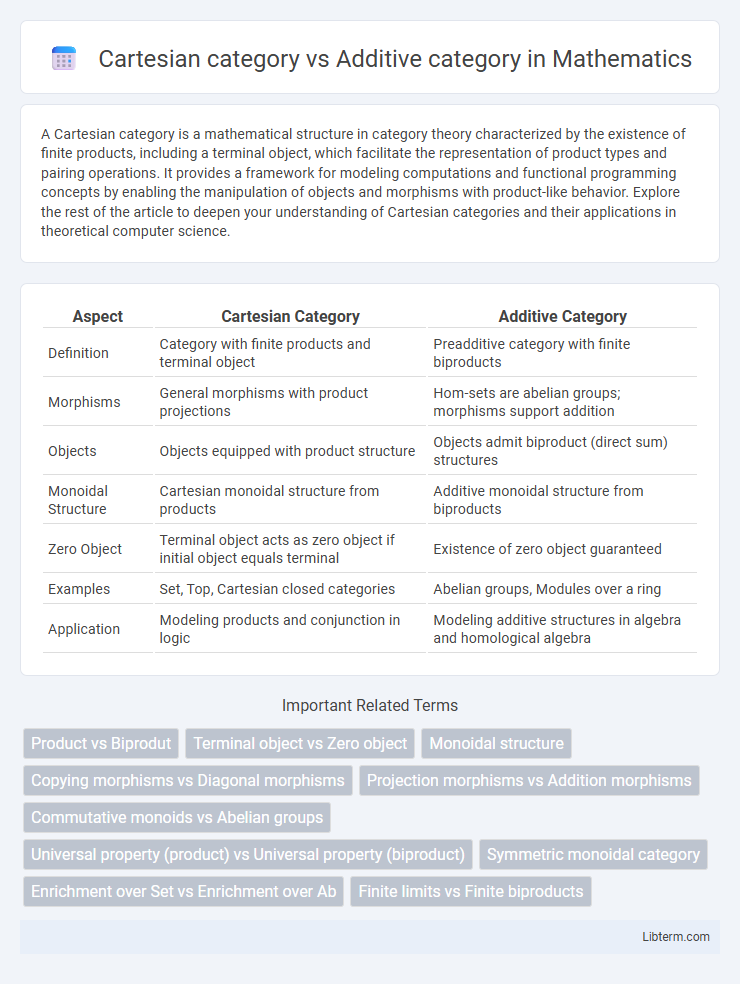
| Aspect | Cartesian Category | Additive Category |
|---|---|---|
| Definition | Category with finite products and terminal object | Preadditive category with finite biproducts |
| Morphisms | General morphisms with product projections | Hom-sets are abelian groups; morphisms support addition |
| Objects | Objects equipped with product structure | Objects admit biproduct (direct sum) structures |
| Monoidal Structure | Cartesian monoidal structure from products | Additive monoidal structure from biproducts |
| Zero Object | Terminal object acts as zero object if initial object equals terminal | Existence of zero object guaranteed |
| Examples | Set, Top, Cartesian closed categories | Abelian groups, Modules over a ring |
| Application | Modeling products and conjunction in logic | Modeling additive structures in algebra and homological algebra |
Introduction to Cartesian and Additive Categories
Cartesian categories feature finite products enabling the definition of product objects and projection morphisms, facilitating the modeling of conjunctions in logic and tuples in programming. Additive categories possess biproducts, combining both product and coproduct structures, allowing for addition of morphisms and enriching the category with an abelian group structure on hom-sets. The distinction lies in Cartesian categories emphasizing product objects suitable for product-type constructions, while additive categories support algebraic operations essential in homological algebra and representation theory.
Defining Cartesian Categories
Cartesian categories are defined by the presence of finite products, including a terminal object and binary product objects that satisfy universal property conditions for projections and pairing. They enable modeling of product types and support the construction of morphisms that factor uniquely through these product objects, reflecting a categorical abstraction of cartesian products in set theory. Additive categories, in contrast, emphasize biproducts with zero morphisms and abelian group structures on hom-sets, diverging from the purely product-oriented framework of Cartesian categories.
Core Properties of Cartesian Categories
Cartesian categories are characterized by the existence of finite products, including a terminal object and binary products that satisfy universal properties. These categories support diagonal morphisms and projections, enabling copying and deletion operations that structure morphisms like conjunction in logic. In contrast, additive categories are enriched over abelian groups, featuring biproducts where products and coproducts coincide, lacking the universal property of Cartesian products essential to Cartesian categories.
Understanding Additive Categories
Additive categories are enriched over abelian groups, meaning their hom-sets are abelian groups and composition is bilinear, distinguishing them from Cartesian categories, which are defined by finite products. In additive categories, the presence of zero objects, biproducts (which serve as both products and coproducts), and kernels enables a richer algebraic structure conducive to homological algebra. Understanding additive categories is crucial for studying module categories and abelian categories, where morphisms exhibit additive properties absent in purely Cartesian settings.
Essential Characteristics of Additive Categories
Additive categories are characterized by the presence of finite biproducts, where products and coproducts coincide, enabling direct sum decompositions of objects. Morphism sets in additive categories form abelian groups, allowing for well-defined addition and zero morphisms that satisfy compatibility conditions. Unlike Cartesian categories, which focus on product structures and terminal objects, additive categories emphasize linear structures essential for homological algebra and module theory.
Structural Differences Between Cartesian and Additive Categories
Cartesian categories feature finite products with terminal objects and diagonal morphisms enabling duplication, emphasizing product-like structures and projections. Additive categories possess biproducts combining product and coproduct aspects, allowing direct sums and zero morphisms, which support additive structure on hom-sets. The core structural difference lies in Cartesian categories prioritizing product-based operations and duplication, while additive categories integrate additive behaviors with enriched hom-sets and biproduct decompositions.
Morphisms in Cartesian vs Additive Contexts
Morphisms in Cartesian categories represent functions that preserve product structures, characterized by projections and pairing operations that maintain universal properties of products. In Additive categories, morphisms form abelian groups with addition and zero morphisms, enabling biproducts where both product and coproduct structures coexist and morphisms are additive homomorphisms. The distinction lies in Cartesian morphisms emphasizing structural preservation of products, while Additive morphisms incorporate algebraic addition, making the category enriched over abelian groups.
Examples Illustrating Cartesian and Additive Categories
Cartesian categories include examples such as the category of sets with product as the categorical product and singleton set as the terminal object, reflecting the universal property of products and projections. Additive categories are exemplified by the category of abelian groups where hom-sets are abelian groups, and the biproduct simultaneously serves as product and coproduct, demonstrating additive structure in morphisms. In contrast, while Cartesian categories emphasize products and terminal objects, additive categories highlight biproducts and the enrichment over abelian groups for morphism sets.
Applications and Relevance in Category Theory
Cartesian categories model product types and support finite limits, enabling applications in typed lambda calculus and functional programming semantics, where they represent conjunctions and pairing constructs. Additive categories generalize abelian group structures on hom-sets, crucial in homological algebra and representation theory, allowing direct sum decompositions and kernel-cokernel analysis. Both frameworks enhance categorical foundations: Cartesian categories facilitate logical and computational interpretations, while additive categories underpin algebraic and topological invariants.
Summary: Comparing Cartesian and Additive Categories
Cartesian categories emphasize finite products and terminal objects, enabling the modeling of product types and pairing operations in category theory. Additive categories focus on biproducts and enriched hom-sets over abelian groups, facilitating the direct sum of objects and morphism addition. Understanding their structural differences highlights Cartesian categories' role in product-related constructions compared to Additive categories' support for additive and linear structures.
Cartesian category Infographic
 libterm.com
libterm.com