Trivial matters often seem insignificant but can impact your overall productivity and focus more than expected. Minimizing distractions by addressing these small issues helps create a clearer path to achieving your goals. Explore the rest of the article to discover practical strategies for managing trivial challenges effectively.
Table of Comparison
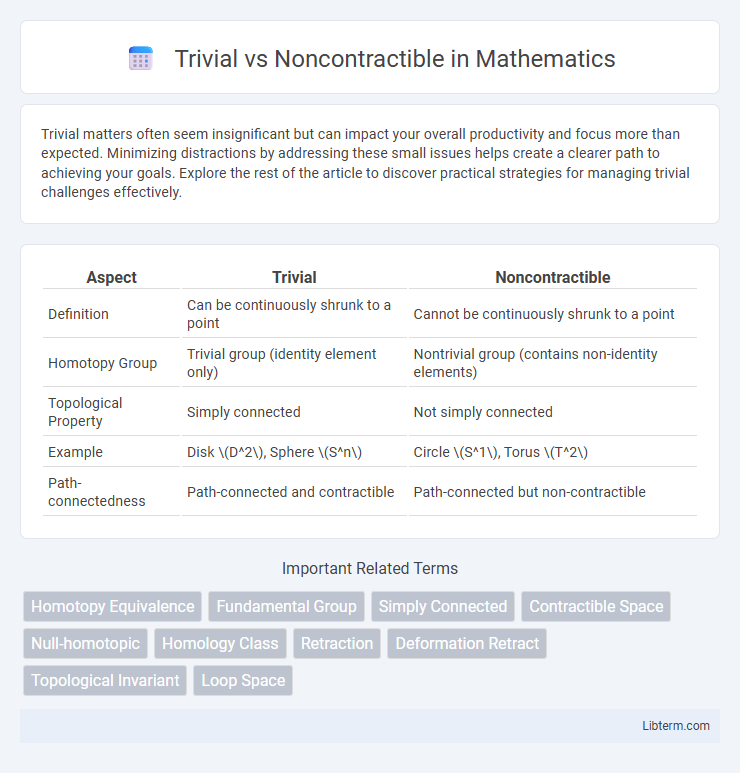
| Aspect | Trivial | Noncontractible |
|---|---|---|
| Definition | Can be continuously shrunk to a point | Cannot be continuously shrunk to a point |
| Homotopy Group | Trivial group (identity element only) | Nontrivial group (contains non-identity elements) |
| Topological Property | Simply connected | Not simply connected |
| Example | Disk \(D^2\), Sphere \(S^n\) | Circle \(S^1\), Torus \(T^2\) |
| Path-connectedness | Path-connected and contractible | Path-connected but non-contractible |
Understanding Trivial and Noncontractible Concepts
Trivial and noncontractible concepts differ fundamentally in topology and algebraic structures; trivial concepts refer to objects that can be continuously deformed to a point, indicating simple, contractible spaces with no holes. Noncontractible concepts involve spaces or loops that cannot be shrunk to a point without tearing, highlighting essential topological features such as holes or obstacles reflected in nontrivial homotopy groups. Understanding these distinctions is crucial in fields like algebraic topology, where the contractibility property informs classification and analysis of complex geometric and algebraic objects.
Key Differences Between Trivial and Noncontractible
Trivial loops are contractible loops in a topological space that can be continuously shrunk to a point, reflecting a simple, non-complex topology. Noncontractible loops cannot be reduced to a point without leaving the space, indicating the presence of holes or topological obstacles in the structure. The key difference lies in their homotopy class: trivial loops represent the identity element in the fundamental group, whereas noncontractible loops correspond to nontrivial elements, revealing essential features of the space's shape.
Mathematical Definitions of Trivial vs Noncontractible
A trivial space in topology is one that is contractible to a single point, meaning it has the same homotopy type as a point and all its higher homotopy groups are trivial. Noncontractible spaces, however, cannot be continuously shrunk to a point, often exhibiting nontrivial fundamental groups or higher homotopy groups. The distinction between trivial and noncontractible spaces is central in algebraic topology, where contractibility implies homotopy equivalence to a point and noncontractibility reveals rich topological structures.
Topological Implications of Trivial and Noncontractible
Trivial topological spaces exhibit no nontrivial loops, resulting in a simple homotopy type that is contractible to a point, making their fundamental group trivial. Noncontractible spaces contain loops that cannot be continuously shrunk to a point, leading to nontrivial fundamental groups and richer topological invariants. These differences are crucial in classifying spaces, impacting concepts such as homotopy, covering spaces, and the calculation of homology and cohomology groups.
Examples of Trivial Structures in Mathematics
Trivial structures in mathematics include the trivial group, which contains only the identity element, and the trivial vector space, consisting solely of the zero vector. The trivial ring includes a single element that acts as both the additive and multiplicative identity, while trivial topological spaces feature only the empty set and the entire space as open sets. These examples highlight the simplest, highly constrained instances in their respective mathematical categories.
Illustrative Cases of Noncontractible Spaces
Noncontractible spaces such as the circle (S1) and the torus (T2) exhibit topological features that prevent them from being continuously shrunk to a point, contrasting with trivial contractible spaces like a disk. The fundamental group of noncontractible spaces captures essential loops that cannot be contracted, exemplified by the nontrivial p1(S1) Z and p1(T2) Z x Z. Examples in algebraic topology demonstrate how these spaces serve as critical models for homotopy theory and contribute to the classification of topological spaces based on their noncontractible properties.
Significance in Algebraic Topology
Trivial and noncontractible spaces play crucial roles in algebraic topology by distinguishing between spaces that can be continuously deformed to a point and those that cannot, impacting the computation of fundamental groups and homotopy types. The significance lies in how noncontractible spaces exhibit essential topological features, such as holes or loops, which contribute to invariants like homology and cohomology groups. Understanding these properties enables the classification of spaces and the detection of topological obstructions in complex systems.
Applications in Physics and Engineering
Trivial and noncontractible spaces play crucial roles in physics and engineering, particularly in the study of topological phases of matter and electromagnetic field configurations. In condensed matter physics, noncontractible loops in topological insulators correspond to robust edge states that are immune to perturbations, enabling advancements in quantum computing and spintronics. Engineering applications utilize noncontractible topologies in the design of resilient structures and stable control systems, where trivial spaces often model simple, deformable configurations without persistent constraints.
Common Misconceptions: Trivial vs Noncontractible
The common misconception between trivial and noncontractible cycles lies in their roles within topological spaces: trivial cycles are those that can be continuously shrunk to a point without leaving the space, while noncontractible cycles cannot be contracted and represent essential holes or voids in the topology. Many confuse trivial cycles with simple loops, overlooking that contractibility depends on the space's homotopy properties, not just the cycle's shape. Recognizing this distinction is crucial for correctly analyzing fundamental groups and homology in algebraic topology.
Summary and Key Takeaways
Trivial components refer to elements in a structure that can be continuously shrunk to a point without leaving the space, indicating a lack of complexity or holes, while noncontractible components cannot be reduced in this way, highlighting essential topological features. Key takeaways include understanding that triviality implies simplicity and homotopy equivalence to a point, whereas noncontractibility signals the presence of fundamental topological obstructions or invariants. Recognizing the difference aids in classifying spaces and analyzing their geometric and topological properties effectively.
Trivial Infographic
 libterm.com
libterm.com