Poincare series are generating functions that encode the dimensions of graded components in algebraic or geometric structures, playing a crucial role in topology and complex analysis. They reveal information about the growth rates and symmetries of mathematical objects such as groups or manifolds. Discover how understanding Poincare series can deepen your insight into these fascinating areas by reading the rest of the article.
Table of Comparison
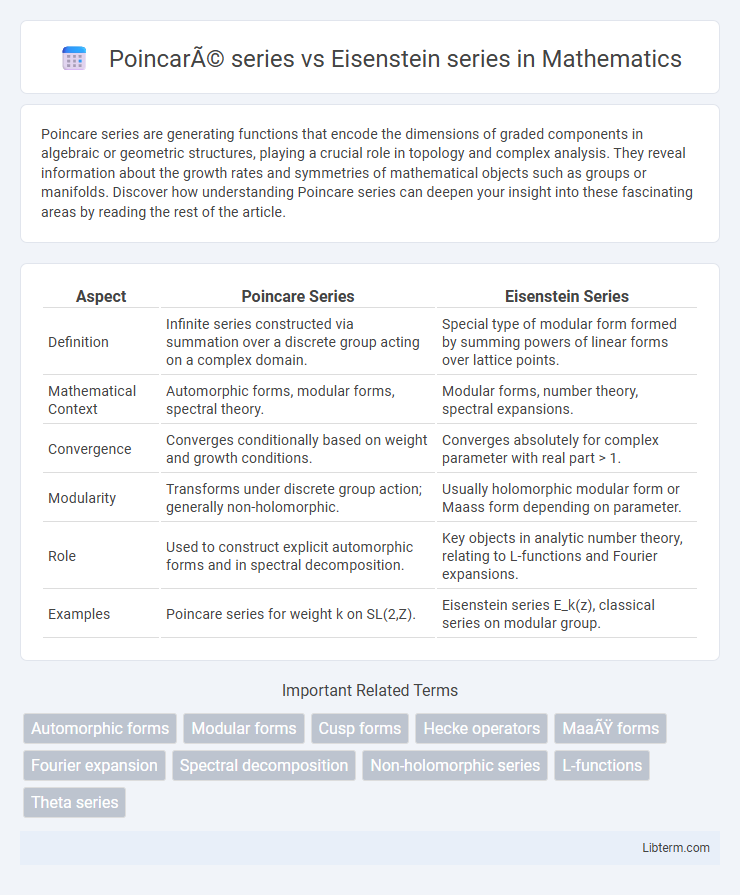
| Aspect | Poincare Series | Eisenstein Series |
|---|---|---|
| Definition | Infinite series constructed via summation over a discrete group acting on a complex domain. | Special type of modular form formed by summing powers of linear forms over lattice points. |
| Mathematical Context | Automorphic forms, modular forms, spectral theory. | Modular forms, number theory, spectral expansions. |
| Convergence | Converges conditionally based on weight and growth conditions. | Converges absolutely for complex parameter with real part > 1. |
| Modularity | Transforms under discrete group action; generally non-holomorphic. | Usually holomorphic modular form or Maass form depending on parameter. |
| Role | Used to construct explicit automorphic forms and in spectral decomposition. | Key objects in analytic number theory, relating to L-functions and Fourier expansions. |
| Examples | Poincare series for weight k on SL(2,Z). | Eisenstein series E_k(z), classical series on modular group. |
Introduction to Modular Forms
Poincare series and Eisenstein series are fundamental examples of modular forms constructed on the upper half-plane with respect to a discrete subgroup of SL(2,R). Poincare series are defined by summing a seed function over the orbit of the modular group, providing a basis for spaces of cusp forms with rapid decay at cusps. Eisenstein series, by contrast, are non-cuspidal modular forms formed as series over lattice points, exhibiting explicit Fourier expansions that encode arithmetic data such as divisor sums.
Defining the Poincaré Series
The Poincare series is defined as a sum over a discrete group, typically a Fuchsian group, acting on the upper half-plane, constructed from a seed function that is automorphic under the stabilizer subgroup. Specifically, for a given weight k and a cusp form or modular form, the Poincare series involves summing the transforms of the seed function under all group elements, ensuring modular invariance. This contrasts with Eisenstein series, which are typically defined as sums over cosets related to parabolic subgroups, emphasizing different convergence and spectral properties within the theory of automorphic forms.
Understanding the Eisenstein Series
The Eisenstein series is a fundamental example of a modular form constructed as a sum over lattice points, exhibiting important automorphic properties and meromorphic continuation. Unlike Poincare series, which are built from non-holomorphic seed functions to create new modular forms, Eisenstein series have explicit Fourier expansions that reveal deep connections with L-functions and number theory. The analytic behavior of Eisenstein series, including their constant term and residues, plays a crucial role in the spectral theory of automorphic forms and the Langlands program.
Historical Context and Development
Poincare series, introduced by Henri Poincare in the late 19th century, laid foundational work for automorphic forms by constructing series invariant under discrete groups, particularly in the setting of Fuchsian groups. Eisenstein series, developed by Gotthold Eisenstein earlier in the 19th century, originated from studies on elliptic functions and modular forms, providing explicit examples of series with modular invariance and playing a crucial role in the spectral theory of automorphic forms. Both series have evolved through contributions by mathematicians such as Selberg and Maass, profoundly influencing modern analytic number theory and representation theory.
Fourier Expansion: Poincaré vs Eisenstein
Poincare series and Eisenstein series exhibit distinct Fourier expansions reflecting their foundational structures in modular form theory. The Fourier expansion of a Poincare series typically features rapidly decaying coefficients linked to cusp forms, emphasizing their square-integrable nature on the modular surface. In contrast, Eisenstein series contain constant and non-decaying terms in their Fourier expansion, encoding data from continuous spectra and contributing to the analytic continuation of L-functions.
Analytic Properties and Convergence
Poincare series are constructed as sums over discrete groups acting on the upper half-plane, exhibiting meromorphic continuation and often converging conditionally or absolutely depending on the spectral parameter. Eisenstein series, defined through series over parabolic subgroups, possess uniform absolute convergence in certain half-planes and admit meromorphic continuation with functional equations related to automorphic L-functions. Analytic properties of both series, including their spectral expansions and location of poles, play crucial roles in modern analytic number theory and the theory of automorphic forms.
Modular Transformation Behavior
Poincare series and Eisenstein series are both fundamental in the theory of modular forms, characterized by their distinct modular transformation behaviors. Poincare series are constructed explicitly to transform like modular forms of a given weight under the action of the modular group, ensuring automorphicity with prescribed growth conditions. Eisenstein series exhibit modular invariance and serve as prototype examples of modular forms, featuring explicit Fourier expansions and playing a central role in understanding the structure of the space of modular forms through their well-defined transformation under SL(2,Z).
Applications in Number Theory
Poincare series and Eisenstein series play crucial roles in number theory, particularly in the study of modular forms and automorphic representations. Poincare series provide explicit constructions of modular forms with prescribed Fourier coefficients, enabling the analysis of L-functions and arithmetic properties of modular curves. Eisenstein series contribute to understanding the distribution of arithmetic objects, such as the behavior of prime numbers in arithmetic progressions and the spectral decomposition of automorphic forms on arithmetic groups.
Interplay and Differences between the Two Series
Poincare series and Eisenstein series both play crucial roles in the theory of modular forms, with Poincare series constructed as sums over discrete groups to generate cusp forms, while Eisenstein series arise from summing over cosets and often represent non-cuspidal modular forms. The interplay between these series is evident in the spectral decomposition of automorphic forms, where Eisenstein series contribute continuous spectrum components and Poincare series correspond to discrete spectrum elements. Their key difference lies in analytic properties: Eisenstein series possess meromorphic continuations with known poles, whereas Poincare series are tailored to produce square-integrable eigenfunctions of the Laplacian, highlighting distinctions in growth, convergence, and modular invariance.
Modern Research and Open Questions
Modern research on Poincare series and Eisenstein series explores their deep connections in automorphic forms and spectral theory, with emphasis on analytic properties and convergence in higher rank groups. Open questions include the explicit description of Fourier coefficients, the growth of Poincare series in various cuspidal settings, and the role of Eisenstein series residues in arithmetic geometry. Advances in these areas potentially impact Langlands program conjectures and the understanding of L-functions.
Poincaré series Infographic
 libterm.com
libterm.com