A register machine is a theoretical computational model used in computer science to study algorithms and complexity through a simplified set of operations on a finite number of registers. It manipulates data stored in registers using instructions like increment, decrement, and conditional jumps, offering a foundational understanding of how computers process information. Explore the rest of the article to discover how register machines influence modern computing and algorithm design.
Table of Comparison
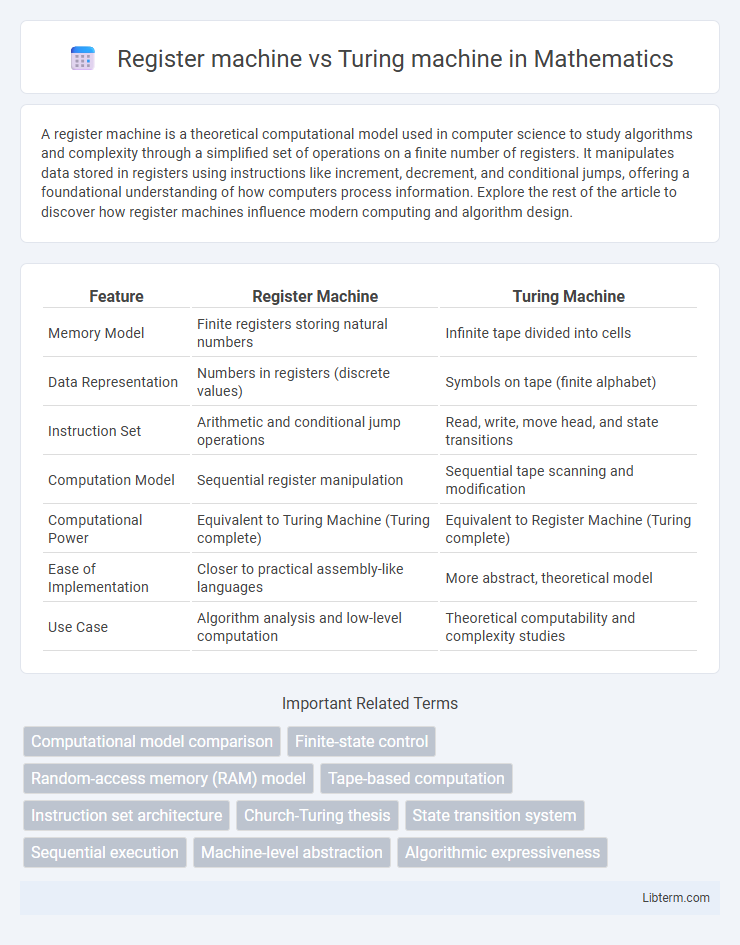
| Feature | Register Machine | Turing Machine |
|---|---|---|
| Memory Model | Finite registers storing natural numbers | Infinite tape divided into cells |
| Data Representation | Numbers in registers (discrete values) | Symbols on tape (finite alphabet) |
| Instruction Set | Arithmetic and conditional jump operations | Read, write, move head, and state transitions |
| Computation Model | Sequential register manipulation | Sequential tape scanning and modification |
| Computational Power | Equivalent to Turing Machine (Turing complete) | Equivalent to Register Machine (Turing complete) |
| Ease of Implementation | Closer to practical assembly-like languages | More abstract, theoretical model |
| Use Case | Algorithm analysis and low-level computation | Theoretical computability and complexity studies |
Introduction to Register Machines and Turing Machines
Register machines operate using a finite set of registers that store natural numbers and execute instructions such as increment, decrement, and conditional jumps, providing a practical model for algorithmic computation. Turing machines use an infinite tape divided into cells and a tape head that reads and writes symbols based on a finite set of states and transition rules, forming the foundational model of computability in theoretical computer science. Both models are equivalent in computational power, with register machines offering a more intuitive arithmetic-based approach and Turing machines emphasizing symbol manipulation.
Historical Background and Development
Register machines emerged in the mid-20th century as a simplified, more practical alternative to Turing machines, designed to model algorithms with finite resources and explicit storage through registers. Alan Turing introduced the Turing machine concept in 1936 to formalize computation and algorithmic processes, laying the foundation for modern theoretical computer science. Both models significantly influenced the development of automata theory and complexity classes, with register machines often preferred in studies of computational complexity due to their closer alignment with real-world computer architectures.
Fundamental Architecture and Components
Register machines employ a finite set of registers that store natural numbers manipulated via basic instructions like increment, decrement, and conditional jumps. Turing machines consist of an infinite tape divided into cells, a tape head for reading and writing symbols, and a finite state control dictating operations based on the current state and tape symbol. The fundamental difference lies in storage structures: register machines use discrete registers with direct access, whereas Turing machines rely on sequential tape access for memory manipulation.
Computational Models: Similarities and Differences
Register machines and Turing machines both serve as foundational computational models that capture the essence of algorithmic processes through abstract machines manipulating symbols. Register machines operate using a finite number of registers storing natural numbers and execute instructions like increment, decrement, and conditional jumps, offering a register-based computational framework. In contrast, Turing machines employ an infinite tape divided into cells with a read/write head moving bidirectionally, emphasizing a tape-based computation model; both models are computationally equivalent in terms of language recognition and function computability but differ in operational structure and representation.
Instruction Sets and Operational Mechanisms
Register machines use a finite set of instructions primarily focused on arithmetic operations, data transfer between registers, and conditional branching, enabling direct manipulation of stored values in registers. Turing machines operate with a simpler instruction set consisting of read, write, move, and state transition commands, functioning on an infinite tape where the head processes symbols sequentially. The operational mechanism of register machines emphasizes efficient register access and computation, while Turing machines rely on sequential symbol processing and state changes to perform computations.
Memory Management and Data Representation
Register machines utilize a finite set of registers for direct storage and manipulation of natural numbers, enabling efficient random access memory management. Turing machines employ an infinite tape as memory, with data represented as symbols on discrete cells, accessed sequentially, leading to slower data retrieval compared to register machines. The register machine's architecture supports explicit addressing and arithmetic operations, whereas the Turing machine relies on state transitions and symbol rewriting for data processing.
Computational Power and Universality
Register machines and Turing machines are equivalent in computational power, both capable of simulating any algorithm and recognizing recursively enumerable languages. Register machines operate on a finite number of registers storing natural numbers, making them a practical model for studying low-level computation, while Turing machines manipulate symbols on an infinite tape. Both models are universal, meaning each can simulate the other with only a polynomial time overhead, reinforcing their foundational role in computability theory.
Practical Applications and Use Cases
Register machines excel in practical applications requiring direct manipulation of numerical data and efficient execution of arithmetic operations, making them ideal for low-level programming and embedded system simulations. Turing machines serve as foundational theoretical models for computability and complexity theory, providing a universal framework for algorithm analysis and decision problem classification. The practical use of register machines in hardware design contrasts with Turing machines' role in theoretical computer science and complexity class characterization.
Theoretical Implications in Computer Science
Register machines provide a finite set of registers and instructions for arithmetic and control operations, modeling computation with a more hardware-oriented approach than Turing machines. Turing machines, defined by an infinite tape and a head for reading and writing symbols, serve as the foundational model for computability and algorithmic theory, demonstrating the limits of what is computationally possible. Comparing both models enhances understanding of computational complexity, decidability, and the Church-Turing thesis, solidifying core principles in theoretical computer science.
Comparative Advantages and Limitations
Register machines offer efficient manipulation of numeric data with direct access to registers, enabling faster arithmetic and conditional operations compared to Turing machines, which rely on sequential tape access. Turing machines provide a more abstract and universal model of computation, capable of simulating any algorithm despite slower step-by-step execution due to linear tape movements. Register machines excel in practical algorithm implementation and machine-level programming, while Turing machines serve as the foundational theoretic model for computability and complexity theory.
Register machine Infographic
 libterm.com
libterm.com