Subharmonics are frequencies that occur at fractional intervals of a fundamental frequency, playing a crucial role in fields like acoustics, signal processing, and vibration analysis. Understanding subharmonics helps you analyze complex waveforms and identify patterns that differ from standard harmonic sequences. Explore the rest of the article to deepen your knowledge of subharmonics and their practical applications.
Table of Comparison
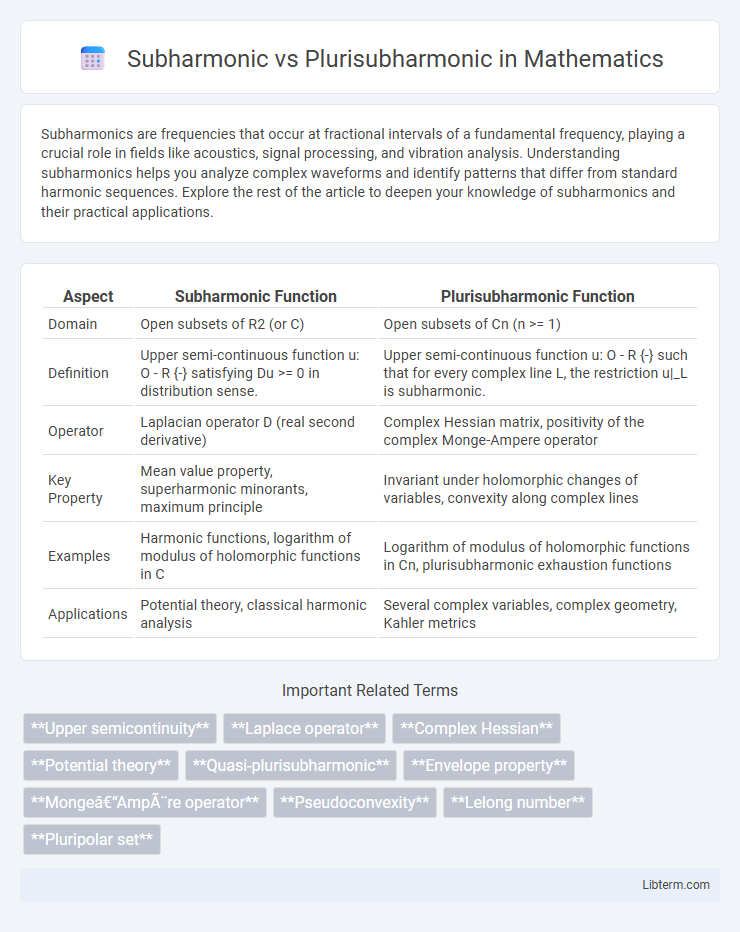
| Aspect | Subharmonic Function | Plurisubharmonic Function |
|---|---|---|
| Domain | Open subsets of R2 (or C) | Open subsets of Cn (n >= 1) |
| Definition | Upper semi-continuous function u: O - R {-} satisfying Du >= 0 in distribution sense. | Upper semi-continuous function u: O - R {-} such that for every complex line L, the restriction u|_L is subharmonic. |
| Operator | Laplacian operator D (real second derivative) | Complex Hessian matrix, positivity of the complex Monge-Ampere operator |
| Key Property | Mean value property, superharmonic minorants, maximum principle | Invariant under holomorphic changes of variables, convexity along complex lines |
| Examples | Harmonic functions, logarithm of modulus of holomorphic functions in C | Logarithm of modulus of holomorphic functions in Cn, plurisubharmonic exhaustion functions |
| Applications | Potential theory, classical harmonic analysis | Several complex variables, complex geometry, Kahler metrics |
Introduction to Subharmonic and Plurisubharmonic Functions
Subharmonic functions are upper semi-continuous functions defined on an open subset of the complex plane that satisfy the mean value property with respect to harmonic functions, playing a key role in potential theory and complex analysis. Plurisubharmonic functions generalize subharmonic functions to several complex variables, being upper semi-continuous functions whose restriction to any complex line is subharmonic, essential in the study of complex manifolds and pluripotential theory. Both function classes provide crucial tools for analyzing complex structures, with subharmonicity focusing on single-variable contexts and plurisubharmonicity extending these properties to multi-variable, higher-dimensional complex spaces.
Defining Subharmonic Functions: Key Characteristics
Subharmonic functions are upper semi-continuous functions defined on an open subset of the complex plane that satisfy the mean value property, where the value at any point is less than or equal to the average value over any surrounding circle. These functions are characterized by their submean inequality and are closely related to harmonic functions, serving as potential functions in potential theory. Unlike plurisubharmonic functions, which generalize subharmonic functions to several complex variables, subharmonic functions are strictly one-variable constructs with essential applications in complex analysis and partial differential equations.
Plurisubharmonic Functions: Concepts and Properties
Plurisubharmonic functions extend subharmonic functions to several complex variables, defined on complex domains with values in the extended real line, and characterized by their upper semi-continuity and subharmonicity when restricted to any complex line. They play a crucial role in complex analysis, especially in potential theory and complex geometry, as they are instrumental in defining pseudoconvex domains and in solving the complex Monge-Ampere equation. Key properties of plurisubharmonic functions include their invariance under holomorphic coordinate changes, the fact that the sum of plurisubharmonic functions remains plurisubharmonic, and their role as exhaustion functions in Stein manifolds.
Mathematical Foundations: Comparison of Definitions
Subharmonic functions are defined on open subsets of the complex plane and satisfy the mean value inequality with respect to harmonic functions, ensuring that their value at any point is less than or equal to the average over surrounding circles. Plurisubharmonic functions generalize this concept to several complex variables, requiring subharmonicity along every complex line in the multivariate domain, characterized by their upper semi-continuity and the positivity of the complex Hessian matrix in the sense of distributions. The key mathematical distinction lies in the domain and curvature conditions: subharmonic functions concern one complex variable with Laplacian non-negativity, while plurisubharmonic functions involve complex variables in higher dimensions with conditions expressed via the complex Hessian and the Levi form.
Core Applications in Complex Analysis
Subharmonic functions play a crucial role in potential theory and are extensively used to study the growth and boundary behavior of holomorphic functions in one complex variable. Plurisubharmonic functions generalize this concept to several complex variables, enabling the analysis of complex manifolds, the study of pseudoconvex domains, and providing essential tools for solving the Levi problem. Both function classes underpin key results in complex analysis, including the construction of Green functions and the formulation of plurisubharmonic exhaustion functions essential for understanding complex analytic and geometric structures.
Subharmonicity in Potential Theory
Subharmonicity in potential theory characterizes functions whose Laplacian is non-negative, ensuring they lie below the mean of their values on surrounding neighborhoods, making them critical for describing equilibrium potentials and harmonic measure. Unlike plurisubharmonic functions, which generalize subharmonicity to several complex variables with respect to the complex Hessian, subharmonic functions are defined on real domains and serve as fundamental tools in studying Laplace's equation and classical potential theory. Key applications of subharmonicity include constructing superharmonic barriers, solving Dirichlet problems, and analyzing properties of Green's functions in Euclidean spaces.
Plurisubharmonicity in Several Complex Variables
Plurisubharmonic functions are a fundamental tool in the theory of several complex variables, extending the concept of subharmonicity to higher dimensions by requiring that their restriction to every complex line is subharmonic. These functions naturally arise in complex analysis and geometry, playing a crucial role in the study of pseudoconvex domains, pluripotential theory, and the characterization of holomorphic convexity. The property of plurisubharmonicity is essential for understanding complex Monge-Ampere equations and constructing exhaustive plurisubharmonic functions used in complex manifolds and Stein spaces.
Similarities and Differences: Subharmonic vs Plurisubharmonic
Subharmonic functions and plurisubharmonic functions both generalize the concept of harmonicity by allowing certain controlled types of growth and are essential in potential theory and complex analysis. Subharmonic functions are defined on real or complex planes and satisfy the mean value inequality, while plurisubharmonic functions extend this concept to several complex variables, requiring subharmonicity along every complex line. The key difference lies in dimensionality and complexity: subharmonic functions operate in one complex dimension or two real dimensions, whereas plurisubharmonic functions capture multidimensional complex structures and are vital in studying pseudoconvexity and complex manifolds.
Common Misconceptions and Clarifications
Subharmonic functions are often confused with plurisubharmonic functions due to their similar names, but subharmonicity applies to real-valued functions in one variable, while plurisubharmonicity extends to complex variables with multiple dimensions. A common misconception is that all plurisubharmonic functions are simply subharmonic in each variable separately; however, plurisubharmonic functions must satisfy a joint convexity condition in several complex variables, which is a stricter and more complex criterion. Clarifying this distinction helps in understanding their roles in complex analysis, particularly in potential theory and complex geometry.
Conclusion: Importance in Modern Mathematical Analysis
Subharmonic and plurisubharmonic functions are crucial in modern mathematical analysis due to their roles in potential theory and several complex variables. Subharmonic functions generalize harmonic functions providing key insights into Laplace's equation, while plurisubharmonic functions extend these concepts to complex manifolds, essential in complex geometry and complex analysis. Their importance lies in enabling deep understanding of function behavior, singularities, and complex structures, underpinning advances in both theoretical and applied mathematics.
Subharmonic Infographic
 libterm.com
libterm.com