An equation is a mathematical statement asserting the equality of two expressions, typically containing variables and constants. It serves as a fundamental tool for solving problems across diverse fields such as physics, engineering, and economics. Explore the article to deepen your understanding of how equations can enhance your problem-solving skills.
Table of Comparison
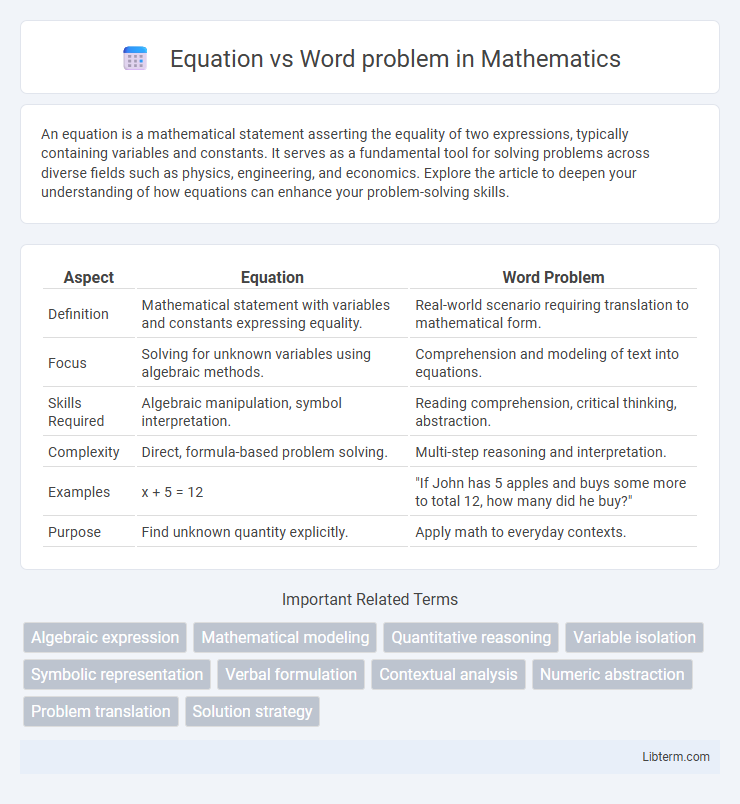
| Aspect | Equation | Word Problem |
|---|---|---|
| Definition | Mathematical statement with variables and constants expressing equality. | Real-world scenario requiring translation to mathematical form. |
| Focus | Solving for unknown variables using algebraic methods. | Comprehension and modeling of text into equations. |
| Skills Required | Algebraic manipulation, symbol interpretation. | Reading comprehension, critical thinking, abstraction. |
| Complexity | Direct, formula-based problem solving. | Multi-step reasoning and interpretation. |
| Examples | x + 5 = 12 | "If John has 5 apples and buys some more to total 12, how many did he buy?" |
| Purpose | Find unknown quantity explicitly. | Apply math to everyday contexts. |
Understanding Equations: A Quick Overview
Understanding equations involves recognizing them as mathematical statements showing the equality of two expressions, often containing variables representing unknown values. Word problems require translating real-world scenarios into equations by identifying key information, relationships, and constraints embedded in the text. Mastery of equations facilitates solving word problems by enabling the formulation of precise mathematical models from narrative descriptions.
Defining Word Problems in Mathematics
Word problems in mathematics translate real-life scenarios into verbal descriptions requiring mathematical solutions. These problems involve identifying relevant information, formulating equations, and applying problem-solving strategies. Defining word problems emphasizes understanding context and variables to accurately model and solve practical situations.
Key Differences Between Equations and Word Problems
Equations represent mathematical relationships using symbols and numbers, allowing for straightforward manipulation and solving. Word problems require translating real-world scenarios into equations, involving comprehension of context, identifying relevant information, and forming corresponding mathematical expressions. The key difference lies in equations presenting abstract numerical relationships directly, while word problems demand interpreting language to create those equations.
Translating Word Problems into Equations
Translating word problems into equations involves identifying variables representing unknown quantities and expressing relationships using mathematical symbols. Key steps include analyzing the problem statement, isolating relevant data, and formulating algebraic expressions that reflect those relationships. Mastery of this skill enhances problem-solving accuracy and efficiency across diverse math topics.
The Role of Variables in Equations and Word Problems
Variables in equations represent unknown values that can be manipulated algebraically to find precise solutions, serving as critical placeholders for numbers. In word problems, variables function as symbolic representations of real-world quantities, facilitating the translation of complex scenarios into mathematical expressions. Their correct identification and interpretation are essential for constructing accurate models and solving contextual questions effectively.
Common Challenges Students Face
Students often struggle with translating word problems into accurate equations due to difficulties in identifying relevant information and mathematical operations required. Misinterpretation of problem context can lead to errors in setting up equations, causing incorrect solutions. Building strong problem-solving skills and practicing the connection between verbal descriptions and mathematical expressions are essential to overcoming these challenges.
Step-by-Step Strategies for Solving Word Problems
Breaking down word problems involves identifying key information and translating it into mathematical expressions or equations. Employing strategies such as highlighting important data, defining variables clearly, and writing step-by-step equations helps in systematic problem-solving. Practicing consistent substitution and verification of results ensures accuracy and reinforces understanding of the relationship between the problem context and the equation.
The Importance of Context in Word Problems
Context in word problems plays a crucial role in translating real-life situations into mathematical equations, ensuring meaningful and accurate problem-solving. Understanding the scenario helps identify relevant variables, constraints, and relationships, leading to the formulation of precise equations. Without contextual comprehension, solving word problems can result in misinterpretation and incorrect solutions despite mathematical skills.
Real-World Applications: When to Use Equations vs. Word Problems
Equations are ideal for solving precise mathematical tasks that require clear numerical relationships, such as calculating interest rates or determining dimensions in architecture. Word problems excel in real-world contexts where multiple variables and situational understanding are necessary, like budgeting household expenses or analyzing business profits. Choosing between equations and word problems depends on whether the problem demands exact computation or interpretation of a complex scenario.
Tips for Mastering Both Equations and Word Problems
Mastering both equations and word problems requires a strong grasp of algebraic concepts and the ability to translate real-world scenarios into mathematical expressions. Practice identifying keywords and quantities in word problems to construct accurate equations, enhancing problem-solving efficiency. Consistent review of foundational principles and solving diverse problem types build confidence and improve analytical skills.
Equation Infographic
 libterm.com
libterm.com