Algebraic expressions consist of variables, constants, and arithmetic operations, allowing you to represent complex mathematical relationships succinctly. Mastering algebraic manipulation is essential for solving equations, modeling real-world problems, and advancing in mathematics. Explore the full article to deepen your understanding and improve your problem-solving skills.
Table of Comparison
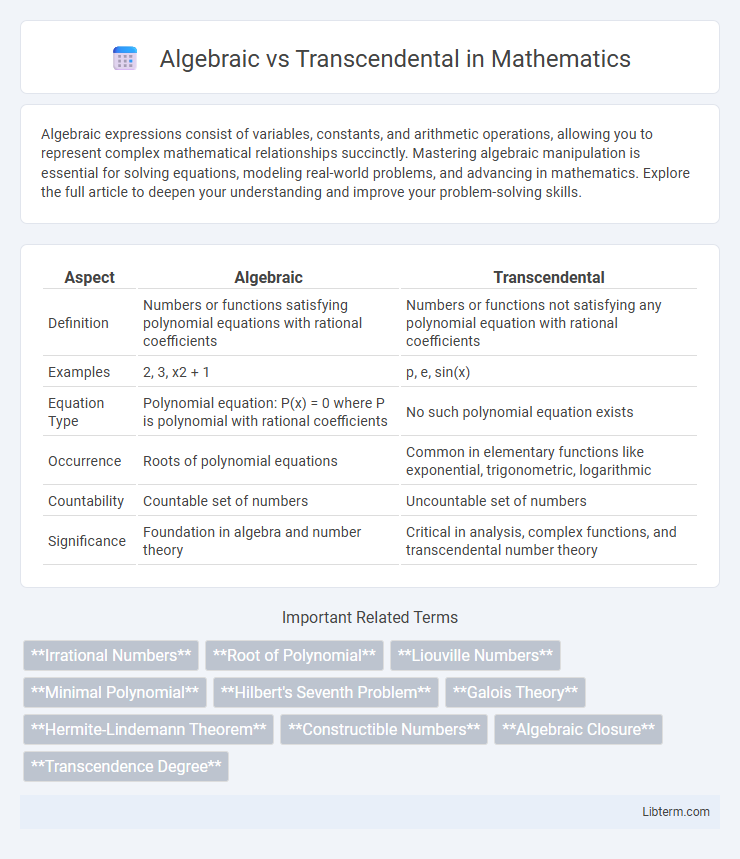
| Aspect | Algebraic | Transcendental |
|---|---|---|
| Definition | Numbers or functions satisfying polynomial equations with rational coefficients | Numbers or functions not satisfying any polynomial equation with rational coefficients |
| Examples | 2, 3, x2 + 1 | p, e, sin(x) |
| Equation Type | Polynomial equation: P(x) = 0 where P is polynomial with rational coefficients | No such polynomial equation exists |
| Occurrence | Roots of polynomial equations | Common in elementary functions like exponential, trigonometric, logarithmic |
| Countability | Countable set of numbers | Uncountable set of numbers |
| Significance | Foundation in algebra and number theory | Critical in analysis, complex functions, and transcendental number theory |
Introduction to Algebraic and Transcendental Numbers
Algebraic numbers are roots of non-zero polynomial equations with rational coefficients, encompassing both rational numbers and many irrational numbers such as the square root of 2. Transcendental numbers, in contrast, are not solutions to any such polynomial equation, with famous examples including p and e, which cannot be expressed algebraically. Understanding the distinction between algebraic and transcendental numbers is fundamental in number theory and has profound implications in fields like complex analysis and cryptography.
Defining Algebraic Numbers
Algebraic numbers are defined as complex numbers that are roots of non-zero polynomial equations with rational coefficients, distinguishing them from transcendental numbers which are not solutions to any such polynomial. These algebraic numbers include integers, rational numbers, and roots of polynomials like x2 - 2 = 0, representing a broad class within number theory. Understanding the criteria for algebraic numbers is fundamental in fields such as algebra, number theory, and computational mathematics.
Understanding Transcendental Numbers
Transcendental numbers are defined as real or complex numbers that are not roots of any non-zero polynomial equation with rational coefficients, setting them apart from algebraic numbers which solve such equations. Famous examples include p (pi) and e (Euler's number), both proven transcendental through advanced mathematical proofs like Lindemann-Weierstrass theorem. Understanding transcendental numbers is crucial in fields like number theory and algebra, as they reveal the limitations of algebraic methods and influence concepts of computability and complexity in mathematics.
Key Differences Between Algebraic and Transcendental Numbers
Algebraic numbers are solutions to non-zero polynomial equations with integer coefficients, while transcendental numbers cannot be expressed as roots of any such polynomial, making them non-algebraic by definition. Key differences include that algebraic numbers are countable and often include rational and some irrational numbers like 2, whereas transcendental numbers such as p and e are uncountable and exhibit a higher level of complexity in number theory. This distinction is fundamental in fields like algebra and analysis, influencing the classification and properties of real and complex numbers.
Historical Discoveries and Famous Examples
Algebraic numbers, rooted in solutions to polynomial equations with rational coefficients, have been studied since ancient times with notable examples like the square root of 2 and the golden ratio. Transcendental numbers, defined as numbers not algebraic and not satisfying any polynomial equation with rational coefficients, were first proven to exist by Joseph Liouville in the 19th century, with famous examples including p (pi) and e (Euler's number). The historical progression from understanding algebraic numbers to establishing the transcendence of constants like p by Ferdinand von Lindemann in 1882 marks a significant milestone in mathematical history.
Algebraic Numbers: Properties and Applications
Algebraic numbers are roots of non-zero polynomial equations with rational coefficients, distinguishing them from transcendental numbers that are not solutions to any such polynomial. Key properties include closure under addition, subtraction, multiplication, and division (except by zero), making them form a field known as the algebraic closure of the rationals. Applications of algebraic numbers span number theory, cryptography, and solving polynomial equations, enabling advances in computational algebra systems and algorithm design.
Transcendental Numbers: Properties and Importance
Transcendental numbers, such as p and e, are defined by their inability to satisfy any non-zero polynomial equation with rational coefficients, setting them apart from algebraic numbers. Their unique properties include infinite non-repeating decimal expansions and crucial roles in fields like number theory, complex analysis, and mathematical constants modeling. The transcendence of numbers like p ensures the impossibility of classical problems such as squaring the circle, underlining their importance in both theoretical mathematics and practical applications.
Real-World Uses and Implications
Algebraic numbers, which are roots of polynomial equations with rational coefficients, are crucial in cryptography, error-correcting codes, and computer algorithms due to their predictable and computable nature. Transcendental numbers, such as p and e, appear in natural phenomena modeling, including engineering, physics, and finance, where continuous growth, wave patterns, and probabilistic calculations dominate. Understanding the distinction enhances numerical methods, optimizing solutions for real-world problems in technology and scientific research.
Challenges in Identifying Transcendental Numbers
Identifying transcendental numbers presents significant challenges due to their inherent complexity and the absence of general criteria for classification. Unlike algebraic numbers, which satisfy polynomial equations with integer coefficients, transcendental numbers cannot be roots of any such polynomial, making their distinction highly non-trivial. The difficulty is further compounded by the scarcity of explicit examples, with classic transcendental numbers like p and e being among the few proven cases.
Conclusion: The Ongoing Exploration in Mathematics
Algebraic numbers, defined as roots of non-zero polynomial equations with rational coefficients, contrast fundamentally with transcendental numbers, which cannot satisfy any such polynomial equation. The ongoing exploration in mathematics continues to reveal deeper insights into these classifications, advancing fields like number theory and complex analysis with implications for computational methods and theoretical frameworks. Research in transcendental number theory remains vibrant, highlighting unresolved questions about the distribution and properties of transcendental numbers within the real and complex number systems.
Algebraic Infographic
 libterm.com
libterm.com