A probability measure assigns a number between 0 and 1 to events in a sample space, quantifying the likelihood of occurrence under uncertainty. It follows specific axioms such as non-negativity, normalization, and countable additivity that ensure consistent probability assignments. Explore the detailed properties and applications of probability measures through the rest of this article to enhance your understanding.
Table of Comparison
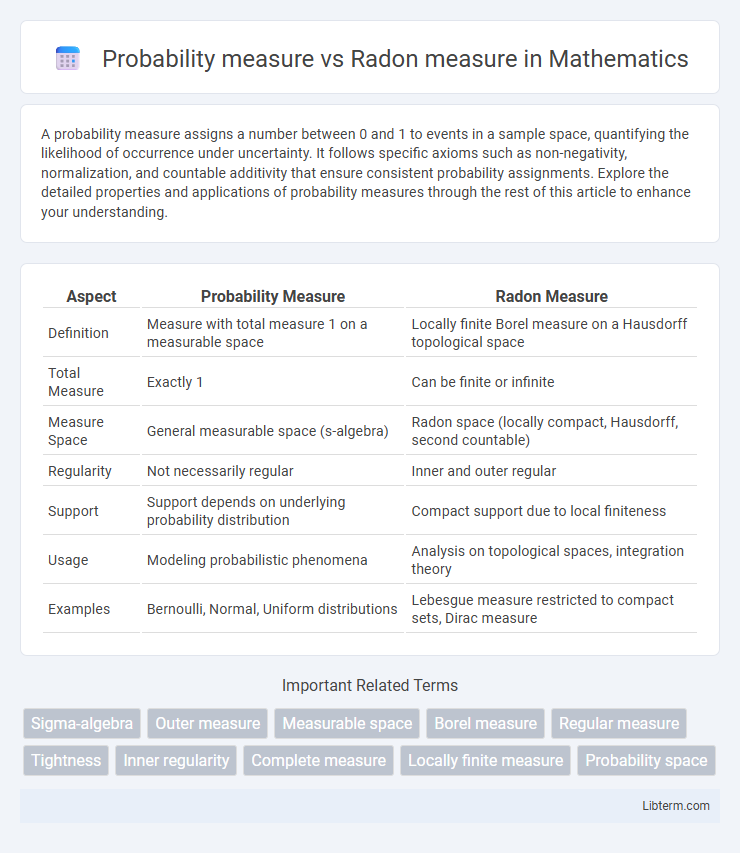
| Aspect | Probability Measure | Radon Measure |
|---|---|---|
| Definition | Measure with total measure 1 on a measurable space | Locally finite Borel measure on a Hausdorff topological space |
| Total Measure | Exactly 1 | Can be finite or infinite |
| Measure Space | General measurable space (s-algebra) | Radon space (locally compact, Hausdorff, second countable) |
| Regularity | Not necessarily regular | Inner and outer regular |
| Support | Support depends on underlying probability distribution | Compact support due to local finiteness |
| Usage | Modeling probabilistic phenomena | Analysis on topological spaces, integration theory |
| Examples | Bernoulli, Normal, Uniform distributions | Lebesgue measure restricted to compact sets, Dirac measure |
Introduction to Probability and Radon Measures
Probability measures are specialized Radon measures defined on sigma-algebras with total mass equal to one, ensuring they represent valid distributions of random events. Radon measures generalize this concept by allowing finite or infinite total mass and are characterized by their inner regularity on locally compact Hausdorff spaces. Understanding the interplay between probability and Radon measures is fundamental in fields such as stochastic analysis and measure-theoretic probability.
Defining Probability Measures
A probability measure is a specific type of Radon measure defined on a measurable space that assigns a total measure of one to the entire space, ensuring the measure represents a valid probability distribution. Radon measures are locally finite and inner regular Borel measures defined on Hausdorff topological spaces, used to handle more general integration and limit processes. Defining probability measures requires satisfying countable additivity and non-negativity while normalizing the measure to one, contrasting with Radon measures which do not necessarily adhere to this normalization but emphasize topological compatibility.
Understanding Radon Measures
Radon measures extend probability measures by defining finite measures on locally compact Hausdorff spaces with inner regularity and outer regularity properties, enabling analysis beyond sigma-finite constraints. Unlike probability measures, which allocate total mass one to measurable sets, Radon measures facilitate integration and approximation of functions through compact subsets, crucial in functional analysis and topology. Understanding Radon measures involves grasping their tightness and regularity, ensuring measurable sets can be approximated from inside by compact sets and from outside by open sets, enhancing measure-theoretic precision on complex spaces.
Key Properties of Probability Measures
Probability measures are specialized Radon measures defined on sigma-algebras with total measure equal to one, ensuring normalization and finiteness while maintaining inner regularity and local finiteness. These measures assign probabilities to events, satisfying countable additivity and measurability, making them essential for modeling uncertainty in stochastic processes. Radon measures extend beyond probability measures by allowing infinite total mass and providing flexibility in analysis on locally compact Hausdorff spaces.
Essential Properties of Radon Measures
Radon measures are defined on locally compact Hausdorff spaces and are characterized by being inner regular, meaning their measure of any Borel set can be approximated from within by compact sets. These measures are also locally finite, assigning finite measure to all compact sets, which distinguishes them from probability measures that are normalized to one on the entire space. The essential property of Radon measures includes tightness, ensuring that for any positive e, a compact set exists whose measure exceeds the total measure minus e, enabling robust integration and analysis in functional spaces.
Major Differences Between Probability and Radon Measures
Probability measures are defined on a sigma-algebra and assign a total measure of one, representing the likelihood of events within a given probability space. Radon measures are defined on the Borel sigma-algebra of a topological space and are locally finite, inner regular, and can take any non-negative value, often used in analysis and geometric measure theory. The major difference lies in their scope and constraints: probability measures are normalized and deal with stochastic processes, while Radon measures are more general, handling measure extensions on topological spaces without the normalization requirement.
Examples Illustrating Each Measure
Probability measures assign values between 0 and 1 to events within a sigma-algebra, exemplified by the uniform distribution on the interval [0, 1] where each subinterval's measure corresponds to its length. Radon measures extend this concept by being locally finite and inner regular on a topological space, illustrated by the Lebesgue measure on R, which assigns measure based on length but also applies to more complex sets. While probability measures are a special case of Radon measures with total measure one, Radon measures include broader examples like Dirac measures concentrated at a point, assigning full mass to singleton sets.
Applications in Mathematics and Beyond
Probability measures quantify the likelihood of events within a probabilistic framework, essential for modeling uncertainty in statistics, stochastic processes, and machine learning. Radon measures extend beyond probability by providing a rigorous tool for integration on locally compact Hausdorff spaces, crucial in functional analysis, geometric measure theory, and partial differential equations. Their applications intersect in areas such as optimal transport, ergodic theory, and quantitative finance, where both probabilistic interpretation and measure-theoretic rigor are required.
Relationship and Intersections Between the Two
Probability measures are specialized Radon measures normalized so that the total measure equals one, forming a subset within the broader class of Radon measures on locally compact Hausdorff spaces. Both measures are defined on Borel s-algebras and share properties like inner regularity and local finiteness, ensuring consistency in integration and convergence theories. The intersection between them lies in scenarios where Radon measures represent distributions that can be scaled to probability measures, facilitating applications in stochastic processes and measure-theoretic probability.
Conclusion: Choosing the Right Measure
Selecting between a probability measure and a Radon measure depends on the application context and the underlying space characteristics; probability measures are ideal for modeling uncertainty in finite or sigma-finite spaces with total mass one. Radon measures provide greater flexibility for locally compact Hausdorff spaces, accommodating infinite measures while retaining regularity properties essential for analysis. Understanding the interplay between normalization, support, and regularity ensures the selection of a measure that aligns with theoretical requirements and practical needs.
Probability measure Infographic
 libterm.com
libterm.com