The universal enveloping algebra is a fundamental construction in Lie algebra theory that associates an associative algebra to any given Lie algebra, preserving its structure while enabling broader algebraic operations. It plays a critical role in representation theory by allowing Lie algebra representations to be studied through module theory over associative algebras. Discover how the universal enveloping algebra bridges these concepts and its significance in advanced mathematical frameworks in the rest of this article.
Table of Comparison
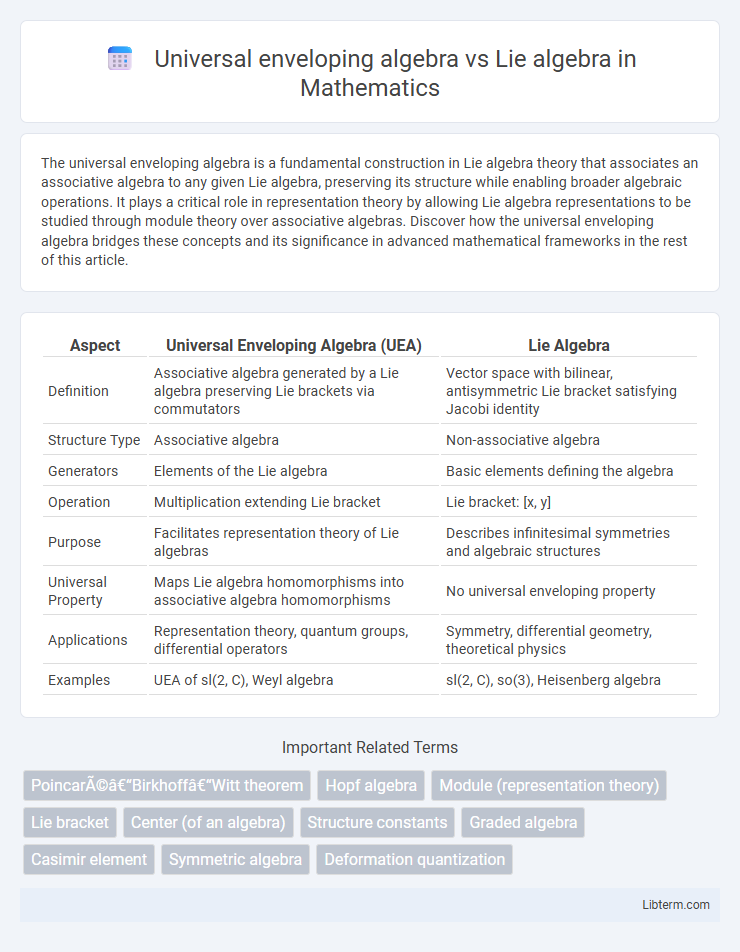
| Aspect | Universal Enveloping Algebra (UEA) | Lie Algebra |
|---|---|---|
| Definition | Associative algebra generated by a Lie algebra preserving Lie brackets via commutators | Vector space with bilinear, antisymmetric Lie bracket satisfying Jacobi identity |
| Structure Type | Associative algebra | Non-associative algebra |
| Generators | Elements of the Lie algebra | Basic elements defining the algebra |
| Operation | Multiplication extending Lie bracket | Lie bracket: [x, y] |
| Purpose | Facilitates representation theory of Lie algebras | Describes infinitesimal symmetries and algebraic structures |
| Universal Property | Maps Lie algebra homomorphisms into associative algebra homomorphisms | No universal enveloping property |
| Applications | Representation theory, quantum groups, differential operators | Symmetry, differential geometry, theoretical physics |
| Examples | UEA of sl(2, C), Weyl algebra | sl(2, C), so(3), Heisenberg algebra |
Introduction to Lie Algebras
Lie algebras are algebraic structures essential in studying the properties of continuous symmetry and differentiable manifolds, characterized by the Lie bracket operation that satisfies bilinearity, antisymmetry, and the Jacobi identity. The universal enveloping algebra of a Lie algebra provides an associative algebra framework that encodes the Lie algebra's structure and facilitates representation theory through the Poincare-Birkhoff-Witt theorem, which ensures a canonical embedding of the Lie algebra into its enveloping algebra. Understanding the interplay between Lie algebras and their universal enveloping algebras enables deeper exploration of symmetries in geometry and physics, as well as advancements in modern algebraic theory.
Concept and Definition of Universal Enveloping Algebras
Universal enveloping algebras are associative algebras constructed from Lie algebras to encode their structure within a richer algebraic framework, enabling the application of module theory and representation theory. They arise as the quotient of the tensor algebra over a Lie algebra by the ideal generated by elements reflecting the Lie bracket, thus preserving the Lie algebra's commutation relations. This construction provides a universal property that maps any Lie algebra homomorphism into an associative algebra uniquely through the enveloping algebra, bridging Lie algebras and associative algebraic structures.
Algebraic Structures: Comparing Lie and Universal Enveloping Algebras
Lie algebras consist of a vector space equipped with a Lie bracket that satisfies antisymmetry and the Jacobi identity, forming a foundational algebraic structure for studying symmetry and conservation laws. Universal enveloping algebras are associative algebras constructed from Lie algebras, capturing their structure while enabling the representation of Lie algebra elements as non-commuting polynomial-like expressions. The universal enveloping algebra serves as a bridge between non-associative Lie algebras and associative algebra theory, allowing one to leverage powerful tools from associative algebra for representation and module theory.
Construction of the Universal Enveloping Algebra
The construction of the universal enveloping algebra \( U(\mathfrak{g}) \) of a Lie algebra \( \mathfrak{g} \) involves forming the tensor algebra \( T(\mathfrak{g}) \) over the underlying vector space of \( \mathfrak{g} \) and then quotienting by the two-sided ideal generated by elements of the form \( x \otimes y - y \otimes x - [x,y] \) for all \( x,y \in \mathfrak{g} \). This construction ensures that the Lie bracket in \( \mathfrak{g} \) is encoded as the commutator in \( U(\mathfrak{g}) \), allowing the embedding of the Lie algebra into an associative algebra. The Poincare-Birkhoff-Witt (PBW) theorem further guarantees that \( U(\mathfrak{g}) \) is a filtered algebra whose associated graded algebra is isomorphic to the symmetric algebra \( S(\mathfrak{g}) \), preserving the structure of \( \mathfrak{g} \) within \( U(\mathfrak{g}) \).
The Universal Property in Enveloping Algebras
The universal enveloping algebra of a Lie algebra \( \mathfrak{g} \) is characterized by its universal property: any Lie algebra homomorphism from \( \mathfrak{g} \) to the associative algebra \( A \) extends uniquely to an algebra homomorphism from the universal enveloping algebra \( U(\mathfrak{g}) \) to \( A \). This property ensures \( U(\mathfrak{g}) \) serves as the initial object in the category of associative algebras containing \( \mathfrak{g} \) as a Lie subalgebra, preserving the Lie bracket via commutators. The universal property facilitates the embedding of Lie algebra representations into module theory over associative algebras, making \( U(\mathfrak{g}) \) a central tool in representation theory and algebraic constructions.
Relationship Between Lie Algebras and Their Universal Enveloping Algebras
The universal enveloping algebra of a Lie algebra is an associative algebra that contains the Lie algebra as a subspace, allowing the Lie bracket to be expressed as a commutator in the enveloping algebra. This construction provides a bridge between non-associative Lie algebras and associative algebras, enabling representation theory of Lie algebras to be studied via modules over their universal enveloping algebras. The Poincare-Birkhoff-Witt (PBW) theorem guarantees an injective Lie algebra homomorphism into its universal enveloping algebra, preserving the structure and ensuring the universal property of enveloping algebras.
Representations: Lie Algebra vs Universal Enveloping Algebra
Lie algebra representations correspond to linear actions preserving the Lie bracket structure, enabling the study of infinitesimal symmetries via modules over the algebra. Universal enveloping algebras extend Lie algebras by providing associative algebra structures that facilitate representing Lie algebra elements as operators acting on vector spaces through algebra homomorphisms. This translation allows any Lie algebra representation to be viewed as a module over its universal enveloping algebra, unifying and enriching the framework for analyzing representation theory.
Applications in Mathematics and Physics
Universal enveloping algebras play a crucial role in representation theory by enabling the study of Lie algebra modules through associative algebra techniques, facilitating the classification of irreducible representations. In mathematical physics, they provide the algebraic framework for quantization processes and symmetry analysis in quantum mechanics and quantum field theory. Lie algebras themselves underpin the study of continuous symmetries and conservation laws, foundational in both classical mechanics and gauge theories.
Key Differences and Similarities
The Universal Enveloping Algebra (UEA) of a Lie algebra is an associative algebra that encodes the Lie algebra's structure while allowing the use of associative algebra techniques, contrasting with the Lie algebra's non-associative, bilinear bracket operation satisfying the Jacobi identity. Both structures share the same underlying vector space and preserve the Lie bracket via commutators in the UEA, enabling representations of Lie algebras to be studied through module theory over the UEA. Key differences include the UEA's universal property facilitating homomorphisms to associative algebras and the Lie algebra's role as the infinitesimal object capturing symmetry and derivations, whereas the UEA provides a framework for constructing representations and analyzing algebraic properties in a broader associative context.
Conclusion: Insights and Future Directions
Universal enveloping algebras encapsulate Lie algebras by providing associative algebra structures that facilitate representation theory and module construction. Exploring deeper connections between their homological properties may reveal novel algebraic invariants and categorification frameworks. Future research aims to harness these insights for advancements in quantum groups, noncommutative geometry, and deformation theory.
Universal enveloping algebra Infographic
 libterm.com
libterm.com