A sigma-finite measure is a fundamental concept in measure theory where a measure space can be decomposed into a countable union of measurable sets, each having finite measure. This property generalizes finiteness and plays a crucial role in various applications, including integration theory and probability. Explore the full article to understand how sigma-finite measures underpin key results and their practical significance for your studies.
Table of Comparison
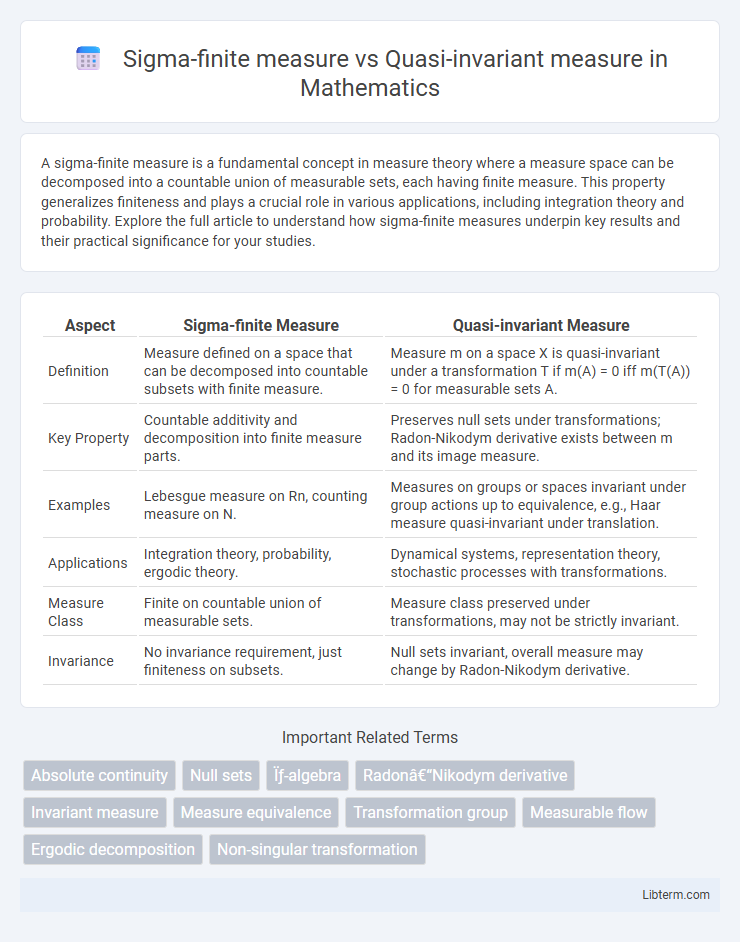
| Aspect | Sigma-finite Measure | Quasi-invariant Measure |
|---|---|---|
| Definition | Measure defined on a space that can be decomposed into countable subsets with finite measure. | Measure m on a space X is quasi-invariant under a transformation T if m(A) = 0 iff m(T(A)) = 0 for measurable sets A. |
| Key Property | Countable additivity and decomposition into finite measure parts. | Preserves null sets under transformations; Radon-Nikodym derivative exists between m and its image measure. |
| Examples | Lebesgue measure on Rn, counting measure on N. | Measures on groups or spaces invariant under group actions up to equivalence, e.g., Haar measure quasi-invariant under translation. |
| Applications | Integration theory, probability, ergodic theory. | Dynamical systems, representation theory, stochastic processes with transformations. |
| Measure Class | Finite on countable union of measurable sets. | Measure class preserved under transformations, may not be strictly invariant. |
| Invariance | No invariance requirement, just finiteness on subsets. | Null sets invariant, overall measure may change by Radon-Nikodym derivative. |
Introduction to Measure Theory
Sigma-finite measures are fundamental in measure theory, defined by the existence of a countable partition of the space into measurable sets with finite measure, facilitating integration and convergence theorems. Quasi-invariant measures arise in the study of group actions on measure spaces, where the measure changes by a Radon-Nikodym derivative but remains absolutely continuous with respect to its image under the action. Understanding these concepts is crucial for advanced analysis, particularly in ergodic theory and representation theory, as they provide frameworks for dealing with infinite measures and transformations preserving measure classes.
Defining Sigma-finite Measures
Sigma-finite measures are defined on a measurable space where the entire space can be decomposed into a countable union of measurable subsets, each having finite measure. This property allows for the application of important measure-theoretic results such as the Radon-Nikodym theorem and Fubini's theorem in broader contexts. Unlike quasi-invariant measures, which emphasize invariance properties under group actions, sigma-finite measures primarily focus on manageable decompositions to extend classical integration and measure operations.
Understanding Quasi-invariant Measures
Quasi-invariant measures differ from sigma-finite measures by allowing transformations that preserve the measure class without necessarily preserving the measure itself, enabling the study of group actions and ergodic theory in more general settings. Unlike sigma-finite measures, which decompose the space into countable measurable subsets with finite measure, quasi-invariant measures are characterized by their Radon-Nikodym derivatives under transformations. Understanding quasi-invariant measures involves analyzing how measures change under transformations while maintaining absolute continuity, which is crucial in harmonic analysis and dynamic systems.
Key Differences Between Sigma-finite and Quasi-invariant Measures
Sigma-finite measures are characterized by their ability to decompose the entire space into a countable union of measurable sets with finite measure, facilitating the application of measure-theoretic tools like the Radon-Nikodym theorem. In contrast, quasi-invariant measures maintain absolute continuity under group actions or transformations, ensuring measure changes through a Radon-Nikodym derivative but do not necessarily allow for such decomposition. The key difference lies in sigma-finiteness being a structural property enabling measure decomposition, whereas quasi-invariance describes stability of the measure under transformations without guaranteeing sigma-finiteness.
Properties of Sigma-finite Measures
Sigma-finite measures decompose a space into countably many measurable subsets with finite measure, facilitating integration and limiting the complexity of measure-theoretic analysis. These measures ensure the applicability of key theorems like the Radon-Nikodym and Fubini-Tonelli, requiring only sigma-finiteness rather than finiteness. Their structure contrasts with quasi-invariant measures, which preserve measure-null sets under group actions but do not necessarily admit such countable decompositions.
Applications of Sigma-finite Measures
Sigma-finite measures provide a critical framework for decomposing complex measure spaces into countable unions of finite measure sets, enabling the tractable analysis of probability distributions and integration in various mathematical and applied fields. They facilitate the extension of classical theorems in measure theory, such as the Radon-Nikodym derivative and Fubini's theorem, which are essential in stochastic processes, statistical mechanics, and ergodic theory. Quasi-invariant measures, by contrast, play a significant role in dynamical systems and representation theory, where invariance under group actions is relaxed, but the applications of sigma-finite measures remain foundational for rigorous probabilistic modeling and functional analysis.
Characteristic Features of Quasi-invariant Measures
Quasi-invariant measures preserve null sets under group actions, meaning the measure of a set is zero if and only if its image under the group action is also of measure zero, contrasting with sigma-finite measures that are decomposable into countable unions of finite measure sets. The Radon-Nikodym derivative plays a crucial role in quasi-invariant measures by quantifying how the measure transforms under the group action, reflecting quasi-invariance rather than strict invariance. Quasi-invariant measures often arise in representation theory and ergodic theory, where transformations alter sets without changing their nullity, enabling analysis of dynamical systems beyond the scope of sigma-finiteness.
Use Cases for Quasi-invariant Measures
Quasi-invariant measures are essential in ergodic theory and representation theory, especially for studying group actions on measure spaces where invariance under transformations is relaxed to absolute continuity. These measures find use in harmonic analysis on locally compact groups, infinite-dimensional analysis, and the construction of unitary representations, enabling the examination of dynamical systems with nontrivial symmetries. Sigma-finite measures, while fundamental for measure-theoretic foundations and integration, often lack the flexibility required for analyzing transformations with quasi-invariance properties critical in these advanced mathematical frameworks.
Sigma-finite vs Quasi-invariant: When to Use Each
Sigma-finite measures are essential in measure theory when decomposing a space into countable subsets with finite measure simplifies integration and probability analysis, making them ideal for applications in classical probability and standard Lebesgue measure spaces. Quasi-invariant measures are crucial in dynamical systems and harmonic analysis, where measures change in an absolutely continuous manner under group actions, retaining the structure needed for Radon-Nikodym derivatives and invariant properties. Use sigma-finite measures for foundational measure decomposition and apply quasi-invariant measures when studying transformations or symmetries involving measure-preserving or absolutely continuous variations.
Conclusion and Implications for Further Research
Sigma-finite measures provide a foundation for measure theory by ensuring measures can be decomposed into countable collections of finite-measure sets, facilitating integration and probability analysis. Quasi-invariant measures extend this framework by allowing transformations that alter measures in a controlled, absolutely continuous manner, enabling advanced study in ergodic theory and group actions. Future research could explore the interplay between sigma-finiteness and quasi-invariance in non-standard spaces, deepening understanding of dynamic systems and invariant measures in infinite-dimensional contexts.
Sigma-finite measure Infographic
 libterm.com
libterm.com