Recursive language enables complex and infinite sentence formation by embedding phrases within phrases, illustrating the flexibility of human communication. This characteristic is fundamental to syntax and natural language processing, allowing nuanced expression and understanding. Explore the article to uncover how recursion shapes language and impacts your communication skills.
Table of Comparison
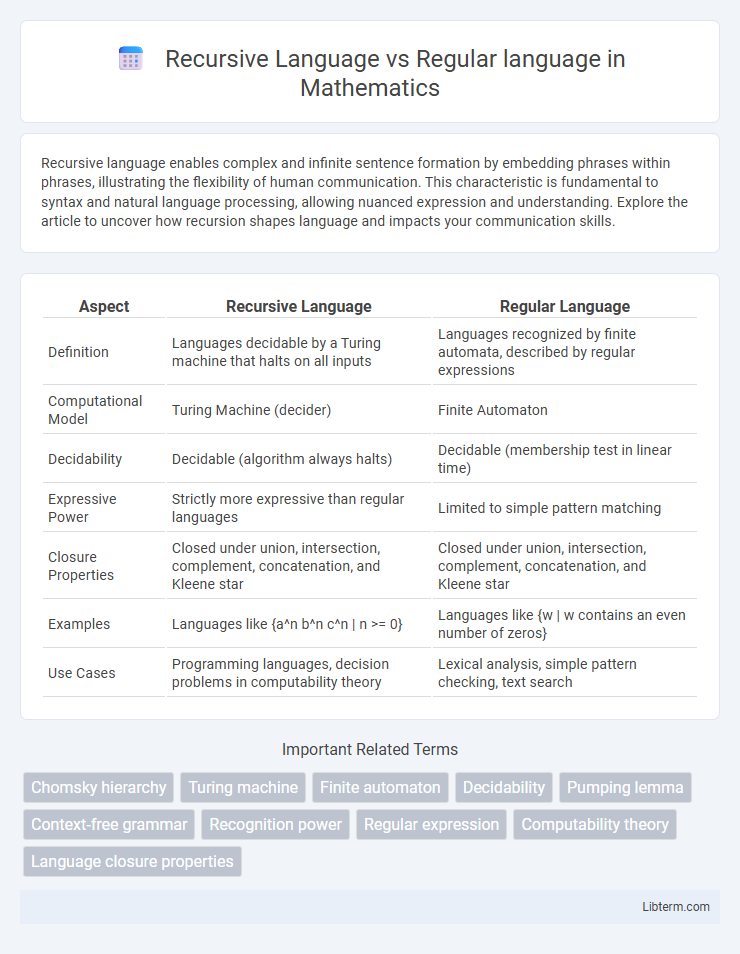
| Aspect | Recursive Language | Regular Language |
|---|---|---|
| Definition | Languages decidable by a Turing machine that halts on all inputs | Languages recognized by finite automata, described by regular expressions |
| Computational Model | Turing Machine (decider) | Finite Automaton |
| Decidability | Decidable (algorithm always halts) | Decidable (membership test in linear time) |
| Expressive Power | Strictly more expressive than regular languages | Limited to simple pattern matching |
| Closure Properties | Closed under union, intersection, complement, concatenation, and Kleene star | Closed under union, intersection, complement, concatenation, and Kleene star |
| Examples | Languages like {a^n b^n c^n | n >= 0} | Languages like {w | w contains an even number of zeros} |
| Use Cases | Programming languages, decision problems in computability theory | Lexical analysis, simple pattern checking, text search |
Introduction to Recursive and Regular Languages
Recursive languages are a class of formal languages recognizable by a Turing machine that halts on all inputs, ensuring decidability and effective membership testing. Regular languages, defined by finite automata or regular expressions, represent a simpler class characterized by limited computational power and closure properties under operations like union, intersection, and complement. Understanding the hierarchy between recursive and regular languages is fundamental in automata theory, highlighting the trade-offs between computational complexity and expressiveness.
Definition of Recursive Languages
Recursive languages, also known as decidable languages, are sets of strings for which membership can be determined by a Turing machine that halts on every input. These languages are defined by the existence of a total computable function that decides whether a given string belongs to the language or not. Recursive languages encompass all regular and context-free languages, but also extend beyond them, providing a broader framework for algorithmic decidability in formal language theory.
Definition of Regular Languages
Regular languages are formal languages recognizable by finite automata and described by regular expressions, characterized by their limited memory and inability to handle nested or recursive structures. In contrast, recursive languages encompass a broader class, defined as those decidable by a Turing machine that halts on all inputs, allowing the recognition of more complex patterns beyond regular languages. Understanding the distinction between regular and recursive languages is fundamental in formal language theory, automata theory, and computational complexity.
Key Differences Between Recursive and Regular Languages
Recursive languages are a class of formal languages that can be decided by a Turing machine which halts on all inputs, ensuring a definitive yes or no answer. Regular languages are simpler, defined by finite automata and regular expressions, and lack the computational power to recognize nested or recursive patterns. The key difference lies in their computational complexity: recursive languages encompass a broader set of problems with potentially unbounded memory use, whereas regular languages are limited to finite memory and simpler pattern recognition.
Formal Properties of Recursive Languages
Recursive languages are characterized by their decidability, meaning there exists a Turing machine that halts and accepts or rejects every input string definitively. These languages are closed under union, intersection, complementation, and set difference, confirming their robust algebraic structure. The formal properties of recursive languages ensure that membership testing is always computable, distinguishing them from recursively enumerable languages, which may not guarantee halting for inputs outside the language.
Formal Properties of Regular Languages
Regular languages are defined by their recognition through finite automata and can be described using regular expressions, ensuring closure under operations like union, concatenation, and Kleene star. Their key formal property is decidability, meaning membership, emptiness, and equivalence problems can be efficiently solved. Recursive languages, by contrast, are recognized by Turing machines that always halt, making them strictly more powerful but less constrained in closure properties compared to regular languages.
Examples of Recursive Languages
Recursive languages, also known as decidable languages, include examples such as the set of balanced parentheses, palindromes over a given alphabet, and arithmetic expressions with properly matched operators and operands. These languages can be recognized by Turing machines that always halt, ensuring a decision procedure exists for membership testing. Their decidability contrasts with some context-free and non-regular languages that are not recursive, highlighting the computational power required for their recognition.
Examples of Regular Languages
Regular languages include patterns such as strings containing only a's and b's with a fixed number of repetitions, like (a|b)* representing all possible combinations of a and b. Examples also extend to simple regular expressions such as a(b|c)*, which denotes strings beginning with 'a' followed by any combination of 'b' and 'c'. These languages can be recognized by finite automata, differentiating them from recursive languages that require more computational power, like context-free or Turing-recognizable languages.
Applications in Computer Science and Automata Theory
Recursive languages are essential in computability theory, representing decision problems solvable by Turing machines that halt on all inputs, enabling reliable algorithmic verification. Regular languages, recognized by finite automata, are crucial for lexical analysis, pattern matching, and designing efficient text-processing algorithms due to their simplicity and closure properties. In automata theory, recursive languages help define decidable problems, while regular languages support parsing and compiler construction through their well-understood, resource-bounded recognition models.
Comparison Table: Recursive vs Regular Languages
Recursive languages are decidable by a Turing machine that always halts, while regular languages are recognized by finite automata with limited memory. Unlike regular languages that can be characterized by regular expressions and possess closure properties like union and intersection, recursive languages encompass a broader class, allowing algorithms to decide membership through more complex computations. The comparison highlights decidability, computational power, language class hierarchy, and the types of automata that recognize each language type.
Recursive Language Infographic
 libterm.com
libterm.com