Modular forms are complex functions that play a crucial role in number theory, particularly in understanding elliptic curves and partition functions. These functions exhibit symmetrical properties under the action of modular transformations, making them essential in modern mathematics and theoretical physics. Explore the article to discover how modular forms influence various fields and their applications in solving profound mathematical problems.
Table of Comparison
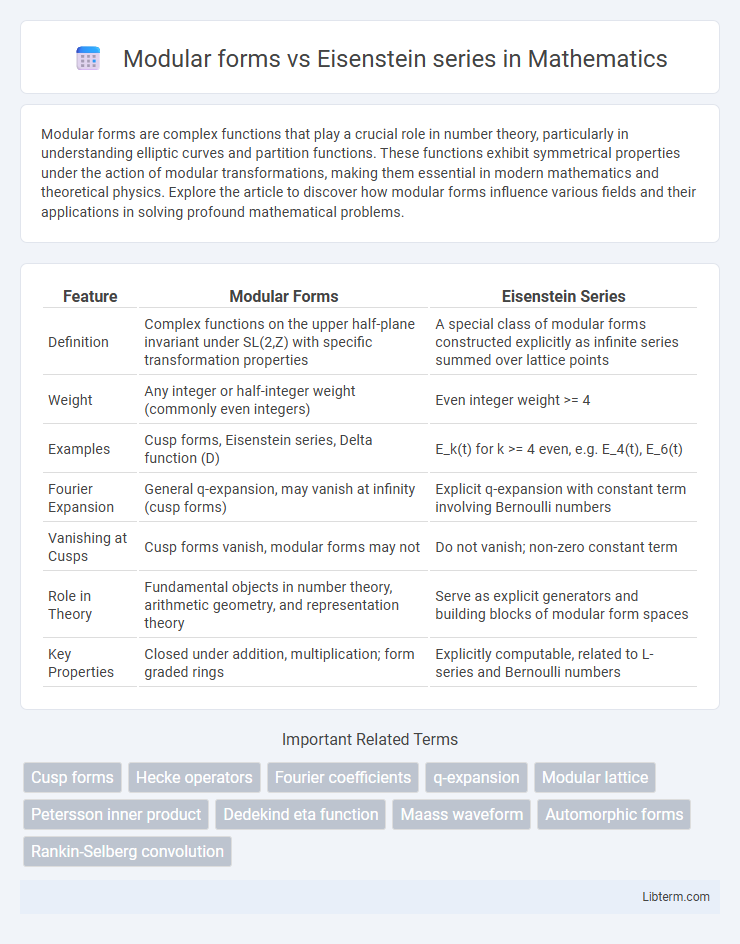
| Feature | Modular Forms | Eisenstein Series |
|---|---|---|
| Definition | Complex functions on the upper half-plane invariant under SL(2,Z) with specific transformation properties | A special class of modular forms constructed explicitly as infinite series summed over lattice points |
| Weight | Any integer or half-integer weight (commonly even integers) | Even integer weight >= 4 |
| Examples | Cusp forms, Eisenstein series, Delta function (D) | E_k(t) for k >= 4 even, e.g. E_4(t), E_6(t) |
| Fourier Expansion | General q-expansion, may vanish at infinity (cusp forms) | Explicit q-expansion with constant term involving Bernoulli numbers |
| Vanishing at Cusps | Cusp forms vanish, modular forms may not | Do not vanish; non-zero constant term |
| Role in Theory | Fundamental objects in number theory, arithmetic geometry, and representation theory | Serve as explicit generators and building blocks of modular form spaces |
| Key Properties | Closed under addition, multiplication; form graded rings | Explicitly computable, related to L-series and Bernoulli numbers |
Introduction to Modular Forms and Eisenstein Series
Modular forms are complex analytic functions on the upper half-plane exhibiting specific transformation properties under the action of the modular group SL(2, Z), with applications in number theory and mathematical physics. Eisenstein series form a fundamental class of modular forms constructed through infinite sums over lattice points, providing explicit examples and serving as building blocks for the space of modular forms. The Fourier expansion of Eisenstein series reveals critical connections to L-functions and arithmetic properties encoded in modular forms.
Historical Background and Development
Modular forms originated in the 19th century through the work of mathematicians like Dedekind and Hecke, developing as complex analytic functions invariant under the action of the modular group. Eisenstein series, introduced by Gotthold Eisenstein in the mid-19th century, represent some of the earliest explicit examples of modular forms, providing foundational insights into their Fourier expansions and transformation properties. The interplay between modular forms and Eisenstein series fueled advancements in number theory and facilitated the formulation of the modularity theorem, connecting arithmetic geometry and elliptic curves.
Fundamental Definitions and Key Properties
Modular forms are complex analytic functions on the upper half-plane satisfying specific transformation properties under the action of the modular group, exhibiting growth conditions at cusps. Eisenstein series are particular examples of modular forms, constructed as infinite series summing over lattice points, and serve as building blocks generating spaces of modular forms. Key properties include modular invariance, Fourier expansions at cusps, and connections to L-functions and number-theoretic coefficients.
Modular Forms: Structure and Examples
Modular forms are complex analytic functions defined on the upper half-plane that transform according to specific symmetry rules under the action of the modular group \(SL_2(\mathbb{Z})\), characterized by their weight and level. Their Fourier expansions reveal rich arithmetic properties and often include important structures such as cusp forms, which vanish at infinity, forming a vector space with finite dimension for fixed weight and level. Examples include classical modular forms like the Delta function and the Eisenstein series, with the latter serving as explicit, non-cuspidal modular forms that help generate the full space of modular forms.
Eisenstein Series: Definition and Explicit Construction
Eisenstein series are special cases of modular forms constructed explicitly by summing certain lattices in the complex plane, defined for even integer weights greater than two. Given a lattice \(\Lambda\), the Eisenstein series \(G_k(\tau)\) is defined as the series \(\sum_{\omega \in \Lambda \setminus \{0\}} \frac{1}{\omega^k}\), where \(\tau\) belongs to the upper half-plane and \(k\) is the weight. These series exhibit modular invariance under the action of the modular group \(\mathrm{SL}_2(\mathbb{Z})\) and provide explicit examples fundamental in the theory of modular forms.
Analytic and Algebraic Distinctions
Modular forms are complex analytic functions on the upper half-plane exhibiting transformation properties under the modular group, with Eisenstein series serving as explicit examples characterized by their construction from lattice sums and exhibiting simpler Fourier expansions. Analytically, Eisenstein series are non-cuspidal modular forms with distinguished growth behavior at cusps, contrasting cusp forms which vanish there and reflect deeper arithmetic properties. Algebraically, Eisenstein series correspond to elements in the space of modular forms with explicit q-expansions linked to divisor functions, whereas modular forms include both Eisenstein and cusp forms, forming a graded ring with rich structure connected to elliptic curves and Galois representations.
Relationship between Eisenstein Series and Modular Forms
Eisenstein series are a fundamental class of modular forms characterized by their explicit Fourier expansions and role as building blocks in the space of modular forms. Every Eisenstein series is a modular form for the full modular group SL(2, Z) or its congruence subgroups, serving to generate the ring of modular forms alongside cusp forms. The relationship between Eisenstein series and modular forms is pivotal in understanding modular form decompositions, L-functions, and arithmetic properties embedded in automorphic forms.
Fourier Expansions: Modular Forms vs. Eisenstein Series
Fourier expansions of modular forms typically involve sums of complex exponentials weighted by coefficients encoding deep arithmetic properties, while Eisenstein series exhibit explicit, well-structured Fourier expansions with coefficients expressed via divisor functions. The Fourier coefficients of Eisenstein series are often more accessible and serve as prototypes for understanding the growth and distribution of coefficients in general modular forms. This contrast highlights the role of Eisenstein series as building blocks, facilitating the decomposition and analysis of modular forms through their Fourier expansions.
Applications in Number Theory and Beyond
Modular forms, including Eisenstein series, play a critical role in number theory by providing tools to understand the distribution of prime numbers and congruences in arithmetic functions. Eisenstein series serve as explicit examples of modular forms that facilitate the construction of L-functions and the study of elliptic curves, pivotal in solving Diophantine equations and proving results like Fermat's Last Theorem. Beyond number theory, these functions appear in mathematical physics, particularly in string theory and conformal field theory, illustrating their broad applicability in modern mathematical sciences.
Summary: Comparative Insights and Future Directions
Modular forms represent a broad class of complex functions exhibiting specific transformation properties under the modular group, while Eisenstein series are explicit examples of modular forms constructed through summation over lattice points. Comparative analysis highlights Eisenstein series as foundational elements generating the space of modular forms and serving as key tools in number theory and arithmetic geometry. Future research aims to deepen the understanding of the interplay between modular forms and Eisenstein series in automorphic representations and string theory applications.
Modular forms Infographic
 libterm.com
libterm.com