Symplectic geometry explores the properties of smooth manifolds equipped with a closed, non-degenerate 2-form, essential for understanding classical and quantum mechanics. This mathematical framework provides powerful tools for analyzing Hamiltonian systems, phase spaces, and conservation laws. Discover how symplectic geometry can deepen your grasp of complex dynamical systems by reading the full article.
Table of Comparison
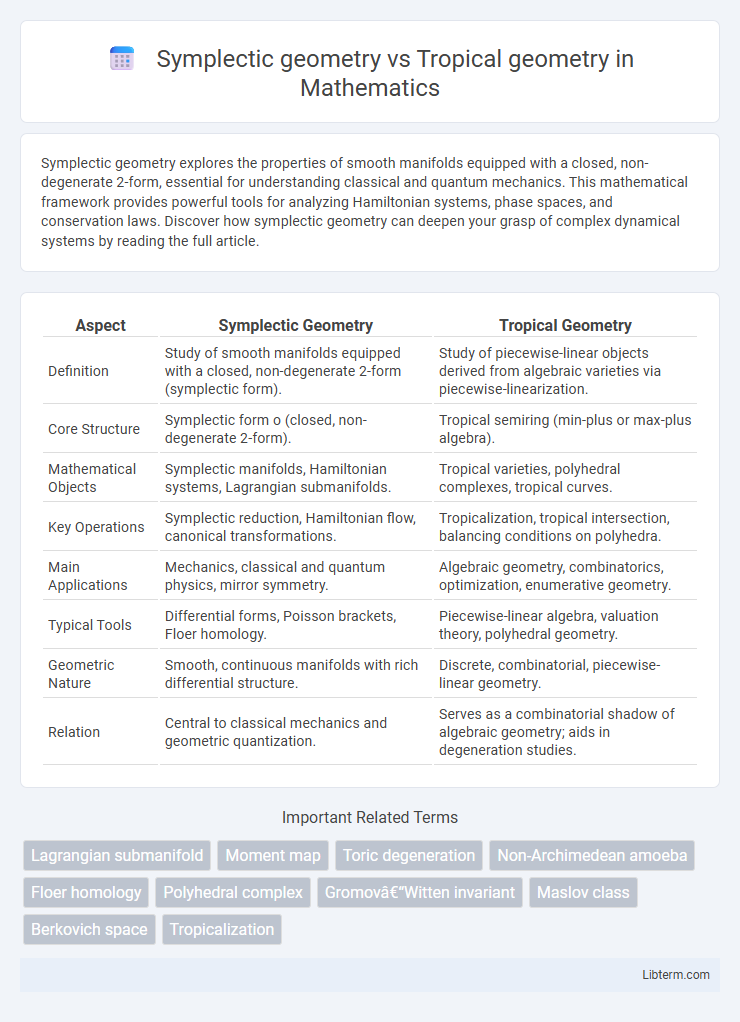
| Aspect | Symplectic Geometry | Tropical Geometry |
|---|---|---|
| Definition | Study of smooth manifolds equipped with a closed, non-degenerate 2-form (symplectic form). | Study of piecewise-linear objects derived from algebraic varieties via piecewise-linearization. |
| Core Structure | Symplectic form o (closed, non-degenerate 2-form). | Tropical semiring (min-plus or max-plus algebra). |
| Mathematical Objects | Symplectic manifolds, Hamiltonian systems, Lagrangian submanifolds. | Tropical varieties, polyhedral complexes, tropical curves. |
| Key Operations | Symplectic reduction, Hamiltonian flow, canonical transformations. | Tropicalization, tropical intersection, balancing conditions on polyhedra. |
| Main Applications | Mechanics, classical and quantum physics, mirror symmetry. | Algebraic geometry, combinatorics, optimization, enumerative geometry. |
| Typical Tools | Differential forms, Poisson brackets, Floer homology. | Piecewise-linear algebra, valuation theory, polyhedral geometry. |
| Geometric Nature | Smooth, continuous manifolds with rich differential structure. | Discrete, combinatorial, piecewise-linear geometry. |
| Relation | Central to classical mechanics and geometric quantization. | Serves as a combinatorial shadow of algebraic geometry; aids in degeneration studies. |
Introduction to Symplectic and Tropical Geometry
Symplectic geometry studies smooth manifolds equipped with a closed, non-degenerate 2-form, central to classical mechanics and Hamiltonian systems. Tropical geometry translates algebraic varieties into piecewise-linear objects using the tropical semiring, facilitating combinatorial approaches to complex problems. Both fields intersect in mirror symmetry and integrable systems, offering complementary perspectives on geometric and algebraic structures.
Historical Development of Both Fields
Symplectic geometry originated in the 20th century with roots tracing back to classical mechanics and the study of Hamiltonian systems, formalized by mathematicians such as Hermann Weyl and Andre Weil. Tropical geometry emerged more recently in the late 20th and early 21st centuries as a combinatorial shadow of algebraic geometry, pioneered by researchers like Imre Simon and Bernd Sturmfels. Both fields have evolved through interdisciplinary collaborations linking mathematics, physics, and computer science, with symplectic geometry emphasizing smooth structures and tropical geometry focusing on piecewise-linear, polyhedral objects.
Key Concepts in Symplectic Geometry
Symplectic geometry centers on the study of symplectic manifolds, which are smooth even-dimensional spaces equipped with a closed, non-degenerate 2-form called the symplectic form, critical for modeling classical mechanics. Key concepts include Hamiltonian systems, moment maps, and Lagrangian submanifolds, which link the geometry to physical dynamics and integrable systems. Unlike tropical geometry, which uses piecewise-linear structures to study degenerations of algebraic varieties, symplectic geometry emphasizes smooth structures and differential forms fundamental to modern mathematical physics.
Fundamental Ideas of Tropical Geometry
Tropical geometry translates classical algebraic varieties into piecewise-linear structures by replacing operations of addition and multiplication with minimum or maximum functions and addition, respectively, forming a tropical semiring. This combinatorial approach captures essential geometric and topological properties, enabling efficient computations and insights into complex algebraic varieties. It contrasts with symplectic geometry, which studies smooth manifolds equipped with a non-degenerate, closed 2-form, focusing on continuous structures and dynamics rather than piecewise-linear combinatorial models.
Analytical Techniques and Tools
Symplectic geometry employs analytical techniques such as Floer homology, Gromov-Witten invariants, and Hamiltonian dynamics to study smooth manifolds equipped with a closed, non-degenerate 2-form, enabling deep insights into the topology and behavior of phase spaces. Tropical geometry utilizes combinatorial and polyhedral methods, relying on piecewise-linear structures and valuations to transform complex algebraic varieties into tropical varieties, facilitating easier computation of intersection numbers and other invariants. Both fields leverage powerful tools like moduli spaces and mirror symmetry frameworks, but symplectic methods emphasize smooth analytical machinery while tropical techniques focus on discrete, combinatorial models.
Intersections and Connections Between the Two Geometries
Symplectic geometry studies smooth manifolds equipped with a closed, non-degenerate 2-form, focusing on structures like Lagrangian submanifolds and their intersections, which play a crucial role in classical and quantum mechanics. Tropical geometry, a piecewise-linear counterpart, translates algebraic varieties into combinatorial polyhedral complexes, allowing for intersection theory via tropical cycles and balancing conditions. Connections between the two arise in mirror symmetry and non-archimedean analytic geometry, where tropical intersections correspond to counts of holomorphic curves in symplectic geometry, revealing deep dualities and computational tools in enumerative geometry.
Applications in Mathematics and Physics
Symplectic geometry plays a crucial role in classical and quantum mechanics, providing a framework for phase space analysis, Hamiltonian dynamics, and integrable systems, while tropical geometry offers combinatorial tools for solving complex enumeration problems, moduli spaces, and mirror symmetry in algebraic geometry. Applications in physics include the use of symplectic structures to study stability and chaos in dynamical systems, whereas tropical geometry aids in understanding string theory compactifications and enumerative invariants through piecewise-linear approximations. Both fields intersect in modern research on mirror symmetry and enumerative geometry, enhancing techniques for solving deep problems in mathematical physics.
Notable Theorems and Results
Symplectic geometry features notable results like Gromov's non-squeezing theorem, which demonstrates rigidity properties of symplectic embeddings, and the Arnold conjecture on fixed points of Hamiltonian diffeomorphisms. Tropical geometry provides the Fundamental Theorem of Tropical Geometry, establishing a link between algebraic varieties and their tropicalizations, alongside the Structure Theorem highlighting polyhedral complexes underlying tropical varieties. Both fields contribute profound theorems connecting algebraic and geometric frameworks, yet symplectic geometry emphasizes smooth and continuous structures, whereas tropical geometry focuses on combinatorial and piecewise-linear aspects.
Current Research Trends and Open Problems
Current research in symplectic geometry explores the interplay between symplectic invariants and mirror symmetry, with emphasis on Floer theory and its applications to low-dimensional topology and string theory. Tropical geometry advances by studying its combinatorial structures to model degeneration of algebraic varieties, focusing on the tropicalization process and connections to moduli spaces. Open problems involve establishing rigorous correspondences between symplectic and tropical geometries, particularly in understanding Lagrangian submanifolds' tropical analogs and enhancing computational methods for enumerative invariants.
Future Directions and Interdisciplinary Potential
Symplectic geometry, with its powerful tools for studying smooth manifolds and Hamiltonian systems, is increasingly intersecting with tropical geometry, which provides combinatorial and piecewise-linear models of algebraic varieties, facilitating novel approaches in enumerative geometry and mirror symmetry. Future research focuses on leveraging tropical techniques to simplify complex symplectic problems, enhancing computational methods and deepening understanding of moduli spaces and integrable systems. This interdisciplinary synergy promises advancements in mathematical physics, optimization algorithms, and string theory, bridging continuous and discrete frameworks for richer geometrical insights.
Symplectic geometry Infographic
 libterm.com
libterm.com