A function is a fundamental concept in mathematics and programming that associates each input with exactly one output, enabling predictable and consistent results. Understanding the properties and applications of functions helps you solve complex problems and develop efficient code. Explore the rest of the article to deepen your knowledge of how functions work and their importance in various fields.
Table of Comparison
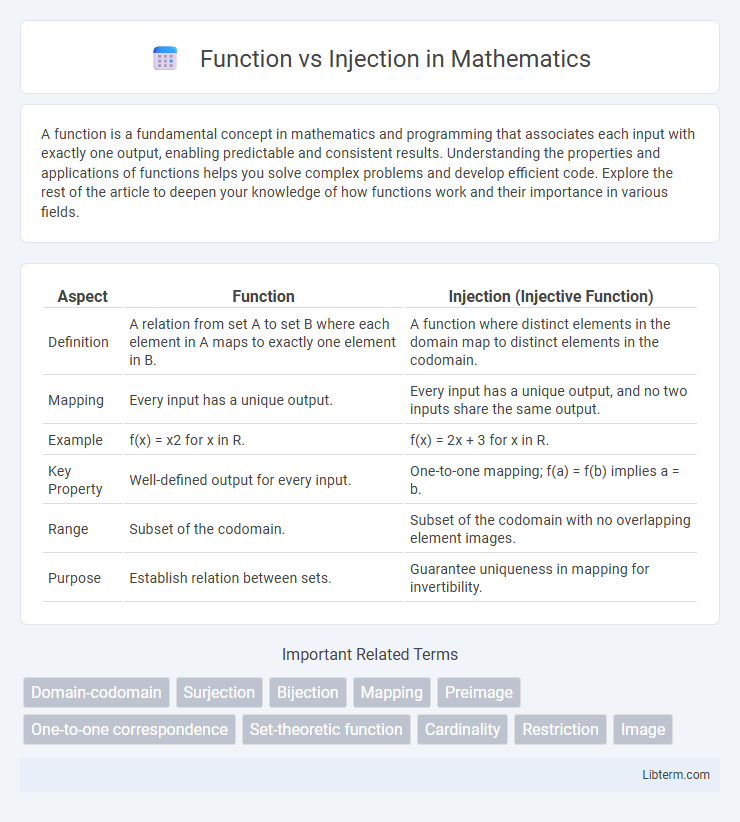
| Aspect | Function | Injection (Injective Function) |
|---|---|---|
| Definition | A relation from set A to set B where each element in A maps to exactly one element in B. | A function where distinct elements in the domain map to distinct elements in the codomain. |
| Mapping | Every input has a unique output. | Every input has a unique output, and no two inputs share the same output. |
| Example | f(x) = x2 for x in R. | f(x) = 2x + 3 for x in R. |
| Key Property | Well-defined output for every input. | One-to-one mapping; f(a) = f(b) implies a = b. |
| Range | Subset of the codomain. | Subset of the codomain with no overlapping element images. |
| Purpose | Establish relation between sets. | Guarantee uniqueness in mapping for invertibility. |
Understanding Function and Injection: Definitions
Functions are reusable blocks of code designed to perform specific tasks and return outputs based on input parameters. Injection refers to the process where external data is inserted into a program, often exploited in security attacks like SQL injection by manipulating input to execute unintended commands. Understanding the definitions of function and injection is essential for developing secure and efficient software systems that prevent vulnerabilities arising from improper input handling.
Key Differences Between Function and Injection
Functions are reusable blocks of code designed to perform specific tasks or calculations, often returning a value after execution. Injection refers to a design pattern primarily used for managing dependencies, where external objects or services are passed into a component to enhance modularity and testability. The key difference lies in functions executing logic or operations, while injection focuses on providing components with necessary resources or dependencies.
Mathematical Background of Functions
Functions in mathematics are defined as mappings from a domain to a codomain, assigning each element exactly one output, highlighting their foundational role in set theory and algebra. Injective functions, or injections, are special mappings where each element in the codomain is mapped by at most one element of the domain, ensuring uniqueness and invertibility on their image. Understanding the distinction between general functions and injections is crucial for analyzing functional behavior, relations, and structures in mathematical contexts such as combinatorics, analysis, and abstract algebra.
Injection: Exploring Injective Functions
Injective functions, also known as one-to-one functions, map each element in the domain to a unique element in the codomain, ensuring no two distinct inputs share the same output. This property is crucial in mathematics and computer science for establishing invertibility and preserving distinctness in transformations. Applications of injective functions include cryptography, data encoding, and establishing isomorphisms in algebraic structures.
Visual Representation: Function vs Injection
Functions in mathematics are often represented visually by graphs where each input corresponds to exactly one output point, ensuring a clear vertical line test. In contrast, injections (injective functions) require that no two distinct inputs map to the same output, visually confirmed if the graph passes the horizontal line test. This distinction is critical when analyzing functions for one-to-one properties and ensures precise understanding through visual inspection.
Real-World Examples of Functions and Injections
Functions map each element of a domain to a unique element in a codomain, exemplified by mathematical operations like squaring a number where each input yields a single output. Injections, a subset of functions, ensure distinct inputs produce distinct outputs, such as assigning unique employee IDs to workers where no two individuals share the same identifier. Real-world applications of injections include database key assignments and user authentication systems, highlighting the importance of one-to-one mappings for data integrity and security.
Identifying Injective Functions: Methods and Tips
Identifying injective functions involves verifying that each element of the function's domain maps to a unique element in the codomain, ensuring one-to-one correspondence. Methods to determine injectivity include the horizontal line test for graphical functions, checking if f(x1) = f(x2) implies x1 = x2 algebraically, and using derivatives to assess monotonicity for continuous functions. Tips include focusing on domain restrictions, analyzing function behavior graphically, and applying inverse function concepts to confirm injectivity precisely.
Role of Injection in Set Theory and Mapping
Injection, also known as an injective function or one-to-one mapping, plays a crucial role in set theory by ensuring that each element of the domain maps to a unique element in the codomain. This property allows injections to establish a correspondence between subsets, preserving distinctness and enabling comparisons of set cardinalities. Unlike general functions, injections prevent overlap in images, which is fundamental for defining embeddings and analyzing structure-preserving maps in mathematical contexts.
Common Misconceptions About Injection and Function
Function and injection are distinct mathematical concepts often confused in set theory and algebra; a function assigns exactly one output to each input, while an injection is a function that never maps distinct inputs to the same output. A common misconception is that all functions are injections, but many functions fail to be injective when two or more elements in the domain share the same image in the codomain. Injection specifically requires a one-to-one mapping, ensuring uniqueness of images, which is not a general requirement for all functions.
Function vs Injection: Summary Table and Quick Reference
The Function vs Injection summary table highlights key distinctions between Function components and Injection patterns in software design, emphasizing their roles, advantages, and typical use cases. Functions encapsulate specific tasks and promote code reusability, while Injection focuses on dependency management and enhances modularity through inversion of control. This quick reference aids developers in selecting the appropriate approach based on maintainability, testability, and system architecture requirements.
Function Infographic
 libterm.com
libterm.com