Primal refers to something fundamental, original, or essential, often connected to natural instincts or basic human nature. Understanding primal behaviors can help you harness innate drives to improve decision-making and personal growth. Explore the rest of this article to discover how primal forces influence your daily life and choices.
Table of Comparison
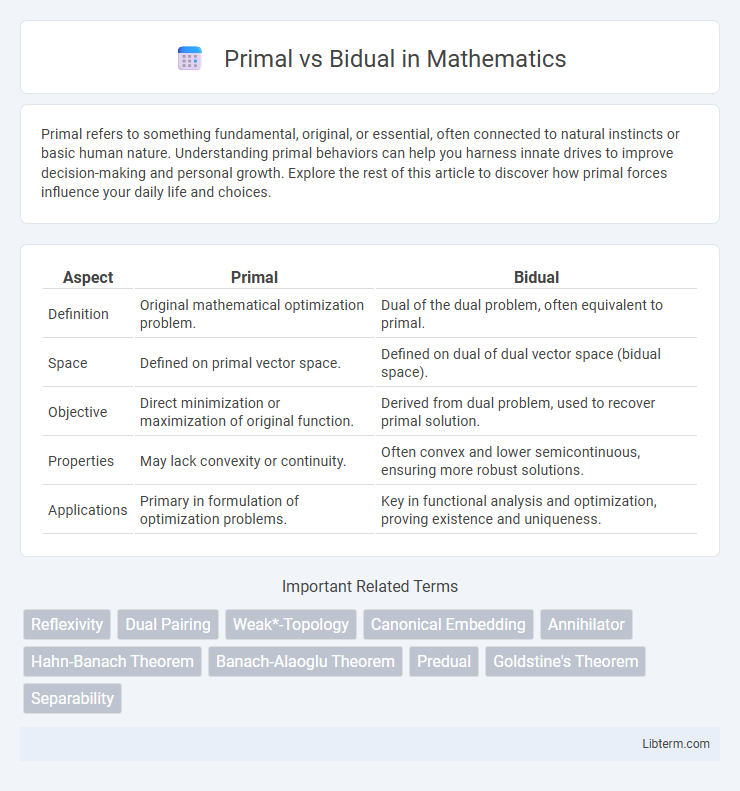
| Aspect | Primal | Bidual |
|---|---|---|
| Definition | Original mathematical optimization problem. | Dual of the dual problem, often equivalent to primal. |
| Space | Defined on primal vector space. | Defined on dual of dual vector space (bidual space). |
| Objective | Direct minimization or maximization of original function. | Derived from dual problem, used to recover primal solution. |
| Properties | May lack convexity or continuity. | Often convex and lower semicontinuous, ensuring more robust solutions. |
| Applications | Primary in formulation of optimization problems. | Key in functional analysis and optimization, proving existence and uniqueness. |
Introduction to Primal and Bidual Concepts
Primal and bidual concepts are fundamental in optimization and functional analysis, involving the relationship between a vector space and its duals. The primal problem refers to the original optimization task defined on a vector space, while the bidual problem leverages the bidual space, often providing a more comprehensive framework for analyzing solution properties. Understanding the bidual space enhances insights into reflexivity, weak* topology, and duality gaps essential in advanced mathematical optimization.
Defining the Primal Space
The primal space is a vector space where original optimization problems are formulated, consisting of variables that directly represent the solution to the problem. Defining the primal space involves specifying the domain and constraints of these variables, ensuring they adhere to the problem's feasibility conditions. This space serves as the foundational framework from which the dual space and bidual concepts are derived, enabling the analysis of optimality and solution properties.
Understanding the Bidual Space
The bidual space of a Banach space X, denoted X, consists of all bounded linear functionals on the dual space X*. Understanding the bidual involves examining the canonical embedding of X into X, which is isometric and linear, allowing every element of X to be represented as a functional on X*. In many cases, X is isometrically isomorphic to a subspace of X, but this embedding may not be surjective, highlighting the distinction between primal and bidual spaces.
Key Differences Between Primal and Bidual
The primal problem in optimization focuses on finding the optimal solution within the original variable space, while the bidual problem is derived from the dual of the dual, often restoring properties of the primal in a different formulation. Key differences include the primal problem being directly related to original constraints, whereas the bidual encapsulates convexification and relaxation effects that may tighten or relax feasibility conditions. The bidual approach often aids in exhibiting strong duality and solution existence under convexity, contrasting the primal's straightforward but sometimes non-convex problem structure.
Importance of Duality in Functional Analysis
Duality in functional analysis provides a fundamental framework for studying vector spaces and their continuous linear functionals, bridging primal and bidual spaces. The primal space captures original function properties, while the bidual, often richer, helps to analyze reflexivity and compactness, crucial in optimization and PDEs. Understanding this relationship enables deeper insights into operator theory and Banach space geometry, facilitating advanced mathematical modeling and problem-solving.
Reflexivity: When Primal Equals Bidual
Reflexivity in functional analysis occurs when a Banach space is isomorphic to its bidual, meaning the natural embedding from the primal space into its bidual is surjective. This property characterizes reflexive spaces, including important examples like Hilbert spaces and \(L^p\) spaces for \(1 < p < \infty\). Reflexivity ensures that the dual of the dual space retains the geometric and topological structure of the original space, enabling powerful applications in optimization and partial differential equations.
Primal and Bidual Applications in Optimization
Primal optimization problems focus on directly minimizing or maximizing an objective function subject to constraints, often solving resource allocation, scheduling, and structural design problems. Bidual approaches involve formulating the dual of the dual problem, enhancing solution robustness and stability in linear, nonlinear, and convex optimization scenarios. Applications in machine learning, network flow, and portfolio optimization leverage both primal and bidual formulations to improve convergence and optimize computational efficiency.
Real-World Examples: Primal vs Bidual
In optimization problems such as resource allocation, the primal formulation directly models the original constraints and objectives, like minimizing production cost by adjusting input quantities. The bidual approach, derived from duality theory, often appears in financial portfolio optimization, where maximizing utility under risk constraints mirrors the primal problem's structure but provides computational advantages. Real-world applications demonstrate that solving the primal problem offers intuitive interpretations, while bidual methods enhance stability and convergence in complex scenarios such as supply chain management and energy systems optimization.
Challenges in Working with Biduals
Challenges in working with biduals include increased complexity due to the bidual space often being larger and less intuitive than the primal space, which complicates analysis and computations. The bidual's topology may differ significantly, leading to difficulties in preserving properties like compactness or reflexivity. Moreover, identifying natural embeddings and interpreting functionals in biduals requires advanced understanding of functional analysis, making practical applications more demanding.
Future Perspectives in Primal and Bidual Research
Future perspectives in primal and bidual research emphasize advancing optimization techniques through enhanced duality theories and novel algorithmic frameworks. Integration of machine learning with primal-dual methods promises improved convergence rates and scalability in large-scale optimization problems. Emerging applications in economics, engineering, and data science highlight the increasing relevance of primal and bidual frameworks for complex decision-making and resource allocation challenges.
Primal Infographic
 libterm.com
libterm.com