A sheaf is a bundle of grain stalks neatly tied together after harvesting, symbolizing abundance and hard work. This traditional agricultural practice helps in drying and storing the grain efficiently, preserving its quality. Discover more about the history, symbolism, and modern uses of sheaves in the rest of the article.
Table of Comparison
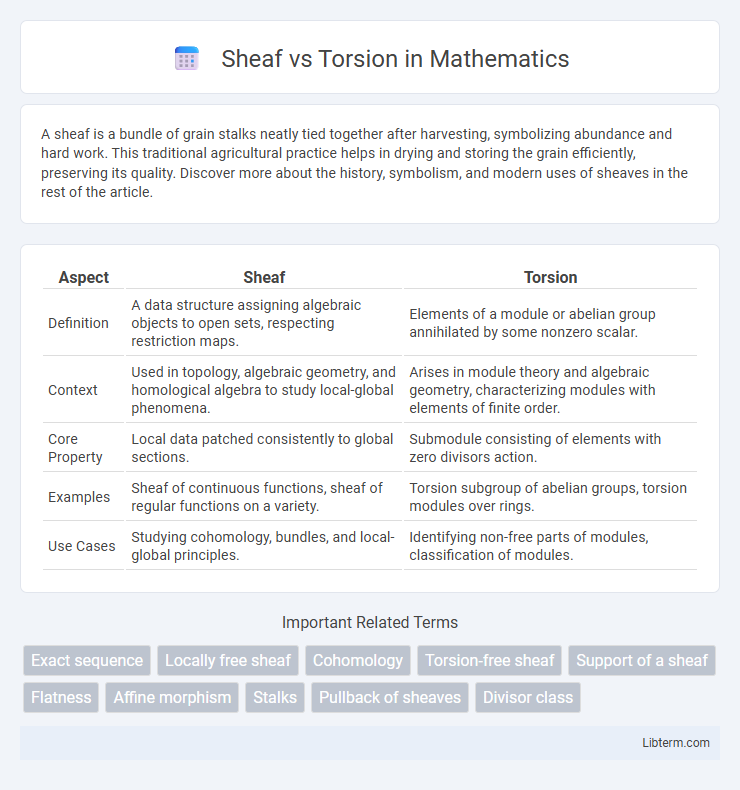
| Aspect | Sheaf | Torsion |
|---|---|---|
| Definition | A data structure assigning algebraic objects to open sets, respecting restriction maps. | Elements of a module or abelian group annihilated by some nonzero scalar. |
| Context | Used in topology, algebraic geometry, and homological algebra to study local-global phenomena. | Arises in module theory and algebraic geometry, characterizing modules with elements of finite order. |
| Core Property | Local data patched consistently to global sections. | Submodule consisting of elements with zero divisors action. |
| Examples | Sheaf of continuous functions, sheaf of regular functions on a variety. | Torsion subgroup of abelian groups, torsion modules over rings. |
| Use Cases | Studying cohomology, bundles, and local-global principles. | Identifying non-free parts of modules, classification of modules. |
Understanding Sheaf: A Foundational Overview
A sheaf systematically organizes local data attached to open subsets of a topological space, enabling their coherent comparison and gluing to form global structures. It generalizes functions, sections, or algebraic objects, serving as a foundational tool in algebraic geometry and topology. Understanding the exactness and stalk behavior of a sheaf is crucial before exploring torsion phenomena, which relate to elements annihilated by nonzero scalars in module sheaves.
What Is Torsion in Mathematical Contexts?
Torsion in mathematical contexts refers to elements of a module or group that have finite order, meaning they are annihilated by some nonzero scalar or integer. In algebraic geometry, torsion sheaves are sheaves supported on subsets where local sections are annihilated by a fixed power of a function, reflecting localized finite order behavior. Understanding torsion is crucial in distinguishing free modules or vector bundles from those with nontrivial torsion components, impacting the structure and classification of sheaves.
Sheaves vs Torsion: Core Differences
Sheaves provide a framework for systematically associating algebraic or topological data to open sets of a space, while torsion refers to elements of a module or group annihilated by nonzero scalars. The core difference lies in their nature: sheaves encapsulate local-to-global data structures and methods, whereas torsion highlights intrinsic algebraic properties related to divisibility and annihilation in modules. Sheaf theory is fundamental in modern algebraic geometry and topology, whereas torsion is a central concept in commutative algebra and group theory.
Key Properties of Sheaves
Sheaves systematically encode local-to-global data by assigning algebraic structures to open sets in a topological space, ensuring consistency through restriction maps and gluing axioms. They are crucial for studying continuous functions, vector bundles, and cohomology theories, enabling precise localization of geometric and algebraic information. In contrast, torsion refers to elements in modules or groups annihilated by nonzero scalars, often analyzed in algebraic topology and homological algebra to detect singularities or obstructions.
Fundamental Characteristics of Torsion
Torsion in algebraic topology and differential geometry is characterized by elements of finite order in a module or homology group, contrasting with sheaves which systematically assign algebraic structures to open sets of a topological space. The fundamental characteristic of torsion is that it measures the obstruction to elements being free or "torsion-free," often detected through torsion submodules or torsion coefficients in homology. This property plays a crucial role in classifying spaces and understanding phenomena such as singularities, where torsion elements reveal subtle geometric and algebraic invariants.
Applications of Sheaves in Modern Mathematics
Sheaves provide a powerful framework in modern mathematics for systematically tracking local data across topological spaces, enabling applications in algebraic geometry, differential geometry, and complex analysis. They are fundamental in the formulation of cohomology theories, allowing mathematicians to study global properties from local conditions. Unlike torsion modules, sheaves capture both algebraic and topological information, making them indispensable in areas such as D-modules, etale cohomology, and the proof of the Weil conjectures.
Role of Torsion in Algebra and Geometry
Torsion plays a crucial role in algebra and geometry by encoding elements of finite order within modules or groups, impacting the structural properties of algebraic objects such as abelian groups and sheaves. In algebraic geometry, torsion sheaves represent phenomena with support on lower-dimensional subsets, effectively capturing local or singular behavior of schemes. This distinction allows torsion elements to serve as essential tools for analyzing geometric invariants and classifying sheaf cohomology.
Sheafification and Torsion Phenomena
Sheafification transforms a presheaf into a sheaf by systematically enforcing locality and gluing conditions, ensuring compatible local data forms a unique global section. Torsion phenomena arise in sheaf theory when sections involve elements annihilated by a nonzero divisor, reflecting intrinsic algebraic obstructions tied to the sheaf's stalks. The interplay between sheafification and torsion highlights how modifying local structures affects global coherence and the detection of torsion elements within the sheaf's module.
Practical Examples: Sheaf and Torsion in Action
Sheaves are crucial in algebraic geometry for systematically tracking local algebraic data, such as sections of a vector bundle, over a topological space, while torsion appears in modules or abelian groups where elements have finite order, impacting the structure of solutions to polynomial equations. A practical example involves coherent sheaves on algebraic curves: torsion sheaves correspond to skyscraper sheaves supported at points, representing singularities or localized phenomena, whereas locally free sheaves correspond to vector bundles describing smooth geometric features. In complex geometry, torsion phenomena influence the classification of sheaves by imposing constraints on extension classes, helping to distinguish between different types of sheaf cohomology that capture geometric invariants.
Sheaf vs Torsion: Summary and Future Directions
Sheaf and torsion are fundamental concepts in algebraic geometry and homological algebra, where sheaves systematically organize local data on topological spaces, while torsion elements in modules reveal obstructions to exactness and provide insight into the structure of abelian groups and sheaf cohomology. Future research focuses on deepening the understanding of torsion phenomena in derived categories and exploring the role of torsion sheaves in moduli problems, enhancing applications in arithmetic geometry and string theory. Advances in computational techniques and categorical frameworks promise to refine the classification of torsion sheaves and their interplay with sheaf cohomology in complex geometric settings.
Sheaf Infographic
 libterm.com
libterm.com