The Levi-Civita symbol is an essential tensor in mathematics and physics used to express permutations and orientations in multidimensional spaces. It plays a crucial role in vector calculus, tensor analysis, and the formulation of physical laws such as electromagnetism and fluid dynamics. Discover how understanding this symbol can enhance your grasp of advanced mathematical concepts by reading the rest of the article.
Table of Comparison
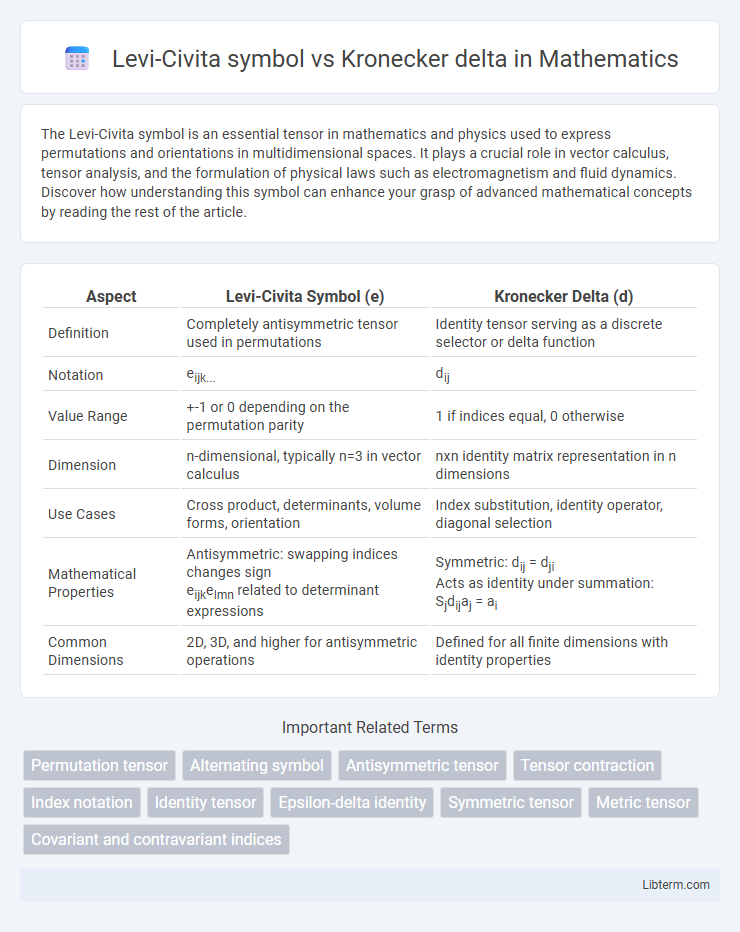
| Aspect | Levi-Civita Symbol (e) | Kronecker Delta (d) |
|---|---|---|
| Definition | Completely antisymmetric tensor used in permutations | Identity tensor serving as a discrete selector or delta function |
| Notation | eijk... | dij |
| Value Range | +-1 or 0 depending on the permutation parity | 1 if indices equal, 0 otherwise |
| Dimension | n-dimensional, typically n=3 in vector calculus | nxn identity matrix representation in n dimensions |
| Use Cases | Cross product, determinants, volume forms, orientation | Index substitution, identity operator, diagonal selection |
| Mathematical Properties |
Antisymmetric: swapping indices changes sign eijkelmn related to determinant expressions |
Symmetric: dij = dji Acts as identity under summation: Sjdijaj = ai |
| Common Dimensions | 2D, 3D, and higher for antisymmetric operations | Defined for all finite dimensions with identity properties |
Introduction to Levi-Civita Symbol and Kronecker Delta
The Levi-Civita symbol, denoted as e_ijk, is an antisymmetric tensor used to express cross products and determinants in three-dimensional space, taking values of +1, -1, or 0 based on the permutation parity of its indices. The Kronecker delta, d_ij, acts as an identity operator in index notation, equaling 1 when indices are equal and 0 otherwise, serving as the discrete analog of the identity matrix. Both symbols are fundamental in tensor calculus and vector algebra, facilitating compact representation of equations involving orthogonal transformations and index contractions.
Mathematical Definitions and Notations
The Levi-Civita symbol \(\varepsilon_{ijk}\) is a completely antisymmetric tensor used to represent the sign of permutations in three dimensions, defined such that \(\varepsilon_{123} = 1\) and changes sign upon swapping any two indices, with zero values if any indices are repeated. The Kronecker delta \(\delta_{ij}\) serves as the identity matrix element in tensor notation, defined as 1 when indices are equal and 0 otherwise, effectively acting as the discrete identity operator in summations. Both symbols are fundamental in tensor calculus, with \(\varepsilon_{ijk}\) enabling cross product representations and \(\delta_{ij}\) facilitating index substitution and simplification in multi-index expressions.
Fundamental Properties and Rules
The Levi-Civita symbol is an antisymmetric tensor used to represent permutations and calculate determinants, characterized by values of +1, -1, or 0 depending on the evenness or oddness of index permutations and zeros for repeated indices. The Kronecker delta functions as an identity matrix element selector, returning 1 when indices are equal and 0 otherwise, thereby serving as a discrete analog of the identity function in tensor algebra. Fundamental rules include the product of Levi-Civita symbols being expressible in terms of Kronecker deltas, enabling simplification of cross products and vector identities in multi-dimensional spaces.
Symmetry and Antisymmetry Explained
The Levi-Civita symbol e_{ijk} is an antisymmetric tensor, changing sign whenever two indices are swapped, which is critical in defining orientations and cross products in three dimensions. In contrast, the Kronecker delta d_{ij} is a symmetric tensor acting as the identity element in index notation, remaining invariant under index exchange. This fundamental difference in symmetry properties underpins their distinct roles in tensor calculus, with the Levi-Civita symbol encoding antisymmetric operations and the Kronecker delta representing symmetric identity mappings.
Index Manipulation: Summation and Contraction
The Levi-Civita symbol e_{ijk} facilitates antisymmetric index manipulation through summation and contraction, enabling tensor operations like cross product representation and determinant evaluation in three dimensions. The Kronecker delta d_{ij} serves as the identity for index substitution during summation, effectively performing index contraction by replacing indices and simplifying tensor expressions. Combining e_{ijk} and d_{ij} allows for converting antisymmetric operations into symmetric forms, streamlining tensor calculus and coordinate transformations in physics and engineering.
Applications in Vector Calculus and Physics
The Levi-Civita symbol is essential in vector calculus for expressing cross products and curls, facilitating operations involving antisymmetric tensors and orientation in three-dimensional space. The Kronecker delta serves as the identity matrix in summation and simplifies tensor index manipulations by acting as a substitution operator in Einstein notation. Both symbols are pivotal in physics, particularly in electromagnetism and fluid dynamics, where they enable compact representation of vector identities and the formulation of physical laws.
Relationship Between Levi-Civita and Kronecker Delta
The Levi-Civita symbol and Kronecker delta are fundamentally connected through tensor identities in vector and tensor calculus. The product of two Levi-Civita symbols can be expressed as a determinant involving Kronecker deltas, revealing the antisymmetric nature of the Levi-Civita symbol and the identity properties of the Kronecker delta. This relationship is essential for simplifying expressions in cross products, determinants, and permutation operations within higher-dimensional spaces.
Common Identities and Useful Formulas
The Levi-Civita symbol e_ijk and the Kronecker delta d_ij are fundamental tensors in vector and tensor calculus, frequently used in manipulating cross products and contractions. Core identities include the contraction e_ijk e_lmn = det(d_il d_im d_in; d_jl d_jm d_jn; d_kl d_km d_kn), which expands to sums of products of Kronecker deltas, enabling simplification of permutation tensors. Useful formulas such as e_ijk e_ijl = 2 d_kl and e_ijk d_jl = e_ilk streamline calculations in three-dimensional Euclidean space, pivotal in electromagnetism, fluid dynamics, and continuum mechanics.
Role in Tensor Analysis and Higher Dimensions
The Levi-Civita symbol serves as an antisymmetric tensor crucial for defining orientations and calculating cross products in three and higher dimensions, enabling the representation of volume and pseudovector operations. In contrast, the Kronecker delta functions as an identity tensor, facilitating index substitution and simplifying expressions through its properties as the discrete identity matrix in any dimension. Both are fundamental in tensor analysis, with the Levi-Civita symbol encoding skew-symmetric operations and the Kronecker delta providing component-wise selection, essential for manipulating and contracting indices in multidimensional tensor calculus.
Practical Examples and Problem-Solving Techniques
The Levi-Civita symbol is essential in vector calculus and physics for expressing cross products and determinants, while the Kronecker delta functions as an identity matrix in summations and index notation. Practical examples include using the Levi-Civita symbol to simplify the curl of a vector field and employing the Kronecker delta to convert between tensor components or to select terms in Einstein summation. Problem-solving techniques often involve leveraging the antisymmetric properties of the Levi-Civita symbol to handle orientation-dependent operations and applying the Kronecker delta to streamline calculations by eliminating index variables.
Levi-Civita symbol Infographic
 libterm.com
libterm.com