Dominating behavior often stems from a desire to control situations or people, reflecting underlying insecurities or a need for power. Recognizing these patterns in yourself or others is crucial for fostering healthier interactions and mutual respect. Explore the rest of this article to understand how you can address and transform dominating tendencies effectively.
Table of Comparison
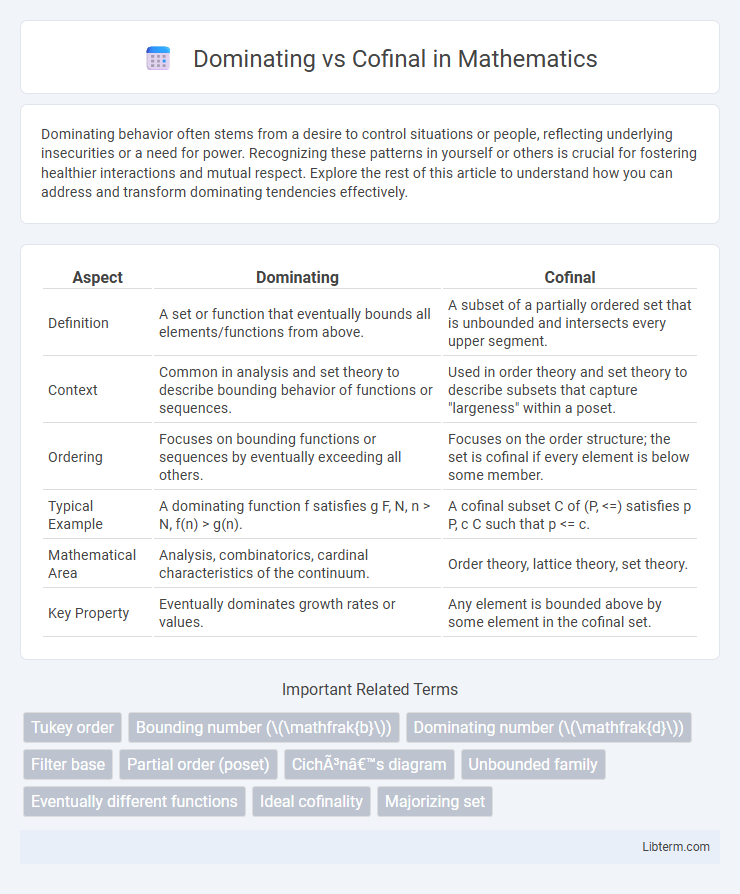
| Aspect | Dominating | Cofinal |
|---|---|---|
| Definition | A set or function that eventually bounds all elements/functions from above. | A subset of a partially ordered set that is unbounded and intersects every upper segment. |
| Context | Common in analysis and set theory to describe bounding behavior of functions or sequences. | Used in order theory and set theory to describe subsets that capture "largeness" within a poset. |
| Ordering | Focuses on bounding functions or sequences by eventually exceeding all others. | Focuses on the order structure; the set is cofinal if every element is below some member. |
| Typical Example | A dominating function f satisfies g F, N, n > N, f(n) > g(n). | A cofinal subset C of (P, <=) satisfies p P, c C such that p <= c. |
| Mathematical Area | Analysis, combinatorics, cardinal characteristics of the continuum. | Order theory, lattice theory, set theory. |
| Key Property | Eventually dominates growth rates or values. | Any element is bounded above by some element in the cofinal set. |
Understanding Dominating and Cofinal Sets
Dominating sets in a partially ordered set (poset) are subsets where every element outside the set is less than or equal to some element inside it, capturing the notion of upper bounds within the structure. Cofinal sets, also known as unbounded sets, are subsets that intersect every upper segment of the poset, ensuring that for every element in the poset, there is a larger or equal element in the cofinal set. Understanding the distinction between dominating and cofinal sets is crucial for analyzing the order-theoretic properties of posets, especially in studying chain conditions and cardinal invariants.
Key Concepts: Order Theory Foundations
Dominating and cofinal subsets are fundamental concepts in order theory, where a dominating subset in a partially ordered set (poset) ensures every element is less than or equal to some element of this subset, establishing an upper bound framework. Cofinal subsets guarantee that for every element in the poset, there exists a larger or equivalent element within the subset, ensuring the poset is "cofinal" with that subset. These concepts underpin the structure of directed sets and nets, playing a critical role in understanding limits, compactness, and completeness in ordered structures.
Formal Definitions of Dominating vs Cofinal
A dominating subset in a partially ordered set is defined such that every element in the set is less than or equal to some element in the dominating subset, ensuring it bounds the set from above. A cofinal subset is characterized by the property that for every element in the partially ordered set, there exists an element in the cofinal subset greater than or equal to it, making it unbounded within the set. Formally, a subset \(D\) of a poset \(P\) is dominating if \(\forall x \in P, \exists d \in D\) with \(x \leq d\), while \(C\) is cofinal in \(P\) if \(\forall x \in P, \exists c \in C\) such that \(x \leq c\).
Examples of Dominating and Cofinal Sets
Dominating sets in a partially ordered set include elements that eventually surpass every other element, such as the set of all functions from natural numbers to natural numbers where each function eventually exceeds any fixed function, illustrating dominance in growth rates. Cofinal sets contain elements that are unbounded above, like the set of all integers greater than a given integer, ensuring every element in the poset is less than or equal to some element in the cofinal set. For example, in the real numbers with the usual order, the set of all numbers greater than zero is cofinal but not dominating, whereas the set of all functions growing faster than any polynomial provides an example of a dominating set in function spaces.
Relationships Between Dominating and Cofinal
Dominating and cofinal sets both describe specific ordering properties in partially ordered sets, where a dominating set intersects every maximal chain and a cofinal set has elements exceeding or equal to any element in the set. A dominating set is always cofinal in a poset because it affects every maximal chain, ensuring coverage beyond all elements' bounds. The relationship highlights that while all dominating sets are cofinal, not every cofinal set dominates maximal chains, focusing on coverage versus intersection in order theory.
Importance in Set Theory and Analysis
Dominating and cofinal sets play crucial roles in set theory and real analysis by structuring order types and guiding convergence behavior. A dominating family in the context of functions often describes a set that eventually exceeds every function from a smaller family, impacting cardinal characteristics of the continuum. Cofinal subsets ensure that every element in a partially ordered set is bounded above, which is vital for understanding chains, limits, and ordinal cofinality in both theoretical and applied analysis.
Applications in Infinite Ordered Structures
Dominating and cofinal subsets play crucial roles in the analysis of infinite ordered structures, particularly within set theory and model theory. Dominating sets help characterize functions that eventually exceed all others in a given order, facilitating the classification of order types and growth rates in omega-sequences. Cofinal subsets ensure unboundedness in partially ordered sets, enabling the construction of limits, filters, and ultrafilters essential for advanced applications like forcing and large cardinal theories.
Dominating vs Cofinal in Function Spaces
In function spaces, a dominating family is a set of functions \( \mathcal{D} \subseteq \omega^\omega \) such that every function \( f \in \omega^\omega \) is eventually bounded by some \( d \in \mathcal{D} \), meaning \( f(n) \leq d(n) \) for all sufficiently large \( n \). A cofinal family in the same space is a subset \( \mathcal{C} \subseteq \omega^\omega \) where for every \( f \in \omega^\omega \), there exists \( c \in \mathcal{C} \) with \( f \leq c \) pointwise or with respect to some ordering, implying \( \mathcal{C} \) is unbounded and captures supremum behavior. The key difference lies in dominating families imposing eventual bounds versus cofinal families achieving unboundedness or supremum coverage in the partial order of functions.
Cardinalities: Dominating and Cofinal Numbers
Dominating and cofinal numbers are key concepts in set theory related to cardinalities. A dominating number, denoted by \( \mathfrak{d} \), is the smallest cardinality of a family of functions from \(\omega\) to \(\omega\) such that every function is eventually dominated by some function in the family. The cofinal number, denoted by \( \mathrm{cf}(\kappa) \) for a cardinal \(\kappa\), is the smallest cardinality of a cofinal subset in \(\kappa\), reflecting the minimal size needed to "reach" \(\kappa\) through an unbounded ascending chain.
Open Questions and Research Directions
Open questions in dominating versus cofinal structures center on characterizing minimal dominating sets and their relationship to cofinal subsets in various partially ordered sets. Research directions involve exploring the computational complexity of identifying dominating versus cofinal elements and understanding their interplay in infinite combinatorics and lattice theory. Advances in this area could reveal new insights into order types, fixed point properties, and applications in algorithm design.
Dominating Infographic
 libterm.com
libterm.com