The gamma function extends the factorial function to complex and real number arguments, providing a continuous interpolation for factorial values beyond integers. It plays a crucial role in various fields such as calculus, probability theory, and complex analysis due to its unique properties and applications. Explore the rest of this article to deepen your understanding of the gamma function's significance and practical uses.
Table of Comparison
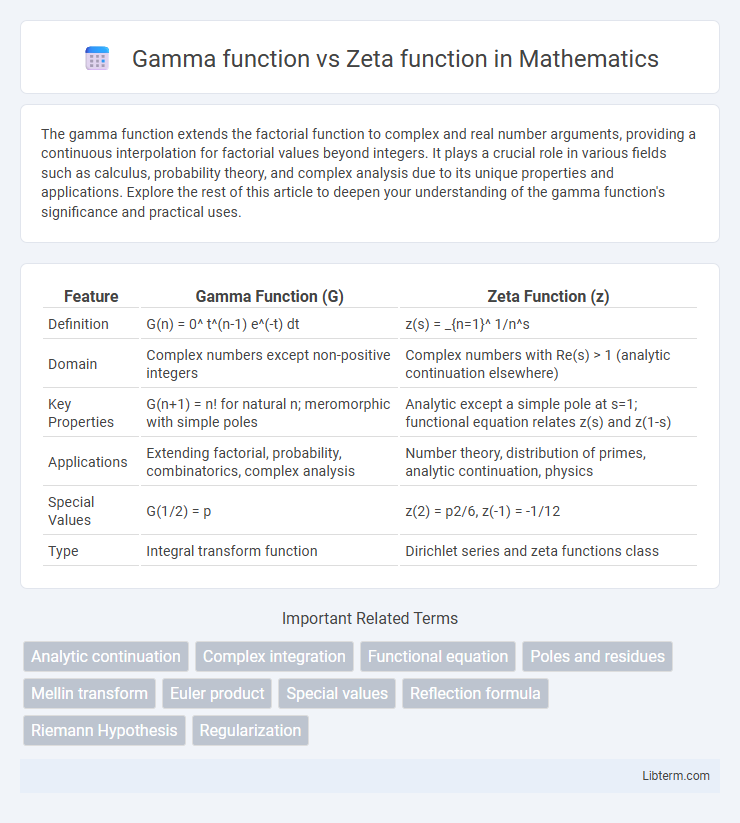
| Feature | Gamma Function (G) | Zeta Function (z) |
|---|---|---|
| Definition | G(n) = 0^ t^(n-1) e^(-t) dt | z(s) = _{n=1}^ 1/n^s |
| Domain | Complex numbers except non-positive integers | Complex numbers with Re(s) > 1 (analytic continuation elsewhere) |
| Key Properties | G(n+1) = n! for natural n; meromorphic with simple poles | Analytic except a simple pole at s=1; functional equation relates z(s) and z(1-s) |
| Applications | Extending factorial, probability, combinatorics, complex analysis | Number theory, distribution of primes, analytic continuation, physics |
| Special Values | G(1/2) = p | z(2) = p2/6, z(-1) = -1/12 |
| Type | Integral transform function | Dirichlet series and zeta functions class |
Introduction to Special Functions
The Gamma function extends the factorial function to complex and real number arguments, defined through an improper integral that converges for positive real parts of the input. The Riemann Zeta function, a fundamental object in analytic number theory, is defined as a series summation over positive integers raised to a complex power and extended via analytic continuation. Both functions are crucial special functions in mathematics, with applications spanning complex analysis, number theory, and physics, often interconnected through integral transforms and functional equations.
Definition of the Gamma Function
The Gamma function, denoted as G(n), is a continuous extension of the factorial function to complex and real number arguments, defined by the improper integral G(z) = 0^ t^(z-1) e^(-t) dt for complex numbers with a positive real part. Unlike the Zeta function, which is primarily a series used in number theory and defined by z(s) = n=1^ 1/n^s for Re(s) > 1, the Gamma function is crucial in complex analysis, probability theory, and combinatorics due to its role in integral transforms and special functions. Both functions exhibit deep connections in analytic number theory but serve different purposes: the Gamma function generalizes factorials while the Zeta function encodes properties of prime numbers through its zeros.
Definition of the Zeta Function
The Zeta function, specifically the Riemann Zeta function z(s), is defined as the infinite series sum of 1/n^s for complex variable s with real part greater than 1, and it can be analytically continued to other values except s=1. Unlike the Gamma function, which generalizes factorials through an integral representation, the Zeta function encodes deep properties of prime numbers via its Euler product formula. Its values and zeros play a crucial role in number theory and the distribution of prime numbers.
Historical Background and Origins
The Gamma function, introduced by Leonhard Euler in the 18th century, extends the factorial function to complex numbers and played a crucial role in the development of complex analysis and calculus. The Zeta function, primarily associated with Bernhard Riemann in the 19th century, originated from Leonhard Euler's earlier work on series and products, serving as a fundamental object in number theory and the study of prime distribution. Both functions have deep historical roots, with Euler's groundbreaking insights laying the foundation for Riemann's advances in analytic number theory.
Analytical Properties: Poles and Singularities
The Gamma function, defined for complex numbers except at non-positive integers, exhibits simple poles at these negative integers and zero, with residues related to factorial values. In contrast, the Riemann Zeta function has a simple pole at s = 1 with residue 1, while being analytic elsewhere in the complex plane except for trivial zeros at negative even integers. Both functions play crucial roles in complex analysis through their distinct singularity structures, influencing their applications in number theory and mathematical physics.
Functional Equations and Reflection Formulas
The Gamma function satisfies the functional equation G(z+1) = zG(z), which extends the factorial to complex numbers, and its reflection formula G(z)G(1-z) = p/sin(pz) relates values at z and 1-z. The Riemann zeta function follows the functional equation z(1-s) = 2(2p)^(-s)cos(ps/2)G(s)z(s), connecting values at s and 1-s. These reflection formulas reveal deep symmetries and analytic continuations essential for complex analysis and number theory.
Roles in Complex Analysis
The Gamma function extends factorial operations to complex numbers, playing a fundamental role in complex analysis through analytic continuation and residue calculus. The Riemann Zeta function, central in number theory and complex analysis, encodes distribution of prime numbers via its nontrivial zeros and exhibits deep connections to the critical line and functional equations. Both functions underpin significant theorems and techniques in evaluating complex integrals, asymptotic expansions, and the study of special functions.
Applications in Number Theory and Physics
The Gamma function plays a crucial role in number theory by generalizing factorials and enabling the extension of combinatorial identities to complex numbers, while its connection to the Beta function aids in the evaluation of integrals and series. The Zeta function, particularly the Riemann Zeta function, is central to analytic number theory, facilitating the study of prime number distribution through its non-trivial zeros. In physics, the Gamma function appears in quantum mechanics and statistical mechanics for computations involving factorials of non-integers, whereas the Zeta function proves essential in quantum field theory and thermodynamics, especially in regularizing divergent series and analyzing spectral properties.
Key Differences Between Gamma and Zeta Functions
The Gamma function generalizes the factorial function to complex numbers, defined by an integral representation convergent for positive real parts, while the Zeta function, notably the Riemann Zeta function, is a complex function crucial in number theory and analytic continuation with a series definition convergent for real parts greater than one. The Gamma function appears primarily in probability theory, combinatorics, and complex analysis, whereas the Zeta function is pivotal in studying the distribution of prime numbers and has profound implications in the Riemann Hypothesis. Unlike the Gamma function, which lacks zeros and has simple poles at non-positive integers, the Zeta function has both trivial zeros at negative even integers and nontrivial zeros in the critical strip, deeply influencing the field of analytic number theory.
Conclusion: Comparative Significance
The Gamma function extends factorial concepts to complex numbers, providing essential tools for calculus, complex analysis, and probability theory. The Zeta function, particularly the Riemann Zeta function, plays a crucial role in number theory and the distribution of prime numbers, influencing unsolved problems like the Riemann Hypothesis. Together, these functions underpin fundamental advances in mathematical analysis and theoretical research, each addressing distinct yet complementary aspects of mathematical theory.
Gamma function Infographic
 libterm.com
libterm.com