Diagonalization is a mathematical process used to simplify matrices by transforming them into a diagonal form, making complex calculations more manageable. Understanding how to diagonalize matrices can significantly enhance your problem-solving efficiency in linear algebra and its applications. Explore the rest of the article to master the techniques and benefits of diagonalization.
Table of Comparison
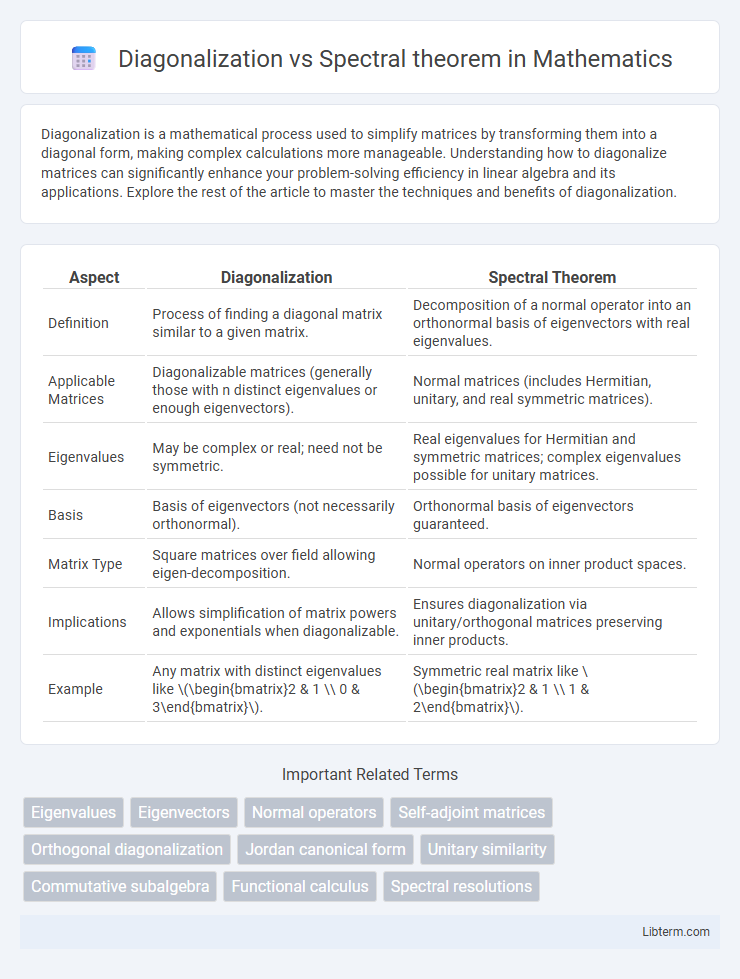
| Aspect | Diagonalization | Spectral Theorem |
|---|---|---|
| Definition | Process of finding a diagonal matrix similar to a given matrix. | Decomposition of a normal operator into an orthonormal basis of eigenvectors with real eigenvalues. |
| Applicable Matrices | Diagonalizable matrices (generally those with n distinct eigenvalues or enough eigenvectors). | Normal matrices (includes Hermitian, unitary, and real symmetric matrices). |
| Eigenvalues | May be complex or real; need not be symmetric. | Real eigenvalues for Hermitian and symmetric matrices; complex eigenvalues possible for unitary matrices. |
| Basis | Basis of eigenvectors (not necessarily orthonormal). | Orthonormal basis of eigenvectors guaranteed. |
| Matrix Type | Square matrices over field allowing eigen-decomposition. | Normal operators on inner product spaces. |
| Implications | Allows simplification of matrix powers and exponentials when diagonalizable. | Ensures diagonalization via unitary/orthogonal matrices preserving inner products. |
| Example | Any matrix with distinct eigenvalues like \(\begin{bmatrix}2 & 1 \\ 0 & 3\end{bmatrix}\). | Symmetric real matrix like \(\begin{bmatrix}2 & 1 \\ 1 & 2\end{bmatrix}\). |
Introduction to Diagonalization and the Spectral Theorem
Diagonalization is the process of finding a diagonal matrix similar to a given square matrix, enabling simplified matrix computations and insight into eigenvalues. The Spectral Theorem states that every normal matrix over the complex field can be diagonalized by a unitary matrix, guaranteeing orthonormal eigenvectors. These concepts establish foundational tools in linear algebra for understanding matrix structure and spectral properties.
Fundamental Concepts: Eigenvalues and Eigenvectors
Eigenvalues represent scalar values associated with a linear transformation, indicating how vectors are scaled during the transformation, while eigenvectors are the non-zero vectors that only change by this scaling factor. Diagonalization involves expressing a matrix as a product of its eigenvectors and a diagonal matrix of eigenvalues, simplifying matrix operations and revealing intrinsic matrix properties. The Spectral Theorem further refines this by guaranteeing diagonalization via an orthonormal basis of eigenvectors for symmetric or normal matrices, emphasizing the fundamental role of eigenvalues and eigenvectors in matrix decomposition.
What is Matrix Diagonalization?
Matrix diagonalization is the process of transforming a square matrix into a diagonal matrix through a similarity transformation involving its eigenvalues and eigenvectors. This transformation simplifies matrix operations by representing the matrix in a basis where it acts as a scaling operator. Unlike the spectral theorem, which applies specifically to normal matrices and guarantees an orthonormal eigenbasis, diagonalization can apply to a broader class of matrices but may not yield orthogonal eigenvectors.
Understanding the Spectral Theorem
The Spectral Theorem provides a comprehensive framework for diagonalizing normal operators on finite-dimensional inner product spaces, ensuring the existence of an orthonormal basis consisting of eigenvectors. Unlike basic diagonalization, which applies to diagonalizable matrices, the Spectral Theorem guarantees a unitary diagonalization for normal matrices, including self-adjoint and unitary operators. This theorem is essential for simplifying operators in quantum mechanics and functional analysis by revealing their spectral decomposition explicitly.
Conditions for Diagonalizability
A matrix is diagonalizable if it has enough linearly independent eigenvectors to form a basis of the vector space, typically requiring distinct eigenvalues or a full set of eigenvectors for repeated eigenvalues. The Spectral Theorem guarantees diagonalizability for normal matrices, such as Hermitian or unitary matrices, by providing an orthonormal eigenbasis and real eigenvalues in the Hermitian case. Non-normal matrices may be diagonalizable, but diagonalization is not assured without meeting the eigenvector completeness condition or similarity to a diagonal matrix.
Spectral Theorem: Applicability and Scope
The Spectral Theorem applies specifically to normal operators on finite-dimensional inner product spaces, ensuring that these operators can be diagonalized via an orthonormal basis of eigenvectors. Unlike general diagonalization, which requires only diagonalizable matrices, the Spectral Theorem guarantees a decomposition with orthogonal projections and real eigenvalues for self-adjoint operators and unitary operators for complex spaces. This makes the Spectral Theorem a powerful tool in functional analysis and quantum mechanics where orthogonality and completeness are essential.
Diagonalization vs Spectral Theorem: Key Differences
Diagonalization applies to matrices that have a full set of linearly independent eigenvectors, allowing them to be expressed as PDP-1, where P is the eigenvector matrix and D is diagonal. The Spectral Theorem specifically applies to normal matrices (including symmetric and Hermitian matrices), ensuring they can be diagonalized via a unitary transformation and that their eigenvalues are real. Unlike general diagonalization, the Spectral Theorem guarantees orthonormal eigenvectors and real eigenvalues, providing a stronger structural guarantee for matrix decomposition.
Practical Applications in Mathematics and Physics
Diagonalization simplifies matrix computations by transforming matrices into diagonal form, facilitating efficient calculation of powers and exponentials crucial in solving linear differential equations and stability analysis in engineering. The Spectral Theorem extends diagonalization to normal operators on inner product spaces, ensuring orthonormal eigenbases in quantum mechanics for observable measurements and vibration analysis in mechanical systems. These concepts enable practical problem-solving in areas such as quantum state evolution, signal processing, and control theory by providing computationally tractable frameworks.
Limitations of Diagonalization and the Spectral Theorem
Diagonalization is limited to square matrices with a full set of linearly independent eigenvectors, excluding defective or non-diagonalizable matrices, while the Spectral Theorem applies specifically to normal operators on finite-dimensional inner product spaces, ensuring diagonalizability via an orthonormal basis. The Spectral Theorem guarantees a unitary diagonalization for Hermitian or normal matrices, but fails for non-normal matrices where eigenvalues may not be sufficient to describe the operator fully. Both approaches do not extend straightforwardly to infinite-dimensional or non-normal operators, restricting their applicability in more general operator theory contexts.
Conclusion: Choosing the Right Approach
Choosing between diagonalization and the spectral theorem depends on the matrix type and its properties; diagonalization applies broadly to matrices with a complete set of eigenvectors, while the spectral theorem specifically addresses normal or symmetric matrices with orthonormal eigenbases. For symmetric or Hermitian matrices, the spectral theorem guarantees real eigenvalues and a diagonal form via a unitary transformation, making it the preferred approach. In contrast, for general diagonalizable matrices, straightforward diagonalization suffices but may not yield orthonormal eigenvectors or real eigenvalues.
Diagonalization Infographic
 libterm.com
libterm.com