Hausdorff measure generalizes the concept of length, area, and volume to irregular and fractal sets, providing a crucial tool in geometric measure theory. It assigns a measure to subsets in metric spaces based on their dimensional properties, often revealing intricate structures that conventional measures overlook. Explore the rest of this article to understand how Hausdorff measure applies to your analysis of complex shapes and dimensions.
Table of Comparison
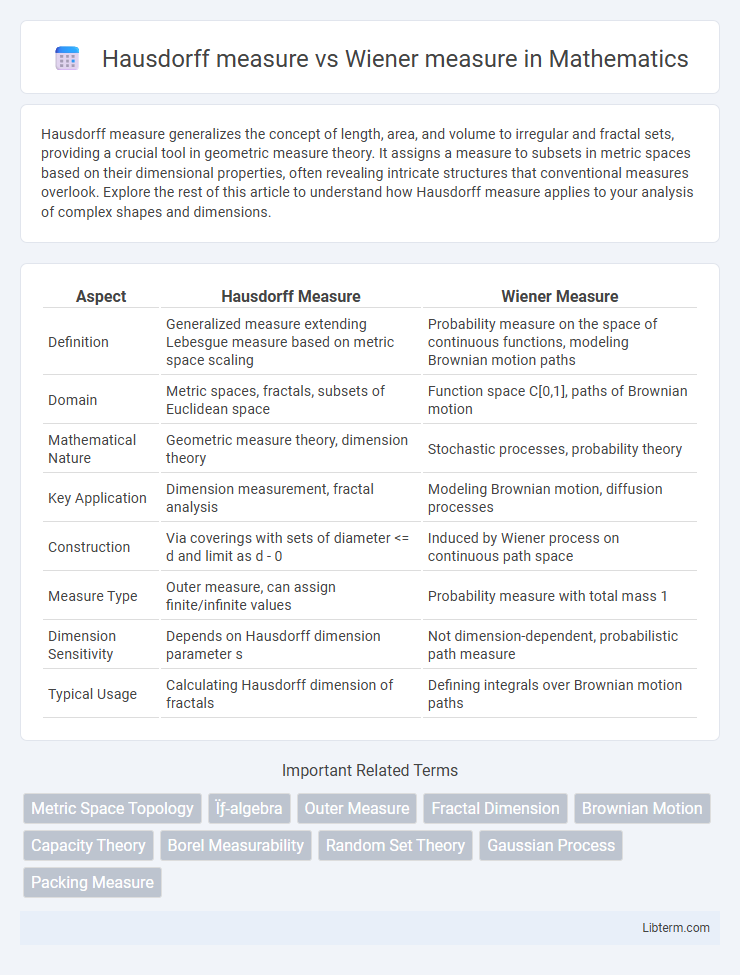
| Aspect | Hausdorff Measure | Wiener Measure |
|---|---|---|
| Definition | Generalized measure extending Lebesgue measure based on metric space scaling | Probability measure on the space of continuous functions, modeling Brownian motion paths |
| Domain | Metric spaces, fractals, subsets of Euclidean space | Function space C[0,1], paths of Brownian motion |
| Mathematical Nature | Geometric measure theory, dimension theory | Stochastic processes, probability theory |
| Key Application | Dimension measurement, fractal analysis | Modeling Brownian motion, diffusion processes |
| Construction | Via coverings with sets of diameter <= d and limit as d - 0 | Induced by Wiener process on continuous path space |
| Measure Type | Outer measure, can assign finite/infinite values | Probability measure with total mass 1 |
| Dimension Sensitivity | Depends on Hausdorff dimension parameter s | Not dimension-dependent, probabilistic path measure |
| Typical Usage | Calculating Hausdorff dimension of fractals | Defining integrals over Brownian motion paths |
Introduction to Hausdorff and Wiener Measures
Hausdorff measure generalizes the concept of length, area, and volume by measuring subsets of metric spaces with varying dimensional scales, making it a crucial tool in fractal geometry and geometric measure theory. Wiener measure, defined on the space of continuous functions, is fundamental in probability theory for modeling Brownian motion and stochastic processes. Understanding the foundational definitions and properties of both measures provides essential insights into geometric analysis and the probabilistic behavior of random paths.
Fundamental Concepts in Measure Theory
Hausdorff measure generalizes Lebesgue measure by assigning measures to subsets of metric spaces using a dimension parameter, capturing fractal geometry through coverings with arbitrarily small sets. Wiener measure, a probability measure on the space of continuous paths, is fundamental in stochastic analysis, describing the distribution of Brownian motion. Both measures exemplify key concepts in measure theory: outer measures, sigma-algebras, and Caratheodory's extension theorem, but differ in application--Hausdorff measure focuses on geometric measure theory, while Wiener measure applies to probabilistic path spaces.
Definition and Construction of the Hausdorff Measure
The Hausdorff measure is defined through a process of covering a set with countably many subsets of arbitrarily small diameter and summing the diameters raised to a fixed power, allowing measurement of fractal dimensions. Constructed via the Caratheodory method, it generalizes the notion of length, area, and volume by adjusting the dimensional parameter to capture complex geometric structures. In contrast, the Wiener measure is a probability measure on path spaces, primarily used in stochastic analysis and Brownian motion, focusing on random continuous functions rather than spatial coverings.
Definition and Construction of the Wiener Measure
The Wiener measure is a probability measure on the space of continuous functions, constructed to model Brownian motion paths, and is defined via the distribution of increments as independent Gaussian random variables with mean zero and variance proportional to the time difference. In contrast, the Hausdorff measure generalizes the concept of Lebesgue measure to fractal and irregular sets by employing a dimension parameter and scaling function to measure subsets of metric spaces. The Wiener measure arises through the use of cylinder sets and consistent finite-dimensional distributions, extending these via Kolmogorov's extension theorem to a complete measure on the path space.
Key Differences Between Hausdorff and Wiener Measures
Hausdorff measure quantifies the size of fractal sets by generalizing length, area, and volume through a dimensional parameter, while Wiener measure defines a probability measure on the space of continuous paths, crucial for modeling Brownian motion. Hausdorff measure is deterministic and geometric, used primarily in fractal geometry and metric spaces, whereas Wiener measure is stochastic, applied in probability theory and stochastic processes. The key difference lies in their domains and purposes: Hausdorff measure assesses fractal dimension and geometric size, whereas Wiener measure governs the distribution of random continuous trajectories.
Applications of Hausdorff Measure in Mathematics
Hausdorff measure plays a crucial role in fractal geometry, enabling precise quantification of sets with non-integer dimensions, such as Cantor sets and Julia sets, which traditional measures cannot capture. It is extensively applied in geometric measure theory to analyze the size and structure of irregular and fractal sets, facilitating advances in harmonic analysis and dynamical systems. These applications contrast with Wiener measure, primarily used in probability theory to model Brownian motion paths and stochastic processes.
Applications of Wiener Measure in Probability Theory
Wiener measure is fundamental in probability theory for modeling Brownian motion as a continuous-time stochastic process, playing a crucial role in stochastic calculus, financial mathematics, and diffusion processes. Unlike the Hausdorff measure, which is primarily a tool in geometric measure theory for assessing fractal dimensions and irregular sets, Wiener measure provides a rigorous probabilistic framework that allows for the construction and analysis of path spaces with properties such as almost sure continuity. Applications of Wiener measure include solving stochastic differential equations, option pricing in mathematical finance, and the study of heat equations via probabilistic methods.
Geometric vs. Probabilistic Interpretations
Hausdorff measure quantifies the size and dimensionality of fractal and irregular geometric sets by generalizing concepts of length, area, and volume in metric spaces. Wiener measure, rooted in probability theory, characterizes the distribution of continuous Brownian paths, enabling probabilistic analysis of random motion in function spaces. The geometric interpretation of Hausdorff measure contrasts with the stochastic interpretation of Wiener measure, highlighting their roles in metric geometry and path-space probability, respectively.
Interactions and Connections Between the Two Measures
Hausdorff measure and Wiener measure interact significantly in the study of fractal geometry and stochastic processes, particularly in understanding path properties of Brownian motion. The Hausdorff measure quantifies the fractal dimension of sets visited by Wiener measure-driven Brownian paths, revealing the intricate geometric structure underlying random motion. Connections between these measures enable precise characterization of hitting probabilities and sample path regularity in probabilistic potential theory.
Conclusion: Choosing the Right Measure for Mathematical Problems
Hausdorff measure excels in analyzing fractal geometry and sets with complex dimensional properties, providing precise scaling and dimensional classification, while Wiener measure is essential in modeling stochastic processes like Brownian motion, offering a probabilistic framework for path spaces. Selecting the appropriate measure depends on the problem's core focus: use Hausdorff measure for geometric measure theory and fractal analysis, and Wiener measure for probabilistic modeling in continuous-time stochastic analysis. Understanding the distinct roles and applications ensures accurate mathematical modeling and effective problem-solving in both deterministic geometry and random process contexts.
Hausdorff measure Infographic
 libterm.com
libterm.com