Monomorphism refers to a concept in mathematics and computer science where a function, operation, or structure is defined with a single, uniform type or form. This property ensures consistency and predictability in how data or objects are manipulated within a system. Explore the rest of the article to understand how monomorphism simplifies complex problems and enhances your computational designs.
Table of Comparison
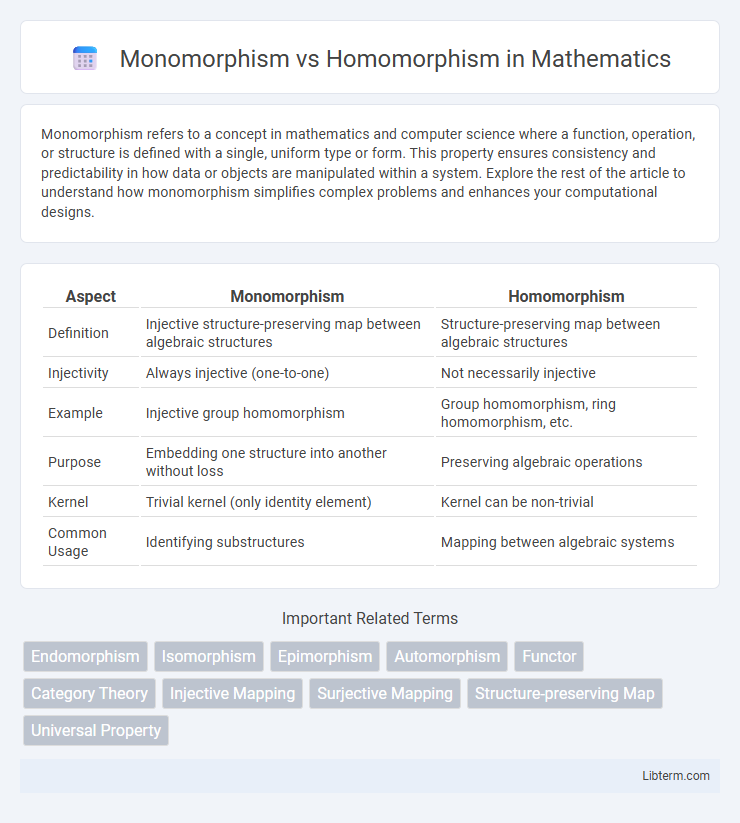
| Aspect | Monomorphism | Homomorphism |
|---|---|---|
| Definition | Injective structure-preserving map between algebraic structures | Structure-preserving map between algebraic structures |
| Injectivity | Always injective (one-to-one) | Not necessarily injective |
| Example | Injective group homomorphism | Group homomorphism, ring homomorphism, etc. |
| Purpose | Embedding one structure into another without loss | Preserving algebraic operations |
| Kernel | Trivial kernel (only identity element) | Kernel can be non-trivial |
| Common Usage | Identifying substructures | Mapping between algebraic systems |
Introduction to Monomorphism and Homomorphism
Monomorphism and homomorphism are fundamental concepts in algebra that describe structure-preserving maps between algebraic structures. A monomorphism is an injective homomorphism that embeds one structure into another without collapsing distinct elements, ensuring a one-to-one correspondence within the mapping. Homomorphisms, more generally, are functions between two algebraic structures, such as groups, rings, or vector spaces, that preserve operations like addition or multiplication, enabling an analysis of their structural similarities.
Defining Monomorphism
Monomorphism is a morphism in category theory that is injective, meaning it preserves distinctness by mapping different elements in the domain to different elements in the codomain. It is a structure-preserving map that is left-cancellable, ensuring that if two morphisms composed with a monomorphism are equal, then those two morphisms themselves must be equal. This property makes monomorphisms analogous to injective functions in the category of sets, serving as a foundation for understanding object embeddings within various mathematical structures.
Defining Homomorphism
Homomorphism is a structure-preserving map between two algebraic structures, such as groups, rings, or vector spaces, that respects the operations defined on those structures. It ensures that the image of a combined operation in the domain corresponds exactly to the combined operation of the images in the codomain, maintaining algebraic consistency. This contrasts with monomorphisms, which are injective homomorphisms emphasizing one-to-one mappings while still preserving the underlying structure.
Key Differences Between Monomorphism and Homomorphism
Monomorphism is an injective structure-preserving map between algebraic structures, ensuring distinct elements are mapped to distinct elements, while homomorphism is a general structure-preserving function that may not be injective or surjective. The key difference lies in monomorphisms being injective homomorphisms that maintain one-to-one correspondence, whereas homomorphisms only preserve operations without the injectivity condition. Monomorphisms allow embedding substructures within larger structures, but homomorphisms enable more general mappings that may identify or collapse elements.
Mathematical Contexts: Monomorphism vs Homomorphism
In mathematical contexts, a monomorphism is an injective homomorphism that preserves structure and ensures distinct elements map to distinct elements, often used in categories like groups or modules. Homomorphisms are general structure-preserving maps between algebraic structures such as groups, rings, or vector spaces, without necessarily being injective. The key difference lies in monomorphisms requiring injectivity, making them embeddings that reflect the source's structure faithfully within the target.
Examples and Applications of Monomorphisms
Monomorphisms appear frequently in category theory and algebra, such as injective functions in set theory or inclusion maps in group theory, where they preserve structure by embedding one object into another without loss of information. Examples include the inclusion of a subgroup \(H\) into a group \(G\) or the injection of a vector subspace into a vector space, both serving critical roles in defining substructures and embeddings. Applications of monomorphisms extend to computer science in type theory for ensuring type safety and in database schema design for enforcing entity integrity constraints.
Examples and Applications of Homomorphisms
Homomorphisms map algebraic structures like groups, rings, and vector spaces while preserving operations, such as addition or multiplication; for example, the function f(x) = 2x from integers under addition to even integers is a group homomorphism. Applications of homomorphisms include simplifying complex algebraic problems by studying their structural images, enabling cryptographic protocols like RSA to operate securely through ring homomorphisms, and encoding data in error-correcting codes where homomorphisms maintain linear structure in vector spaces. Unlike monomorphisms, which are injective homomorphisms preserving structure without collapsing information, general homomorphisms allow many-to-one mappings critical in abstract algebra and computer science.
Visualizing Monomorphism and Homomorphism
Visualizing monomorphisms involves identifying injective structure-preserving maps that embed one algebraic structure into another without loss of information, often depicted as arrows with a hooked tail in category theory diagrams. Homomorphisms are represented as arrows showing general structure-preserving functions between algebraic objects, where the focus is on maintaining operation compatibility rather than injectivity. Diagrammatic interpretations of monomorphisms emphasize their role as embeddings, while homomorphisms illustrate flexible morphisms that respect underlying operations within categories.
Importance in Category Theory and Algebra
Monomorphisms are injective morphisms that preserve distinctness and play a crucial role in identifying subobjects within categories, enabling the analysis of structure embedding in algebraic systems. Homomorphisms are structure-preserving maps between algebraic objects that ensure operations and relations are maintained, serving as fundamental tools for comparing and transferring properties across groups, rings, and modules. The distinction and interaction between monomorphisms and homomorphisms facilitate understanding of object equivalence, factorization systems, and categorical limits, which are central in abstract algebra and category theory.
Summary and Practical Implications
Monomorphism refers to an injective structure-preserving map that ensures distinct elements remain distinct, while homomorphism is a broader concept describing any structure-preserving map between algebraic structures. In practical applications, monomorphisms guarantee embedding one structure into another without loss of information, which is critical in database schema design and type theory. Homomorphisms enable simplification or transformation of structures, playing a key role in cryptography, coding theory, and abstract algebra for system analysis and problem-solving.
Monomorphism Infographic
 libterm.com
libterm.com