Measurable cardinals are a type of large cardinal with strong combinatorial properties that play a crucial role in set theory, particularly in the study of infinite cardinalities and their hierarchies. Their existence implies the presence of a non-trivial, k-additive, 0-1 valued measure, making them central to discussions on inner models and determinacy. Explore the rest of the article to understand how measurable cardinals influence modern mathematical logic and foundational theories.
Table of Comparison
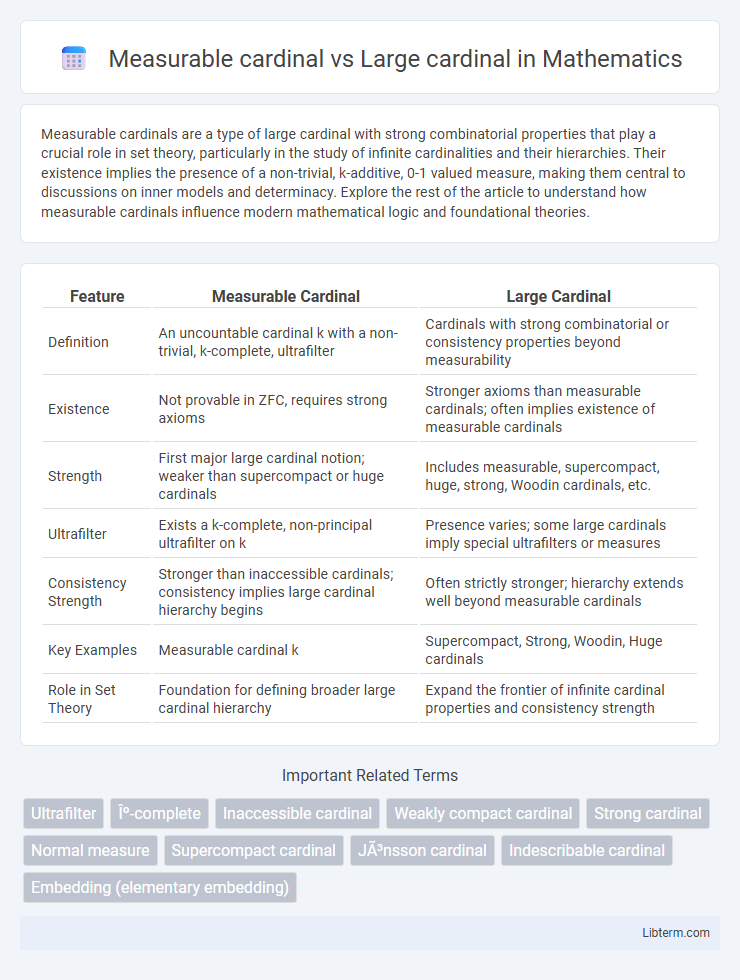
| Feature | Measurable Cardinal | Large Cardinal |
|---|---|---|
| Definition | An uncountable cardinal k with a non-trivial, k-complete, ultrafilter | Cardinals with strong combinatorial or consistency properties beyond measurability |
| Existence | Not provable in ZFC, requires strong axioms | Stronger axioms than measurable cardinals; often implies existence of measurable cardinals |
| Strength | First major large cardinal notion; weaker than supercompact or huge cardinals | Includes measurable, supercompact, huge, strong, Woodin cardinals, etc. |
| Ultrafilter | Exists a k-complete, non-principal ultrafilter on k | Presence varies; some large cardinals imply special ultrafilters or measures |
| Consistency Strength | Stronger than inaccessible cardinals; consistency implies large cardinal hierarchy begins | Often strictly stronger; hierarchy extends well beyond measurable cardinals |
| Key Examples | Measurable cardinal k | Supercompact, Strong, Woodin, Huge cardinals |
| Role in Set Theory | Foundation for defining broader large cardinal hierarchy | Expand the frontier of infinite cardinal properties and consistency strength |
Introduction to Large Cardinals
Large cardinals are a central concept in set theory, representing infinite sizes with extraordinary combinatorial and structural properties beyond standard infinite cardinals. Measurable cardinals form a fundamental subclass of large cardinals, characterized by the existence of a non-trivial, k-additive, 0-1-valued measure on the cardinal k. These cardinals indicate profound consistency strength and have substantial implications in areas such as descriptive set theory and the hierarchy of infinite sets.
Defining Measurable Cardinals
Measurable cardinals are a specific type of large cardinal characterized by the existence of a non-principal, k-additive, 0-1 valued measure on the power set of the cardinal k, known as a k-complete ultrafilter. This property ensures that measurable cardinals extend beyond the reach of smaller large cardinals like inaccessible cardinals, establishing a significant hierarchy in set theory. The presence of such a measure implies strong combinatorial and consistency strength, often used in the study of inner models and determinacy hypotheses.
Hierarchy of Large Cardinals
Measurable cardinals are a fundamental type within the hierarchy of large cardinals, characterized by the existence of a non-trivial, k-complete ultrafilter over the cardinal k. Large cardinals form an ascending hierarchy of increasingly strong axiomatic assumptions extending beyond ZFC, including inaccessible, Mahlo, measurable, and supercompact cardinals, each with distinct combinatorial and structural properties. The position of measurable cardinals in this hierarchy marks a significant threshold as the first large cardinal notion implying the existence of a non-principal ultrafilter, bridging the gap between smaller large cardinals like inaccessible cardinals and stronger notions such as supercompact cardinals.
Key Properties of Measurable Cardinals
Measurable cardinals are a specific type of large cardinal characterized by the existence of a non-trivial, k-additive, 0-1 valued measure over the cardinal k, called a measurable or k-complete ultrafilter. This measure allows for strong combinatorial and reflection properties, making measurable cardinals significant in set theory, especially in studying the structure of the universe of sets (V). Unlike some broader large cardinals, measurable cardinals provide a rich framework for defining elementary embeddings and have profound consistency strength implications.
Distinguishing Large and Measurable Cardinals
Measurable cardinals are a specific type of large cardinal characterized by the existence of a non-trivial, k-additive, 0-1-valued measure on the cardinal k, enabling the construction of ultrapowers and elementary embeddings. Large cardinals encompass a broader hierarchy of strong axioms in set theory, including inaccessible, Mahlo, measurable, strong, and supercompact cardinals, defined by various consistency strengths and combinatorial properties. The key distinction lies in measurability relying on the existence of a k-complete ultrafilter, while large cardinals may be defined through stronger elementary embedding properties or reflecting combinatorial principles beyond measure theory.
Historical Development of Cardinal Concepts
Measurable cardinals emerged as a pivotal concept in set theory during the mid-20th century, introduced by Dana Scott in the 1960s to explore large cardinal axioms extending beyond inaccessible cardinals. Large cardinals, encompassing a hierarchy including weakly compact, measurable, and supercompact cardinals, developed through progressive advances in understanding infinite set structures and consistency strength. The historical evolution reflects deepening insights into the nature of infinity, set-theoretic universes, and the foundational role of ultrafilters and elementary embeddings characterizing measurable cardinals within the large cardinal framework.
Consistency and Independence Results
Measurable cardinals are large cardinals characterized by the existence of a nontrivial, k-complete ultrafilter, providing a strong form of largeness that implies the failure of the axiom of constructibility (V L). Consistency strength of measurable cardinals surpasses that of many smaller large cardinals, and their existence cannot be proved within ZFC, making them a key tool in independence results related to determinacy and inner model theory. Large cardinals, including stronger notions like supercompact or strong cardinals, represent hierarchies of increasing consistency strength, with measurable cardinals serving as the foundational benchmark for many advanced independence proofs in set theory.
Impact on Set Theory and Mathematics
Measurable cardinals, a type of large cardinal characterized by the existence of a non-trivial, k-additive, 0-1-valued measure, have a profound impact on set theory by enabling the construction of models with rich combinatorial and structural properties that extend beyond ZFC axioms. Large cardinals broadly influence the foundations of mathematics, often implying the consistency strength of various set-theoretic hypotheses and fostering deeper insights into the hierarchy of infinite sizes and determinacy principles. The existence of measurable cardinals strengthens the power of inner model theory and descriptive set theory, revealing connections between large cardinal axioms and regularity properties of sets of reals.
Notable Theorems Involving Large Cardinals
Measurable cardinals are a type of large cardinal characterized by the existence of a non-trivial, k-complete ultrafilter, which leads to notable theorems such as the Kunen inconsistency, asserting no nontrivial elementary embedding of the universe holds, and the ultrapower construction producing fine structural models. Large cardinals, including inaccessible, Mahlo, and supercompact cardinals, feature prominently in results like Woodin's O-logic and the inner model theory, providing frameworks for understanding determinacy and descriptive set theory. These theorems reveal profound connections between set-theoretic hierarchies and foundational aspects of mathematics, highlighting the role of large cardinals in resolving consistency and independence problems.
Open Questions and Future Directions
Measurable cardinals, a specific type of large cardinal, possess a nontrivial, \(\kappa\)-additive, 0-1 valued measure, raising open questions about their exact consistency strength relative to other large cardinal axioms. Future research aims to clarify the fine structure of large cardinal hierarchies, explore the interplay between measurable cardinals and determinacy principles, and develop new forcing techniques to probe their combinatorial properties. Understanding these aspects is crucial for advancing set theory's foundational framework and resolving longstanding problems concerning cardinal hierarchies and inner model theory.
Measurable cardinal Infographic
 libterm.com
libterm.com