Functors are fundamental concepts in functional programming and category theory, representing mappings between categories that preserve structure. They enable you to apply functions over wrapped or context-filled data types like lists or options without altering the context itself. Explore the rest of the article to understand how functors simplify complex data transformations and enhance your code's composability.
Table of Comparison
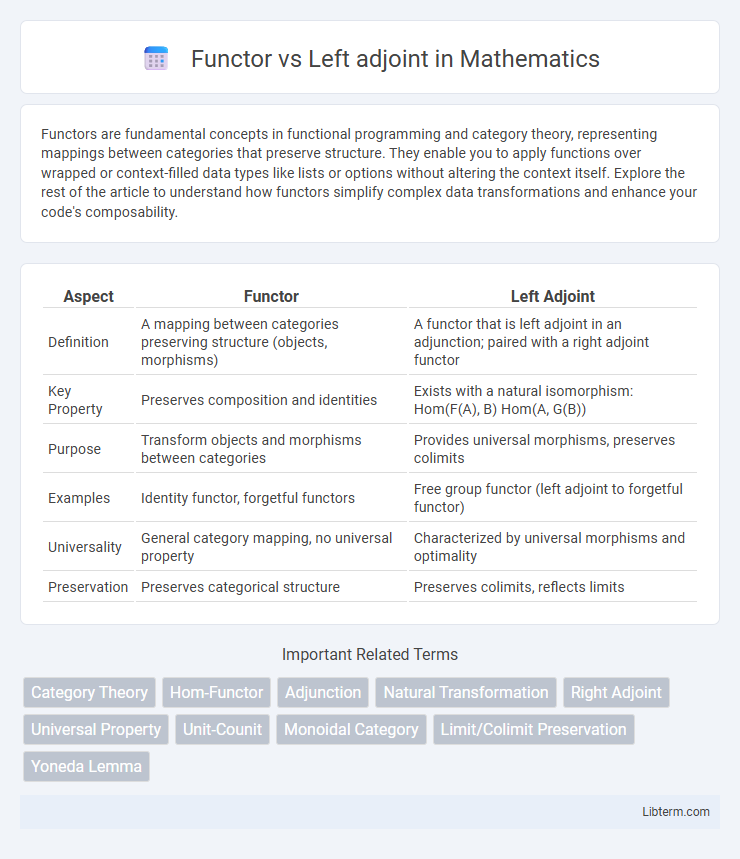
| Aspect | Functor | Left Adjoint |
|---|---|---|
| Definition | A mapping between categories preserving structure (objects, morphisms) | A functor that is left adjoint in an adjunction; paired with a right adjoint functor |
| Key Property | Preserves composition and identities | Exists with a natural isomorphism: Hom(F(A), B) Hom(A, G(B)) |
| Purpose | Transform objects and morphisms between categories | Provides universal morphisms, preserves colimits |
| Examples | Identity functor, forgetful functors | Free group functor (left adjoint to forgetful functor) |
| Universality | General category mapping, no universal property | Characterized by universal morphisms and optimality |
| Preservation | Preserves categorical structure | Preserves colimits, reflects limits |
Introduction to Functors and Left Adjoints
Functors are mappings between categories that preserve structures by assigning objects and morphisms from one category to another while maintaining composition and identity. Left adjoints arise in pairs with right adjoints, forming adjunctions that capture a generalized notion of "inverse" relationships between functors, often facilitating universal constructions. Understanding left adjoints involves examining how they provide the most efficient or "free" way to move between categories while preserving essential categorical properties.
Basic Definitions: Functor and Adjunction
A functor is a mapping between categories that preserves the structure of objects and morphisms, ensuring compositions and identities are maintained. A left adjoint functor is part of an adjunction, a pair of functors between two categories where one functor (left adjoint) is "best" at approximating inverses to the other (right adjoint) via a natural isomorphism between hom-sets. This adjunction captures a deep relationship enabling the transfer of structures and properties across categories in a way that generalizes universal constructions.
Understanding Functors: Structure-Preserving Maps
Functors are structure-preserving maps between categories that assign objects and morphisms in one category to objects and morphisms in another while maintaining composition and identity. Left adjoints are special functors that arise in adjunctions, characterized by a natural isomorphism between hom-sets, often preserving colimits and providing universal constructions. Understanding functors involves grasping how they transfer the categorical framework, while recognizing left adjoints highlights their role in creating optimal mappings with universal properties.
What is a Left Adjoint?
A left adjoint is a functor that pairs with a right adjoint functor, forming an adjunction characterized by a natural isomorphism between Hom-sets. It preserves colimits and provides universal constructions that map objects from one category into another most efficiently. Left adjoints are fundamental in category theory for modeling processes like free constructions and can be identified by the property that for each object in the target category, there is a universal morphism from its left adjoint image.
Key Differences: Functor vs Left Adjoint
A functor is a mapping between categories preserving structure, associating objects and morphisms in a way that respects composition and identities. A left adjoint functor specifically forms part of an adjunction, paired with a right adjoint functor, characterized by a natural isomorphism between hom-sets. Key differences include that every left adjoint functor is a functor with additional properties ensuring universal constructions, while not all functors serve as left adjoints.
Examples of Functors and Left Adjoints in Category Theory
Examples of functors include the forgetful functor from the category of groups to sets, which maps each group to its underlying set, and the free group functor from sets to groups, assigning each set the free group generated by it. The free group functor is a classic example of a left adjoint, left adjoint to the forgetful functor, demonstrating the adjunction property through natural isomorphisms between hom-sets. Another example is the tensor product functor in module categories, which is left adjoint to the Hom functor, illustrating the fundamental interplay between tensor and Hom constructions in category theory.
Role of Left Adjoints in Mathematical Structures
Left adjoint functors play a crucial role in mathematical structures by providing canonical ways to construct free objects that preserve colimits, such as free groups, free modules, or free algebras. They enable the translation of objects between categories while maintaining universal properties essential for defining limits and colimits. In category theory, left adjoints facilitate the embedding of simpler structures into more complex ones, ensuring the existence of optimal solutions to lifting problems and natural transformations.
Functors That Are Not Left Adjoints: Illustrative Cases
Functors that are not left adjoints often fail to preserve colimits or lack the necessary universal morphisms defining adjunctions, exhibiting behavior distinct from left adjoints known for their colimit preservation and universal properties. Examples include certain forgetful functors from algebraic categories that do not admit a left adjoint due to absence of free constructions or non-existence of initial objects in the target category. These cases highlight the importance of structural conditions and categorical properties governing whether a functor qualifies as a left adjoint, emphasizing that not all functors naturally fit into adjoint pairs.
Practical Applications: Functors and Left Adjoints
Functors enable practical applications by systematically mapping objects and morphisms between categories, essential in computer science for modeling type systems and data transformations. Left adjoint functors provide universal constructions, crucial in algebraic topology and category theory for building free objects and solving optimization problems. Their interplay facilitates efficient modular design in programming languages and formal verification methods.
Summary and Further Reading
Functors serve as mappings between categories, preserving structures through objects and morphisms, while left adjoints arise as functors that uniquely correspond with right adjoints via natural isomorphisms of hom-sets, reflecting a fundamental duality in category theory. Understanding the relationship between functors and left adjoints is crucial for exploring universal constructions, limits, and colimits, which underpin many areas in mathematics and theoretical computer science. For further reading, consult "Categories for the Working Mathematician" by Saunders Mac Lane and "Category Theory" by Steve Awodey for comprehensive treatments of adjoint functors and their applications.
Functor Infographic
 libterm.com
libterm.com