Simply connected spaces are topological spaces without any holes, meaning every loop within the space can be continuously contracted to a single point. This property is fundamental in complex analysis and algebraic topology, influencing how functions behave on these surfaces. Explore the rest of the article to understand how simply connected spaces impact various mathematical theories and applications.
Table of Comparison
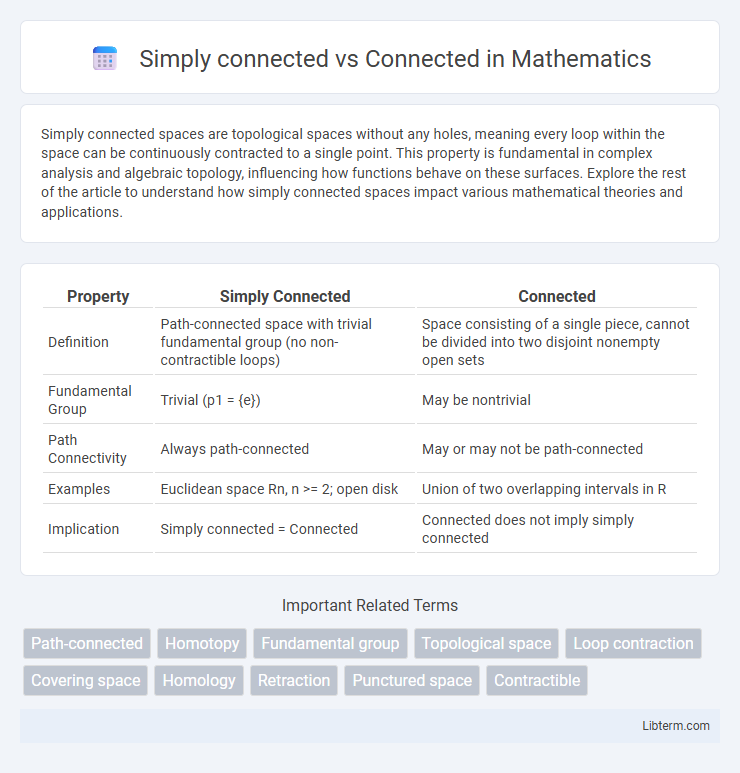
| Property | Simply Connected | Connected |
|---|---|---|
| Definition | Path-connected space with trivial fundamental group (no non-contractible loops) | Space consisting of a single piece, cannot be divided into two disjoint nonempty open sets |
| Fundamental Group | Trivial (p1 = {e}) | May be nontrivial |
| Path Connectivity | Always path-connected | May or may not be path-connected |
| Examples | Euclidean space Rn, n >= 2; open disk | Union of two overlapping intervals in R |
| Implication | Simply connected = Connected | Connected does not imply simply connected |
Understanding Topological Spaces
Simply connected spaces are a subset of connected topological spaces characterized by the absence of any holes, meaning every loop can be continuously contracted to a single point within the space. Connected spaces only require that the space be a single piece without separation, allowing for more complex structures like loops that cannot be contracted. Understanding the distinction between simply connected and connected spaces is crucial in topology, as it impacts properties such as path-connectedness, fundamental groups, and the types of continuous mappings that can exist.
Defining Connected Spaces
Connected spaces in topology are defined as those that cannot be partitioned into two disjoint nonempty open sets, reflecting an unbroken and continuous structure. Simply connected spaces are a subset of connected spaces characterized by the absence of holes, meaning every loop can be contracted to a point within the space. This distinction highlights that while all simply connected spaces are connected, not all connected spaces are simply connected.
What Does Simply Connected Mean?
Simply connected spaces are topological spaces without holes, meaning any loop within the space can be continuously contracted to a single point. Connected spaces, by contrast, only require that the space be in one piece, allowing loops that may not be contractible due to the presence of holes or obstacles. The concept of simply connectedness is crucial in fields like complex analysis and algebraic topology, where it ensures the existence of unique analytic continuations and trivial fundamental groups.
Key Differences: Connected vs. Simply Connected
Connected spaces in topology are those that cannot be divided into two disjoint nonempty open sets, ensuring a single piece or component. Simply connected spaces have the additional property that every loop within the space can be continuously contracted to a single point, meaning no holes or obstacles prevent such deformation. The key difference lies in simple connectedness requiring both connectedness and the absence of holes, making simply connected spaces a subset of connected spaces with stronger topological constraints.
Visualizing Concepts with Example Shapes
Simply connected spaces have no holes, meaning any loop within the shape can be continuously contracted to a point, such as a solid disk. Connected spaces ensure a path exists between any two points but can contain holes, like a doughnut-shaped torus, which is connected but not simply connected. Visualizing these concepts helps distinguish a coffee cup (with a handle) as simply connected only if the handle is filled in, otherwise it resembles a torus, demonstrating connectivity with holes.
Real-World Applications of Connectedness
Connected spaces in topology allow for continuous paths between any two points, crucial for network design and geographic information systems that require uninterrupted data flow or navigation routes. Simply connected spaces, which have no holes or loops, are essential in robotics for path planning, ensuring that a robot can move from one point to another without encountering obstacles that cannot be bypassed. Practical applications include electromagnetic field analysis and fluid dynamics, where simply connected domains simplify calculations and improve modeling accuracy.
Common Misconceptions Clarified
Simply connected spaces are often mistaken as just connected spaces, but the key difference is that simply connected spaces have no holes or loops, ensuring every loop can be continuously contracted to a point. Connected spaces only require a path between any two points, without restrictions on topological holes or loops. Common misconceptions confuse connectivity with simple connectivity, overlooking that all simply connected spaces are connected, but not all connected spaces are simply connected.
The Role of Holes and Paths
Simply connected spaces have no holes, ensuring every loop can be continuously contracted to a point, while connected spaces only require that any two points can be joined by a path without necessarily having contractible loops. The presence of holes obstructs the contraction of loops, making the space connected but not simply connected. The fundamental group captures these differences by encoding the equivalence classes of loops, distinguishing simply connected spaces with a trivial fundamental group from connected spaces with nontrivial groups due to holes.
Practical Tests for Connectedness
Practical tests for connectedness in topology often involve verifying that any two points in a space can be joined by a continuous path, confirming the space is path-connected and hence connected. Simply connected spaces require all loops to be contractible to a point, which is typically tested using tools like the fundamental group or homotopy techniques. For practical applications, connectedness tests focus on path existence, while simply connectedness demands analysis of loop contraction properties.
Summary Table: Connected vs. Simply Connected
Connected spaces are those in which any two points can be joined by a path, indicating there are no isolated parts, while simply connected spaces have no holes, meaning every loop can be continuously contracted to a point. The summary table comparing connected and simply connected spaces highlights that all simply connected spaces are connected, but not all connected spaces are simply connected, as the latter requires higher topological constraints. Key examples include the circle, which is connected but not simply connected, and the disk, which is both connected and simply connected, illustrating the fundamental distinction in topological properties.
Simply connected Infographic
 libterm.com
libterm.com